Template:Loglogistic distribution characteristics

Distribution Characteristics

For [math]\displaystyle{ \sigma \gt 1 }[/math] :

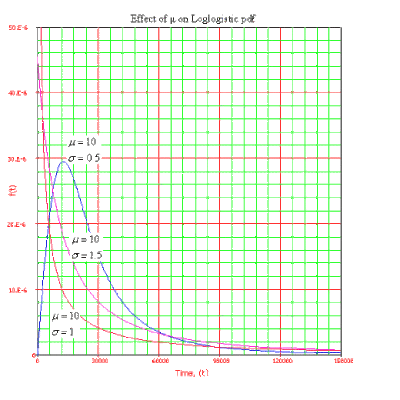
• [math]\displaystyle{ f(T) }[/math] decreases monotonically and is convex. Mode and mean do not exist.

For [math]\displaystyle{ \sigma =1 }[/math] :

• [math]\displaystyle{ f(T) }[/math] decreases monotonically and is convex. Mode and mean do not exist. As [math]\displaystyle{ T\to 0 }[/math] , [math]\displaystyle{ f(T)\to \tfrac{1}{\sigma {{e}^{\tfrac{\mu }{\sigma }}}}. }[/math]

• As [math]\displaystyle{ T\to 0 }[/math] , [math]\displaystyle{ \lambda (T)\to \tfrac{1}{\sigma {{e}^{\tfrac{\mu }{\sigma }}}}. }[/math]

For [math]\displaystyle{ 0\lt \sigma \lt 1 }[/math] :

• The shape of the loglogistic distribution is very similar to that of the lognormal distribution and the Weibull distribution.

• The [math]\displaystyle{ pdf }[/math] starts at zero, increases to its mode, and decreases thereafter.

• As [math]\displaystyle{ \mu }[/math] increases, while [math]\displaystyle{ \sigma }[/math] is kept the same, the [math]\displaystyle{ pdf }[/math] gets stretched out to the right and its height decreases, while maintaining its shape.

• As [math]\displaystyle{ \mu }[/math] decreases,while [math]\displaystyle{ \sigma }[/math] is kept the same, the .. gets pushed in towards the left and its height increases.

• [math]\displaystyle{ \lambda (T) }[/math] increases till [math]\displaystyle{ T={{e}^{\mu +\sigma \ln (\tfrac{1-\sigma }{\sigma })}} }[/math] and decreases thereafter. [math]\displaystyle{ \lambda (T) }[/math] is concave at first, then becomes convex.