Template:Rank Regression on X for Exponential Distribution

Rank Regression on X for Exponential Distribution

Similar to rank regression on Y, performing a rank regression on X requires that a straight line be fitted to a set of data points such that the sum of the squares of the horizontal deviations from the points to the line is minimized.

Again the first task is to bring our exponential [math]\displaystyle{ cdf }[/math] function into a linear form. This step is exactly the same as in regression on Y analysis. The deviation from the previous analysis begins on the least squares fit step, since in this case we treat [math]\displaystyle{ x }[/math] as the dependent variable and [math]\displaystyle{ y }[/math] as the independent variable. The best-fitting straight line to the data, for regression on X (see Chapter 4), is the straight line:

[math]\displaystyle{ x=\hat{a}+\hat{b}y }[/math]

The corresponding equations for [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math] are:

[math]\displaystyle{ \hat{a}=\overline{x}-\hat{b}\overline{y}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N} }[/math]

and:

[math]\displaystyle{ \hat{b}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}{{y}_{i}}-\tfrac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}}{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,y_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}} \right)}^{2}}}{N}} }[/math]

where:

[math]\displaystyle{ {{y}_{i}}=\ln [1-F({{t}_{i}})] }[/math]

and:

[math]\displaystyle{ {{x}_{i}}={{t}_{i}} }[/math]

The values of [math]\displaystyle{ F({{t}_{i}}) }[/math] are estimated from the median ranks. Once [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math] are obtained, solve for the unknown [math]\displaystyle{ y }[/math] value, which corresponds to:

[math]\displaystyle{ y=-\frac{\hat{a}}{\hat{b}}+\frac{1}{\hat{b}}x }[/math]

Solving for the parameters from above equations we get:

[math]\displaystyle{ a=-\frac{\hat{a}}{\hat{b}}=\lambda \gamma \Rightarrow \gamma =\hat{a} }[/math]

and:

[math]\displaystyle{ b=\frac{1}{\hat{b}}=-\lambda \Rightarrow \lambda =-\frac{1}{\hat{b}} }[/math]

For the one-parameter exponential case, equations for estimating a and b become:

[math]\displaystyle{ \begin{align} \hat{a}= & 0 \\ \hat{b}= & \frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}{{y}_{i}}}{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,y_{i}^{2}} \end{align} }[/math]

The correlation coefficient is evaluated as before.

Example 3: 2 Parameter Exponential Distribution RRX

Using the data of Example 2 and assuming a two-parameter exponential distribution, estimate the parameters and determine the correlation coefficient estimate, [math]\displaystyle{ \hat{\rho } }[/math], using rank regression on X.

Solution to Example 3

Table 7.2 constructed in Example 2 applies to this example also. Using the values from this table, we get:

[math]\displaystyle{ \begin{align} \hat{b}= & \frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}}{{y}_{i}}-\tfrac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}}\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}}}{14}}{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,y_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}} \right)}^{2}}}{14}} \\ \\ \hat{b}= & \frac{-927.4899-(630)(-13.2315)/14}{22.1148-{{(-13.2315)}^{2}}/14} \end{align} }[/math]

or:

[math]\displaystyle{ \hat{b}=-34.5563 }[/math]

and:

[math]\displaystyle{ \hat{a}=\overline{x}-\hat{b}\overline{y}=\frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}}}{14}-\hat{b}\frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}}}{14} }[/math]

or:

[math]\displaystyle{ \hat{a}=\frac{630}{14}-(-34.5563)\frac{(-13.2315)}{14}=12.3406 }[/math]

Therefore:

[math]\displaystyle{ \hat{\lambda }=-\frac{1}{\hat{b}}=-\frac{1}{(-34.5563)}=0.0289\text{ failures/hour} }[/math]

and:

[math]\displaystyle{ \hat{\gamma }=\hat{a}=12.3406 }[/math]

The correlation coefficient is found to be:

[math]\displaystyle{ \hat{\rho }=-0.9679 }[/math]

Note that the equation for regression on Y is not necessarily the same as that for the regression on X. The only time when the two regression methods yield identical results is when the data lie perfectly on a line. If this were the case, the correlation coefficient would be [math]\displaystyle{ -1 }[/math]. The negative value of the correlation coefficient is due to the fact that the slope of the exponential probability plot is negative.

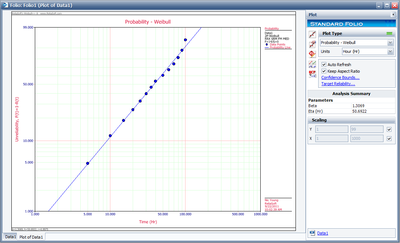
This example can be repeated using Weibull++, choosing two-parameter exponential and rank regression on X (RRX) methods for analysis, as shown below. The estimated parameters and the correlation coefficient using Weibull++ were found to be:

[math]\displaystyle{ \begin{array}{*{35}{l}} \hat{\lambda }= &0.0289 \text{failures/hour} \\ \hat{\gamma}= & 12.3395 \text{hours} \\ \hat{\rho} = &-0.9679 \\ \end{array} }[/math]

The probability plot can be obtained simply by clicking the Plot icon.