Template:Alta exponential distribution
The Exponential Distribution
The exponential distribution is a very commonly used distribution in reliability engineering. Due to its simplicity, it has been widely employed even in cases to which it does not apply. The exponential distribution is used to describe units that have a constant failure rate.
The single-parameter exponential [math]\displaystyle{ pdf }[/math] is given by:
- [math]\displaystyle{ \begin{align} & f(T)= & \lambda {{e}^{-\lambda T}}=\frac{1}{m}{{e}^{-\tfrac{1}{m}T}} \\ & T\ge & 0,\lambda \gt 0,m\gt 0 \end{align} }[/math]
- where:
- • [math]\displaystyle{ \lambda = }[/math] constant failure rate, in failures per unit of measurement, e.g. failures per hour, per cycle, etc.
- • [math]\displaystyle{ \lambda =\tfrac{1}{m}. }[/math]
- • [math]\displaystyle{ m= }[/math] mean time between failures, or to a failure.
- • [math]\displaystyle{ T= }[/math] operating time, life, or age, in hours, cycles, miles, actuations, etc.
This distribution requires the estimation of only one parameter, [math]\displaystyle{ \lambda }[/math] , for its application.
Statistical Properties Summary
The Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \mathop{}_{0}^{\infty }t\cdot f(t)dt=\mathop{}_{0}^{\infty }t\cdot \lambda \cdot {{e}^{-\lambda t}}dt \\ & = & \frac{1}{\lambda } \end{align} }[/math]
The Median
The median, [math]\displaystyle{ \breve{T} }[/math],
of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ \breve{T}=\frac{1}{\lambda }0.693 }[/math]
The Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math]
of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ \tilde{T}=0 }[/math]
The Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math] , of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{\lambda }=m }[/math]
The Reliability Function
The 1-parameter exponential reliability function is given by:
- [math]\displaystyle{ R(T)={{e}^{-\lambda T}}={{e}^{-\tfrac{T}{m}}} }[/math]
This function is the complement of the exponential cumulative distribution function or:
- [math]\displaystyle{ R(T)=1-Q(T)=1-\mathop{}_{0}^{T}f(T)dT }[/math]
- and:
- [math]\displaystyle{ R(T)=1-\mathop{}_{0}^{T}\lambda {{e}^{-\lambda T}}dT={{e}^{-\lambda T}} }[/math]
Conditional Reliability
The conditional reliability function for the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ R(T,t)=\frac{R(T+t)}{R(T)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\lambda t}} }[/math]
which says that the reliability for a mission of [math]\displaystyle{ t }[/math] duration undertaken after the component or equipment has already accumulated [math]\displaystyle{ T }[/math] hours of operation from age zero is only a function of the mission duration, and not a function of the age at the beginning of the mission. This is referred to as the ``memoryless property.
Reliable Life
The reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}} }[/math] , for the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ \begin{align} & R({{t}_{R}})= & {{e}^{-\lambda {{t}_{R}}}} \\ & & \\ & \ln [R({{t}_{R}})]= & -\lambda {{t}_{R}} \end{align} }[/math]
- or:
- [math]\displaystyle{ {{t}_{R}}=-\frac{\ln [R({{t}_{R}})]}{\lambda } }[/math]
Failure Rate Function
The exponential failure rate function is given by:
- [math]\displaystyle{ \lambda (T)=\frac{f(T)}{R(T)}=\frac{\lambda {{e}^{-\lambda (T)}}}{{{e}^{-\lambda (T)}}}=\lambda =\text{Constant} }[/math]
Characteristics
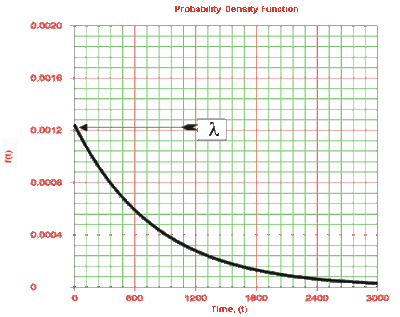
The characteristics of the 1-parameter exponential distribution can be exemplified by examining its parameter, lambda, [math]\displaystyle{ \lambda , }[/math] and the effect lambda has on the [math]\displaystyle{ pdf }[/math] , reliability and failure rate functions.
Effects of [math]\displaystyle{ \lambda }[/math] on the pdf
- • The scale parameter is [math]\displaystyle{ \tfrac{1}{\lambda } }[/math] .
- • As [math]\displaystyle{ \lambda }[/math] is decreased in value, the distribution is stretched out to the right, and as [math]\displaystyle{ \lambda }[/math] is increased, the distribution is pushed toward the origin.
- • This distribution has no shape parameter as it has only one shape, i.e. the exponential. The only parameter it has is the failure rate, [math]\displaystyle{ \lambda }[/math] .
- • The distribution starts at [math]\displaystyle{ T=0 }[/math] at the level of [math]\displaystyle{ f(T=0)=\lambda }[/math] and decreases thereafter exponentially and monotonically as [math]\displaystyle{ T }[/math] increases, and is convex.
- • As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ f(T)\to 0 }[/math].
- • This [math]\displaystyle{ pdf }[/math] can be thought of as a special case of the Weibull [math]\displaystyle{ pdf }[/math] with [math]\displaystyle{ \beta =1 }[/math] .
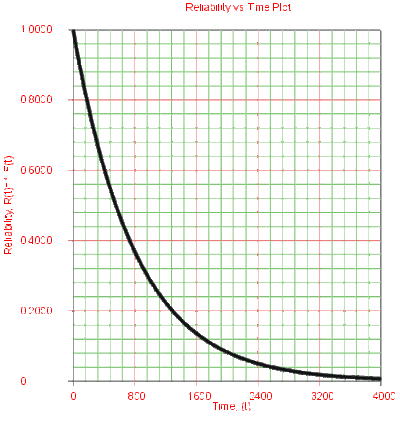
Effects of [math]\displaystyle{ \lambda }[/math] on the Reliability Function
- • The 1-parameter exponential reliability function starts at the value of 1 at [math]\displaystyle{ T=0 }[/math] . It decreases thereafter monotonically and is convex.
- • As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ R(T\to \infty )\to 0 }[/math].
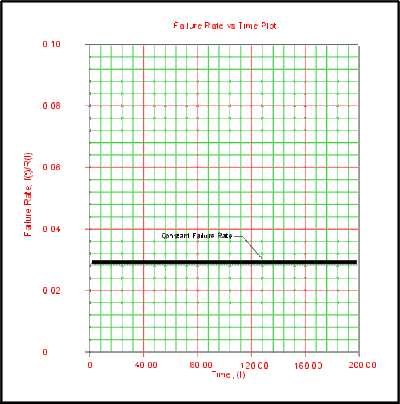
Effects of [math]\displaystyle{ \lambda }[/math] on the Failure Rate Function
The failure rate function for the exponential distribution is constant and it is equal to the parameter [math]\displaystyle{ \lambda }[/math] .