Confidence Bounds

Confidence Bounds

What are Confidence Bounds?

One of the most confusing concepts to a novice reliability engineer is estimating the precision of an estimate. This is an important concept in the field of reliability engineering, leading to the use of confidence intervals (or bounds). In this section, we will try to briefly present the concept in relatively simple terms but based on solid common sense.

The Black and White Marbles

To illustrate, consider the case where there are millions of perfectly mixed black and white marbles in a rather large swimming pool and our job is to estimate the percentage of black marbles. The only way to be absolutely certain about the exact percentage of marbles in the pool is to accurately count every last marble and calculate the percentage. However, this is too time- and resource-intensive to be a viable option, so we need to come up with a way of estimating the percentage of black marbles in the pool. In order to do this, we would take a relatively small sample of marbles from the pool and then count how many black marbles are in the sample.

Taking a Small Sample of Marbles

First, pick out a small sample of marbles and count the black ones. Say you picked out ten marbles and counted four black marbles. Based on this, your estimate would be that 40% of the marbles are black.

If you put the ten marbles back in the pool and repeat this example again, you might get six black marbles, changing your estimate to 60% black marbles. Which of the two is correct? Both estimates are correct! As you repeat this experiment over and over again, you might find out that this estimate is usually between [math]\displaystyle{ {{X}_{1}}% }[/math] and [math]\displaystyle{ {{X}_{2}}% }[/math], and you can assign a percentage to the number of times your estimate falls between these limits. For example, you notice that 90% of the time this estimate is between [math]\displaystyle{ {{X}_{1}}% }[/math] and [math]\displaystyle{ {{X}_{2}}%. }[/math]

Taking a Larger Sample of Marbles

If you now repeat the experiment and pick out 1,000 marbles, you might get results for the number of black marbles such as 545, 570, 530, etc., for each trial. The range of the estimates in this case will be much narrower than before. For example, you observe that 90% of the time, the number of black marbles will now be from [math]\displaystyle{ {{Y}_{1}}% }[/math] to [math]\displaystyle{ {{Y}_{2}}% }[/math], where [math]\displaystyle{ {{X}_{1}}%\lt {{Y}_{1}}% }[/math] and [math]\displaystyle{ {{X}_{2}}%\gt {{Y}_{2}}% }[/math], thus giving you a more narrow estimate interval. The same principle is true for confidence intervals; the larger the sample size, the more narrow the confidence intervals.

Back to Reliability

We will now look at how this phenomenon relates to reliability. Overall, the reliability engineer's task is to determine the probability of failure, or reliability, of the population of units in question. However, one will never know the exact reliability value of the population unless one is able to obtain and analyze the failure data for every single unit in the population. Since this usually is not a realistic situation, the task then is to estimate the reliability based on a sample, much like estimating the number of black marbles in the pool. If we perform ten different reliability tests for our units, and analyze the results, we will obtain slightly different parameters for the distribution each time, and thus slightly different reliability results. However, by employing confidence bounds, we obtain a range within which these reliability values are likely to occur a certain percentage of the time. This helps us gauge the utility of the data and the accuracy of the resulting estimates. Plus, it is always useful to remember that each parameter is an estimate of the true parameter, one that is unknown to us. This range of plausible values is called a confidence interval.

One-Sided and Two-Sided Confidence Bounds

Confidence bounds are generally described as being one-sided or two-sided.

Two-Sided Bounds

When we use two-sided confidence bounds (or intervals), we are looking at a closed interval where a certain percentage of the population is likely to lie. That is, we determine the values, or bounds, between which lies a specified percentage of the population. For example, when dealing with 90% two-sided confidence bounds of [math]\displaystyle{ (X,Y) }[/math], we are saying that 90% of the population lies between [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] with 5% less than [math]\displaystyle{ X }[/math] and 5% greater than [math]\displaystyle{ Y }[/math].

One-Sided Bounds

One-sided confidence bounds are essentially an open-ended version of two-sided bounds. A one-sided bound defines the point where a certain percentage of the population is either higher or lower than the defined point. This means that there are two types of one-sided bounds: upper and lower. An upper one-sided bound defines a point that a certain percentage of the population is less than. Conversely, a lower one-sided bound defines a point that a specified percentage of the population is greater than.

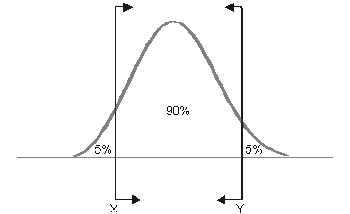
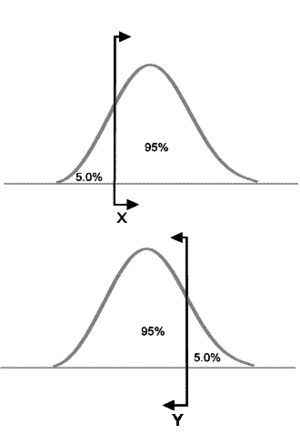
For example, if [math]\displaystyle{ X }[/math] is a 95% upper one-sided bound, this would imply that 95% of the population is less than [math]\displaystyle{ X }[/math]. If [math]\displaystyle{ X }[/math] is a 95% lower one-sided bound, this would indicate that 95% of the population is greater than [math]\displaystyle{ X }[/math]. Care must be taken to differentiate between one- and two-sided confidence bounds, as these bounds can take on identical values at different percentage levels. For example, in the figures above, we see bounds on a hypothetical distribution. Assuming this is the same distribution in all of the figures, we see that [math]\displaystyle{ X }[/math] marks the spot below which 5% of the distribution's population lies. Similarly, [math]\displaystyle{ Y }[/math] represents the point above which 5% of the population lies. Therefore, [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] represent the 90% two-sided bounds, since 90% of the population lies between the two points. However, [math]\displaystyle{ X }[/math] also represents the lower one-sided 95% confidence bound, since 95% of the population lies above that point; and [math]\displaystyle{ Y }[/math] represents the upper one-sided 95% confidence bound, since 95% of the population is below [math]\displaystyle{ Y }[/math]. It is important to be sure of the type of bounds you are dealing with, particularly as both one-sided bounds can be displayed simultaneously in Weibull++. In Weibull++, we use upper to represent the higher limit and lower to represent the lower limit, regardless of their position, but based on the value of the results. So if obtaining the confidence bounds on the reliability, we would identify the lower value of reliability as the lower limit and the higher value of reliability as the higher limit. If obtaining the confidence bounds on probability of failure we will again identify the lower numeric value for the probability of failure as the lower limit and the higher value as the higher limit.

Confidence Bounds

What are Confidence Bounds?

One of the most confusing concepts to a novice reliability engineer is estimating the precision of an estimate. This is an important concept in the field of reliability engineering, leading to the use of confidence intervals (or bounds). In this section, we will try to briefly present the concept in relatively simple terms but based on solid common sense.

The Black and White Marbles

To illustrate, consider the case where there are millions of perfectly mixed black and white marbles in a rather large swimming pool and our job is to estimate the percentage of black marbles. The only way to be absolutely certain about the exact percentage of marbles in the pool is to accurately count every last marble and calculate the percentage. However, this is too time- and resource-intensive to be a viable option, so we need to come up with a way of estimating the percentage of black marbles in the pool. In order to do this, we would take a relatively small sample of marbles from the pool and then count how many black marbles are in the sample.

Taking a Small Sample of Marbles

First, pick out a small sample of marbles and count the black ones. Say you picked out ten marbles and counted four black marbles. Based on this, your estimate would be that 40% of the marbles are black.

If you put the ten marbles back in the pool and repeat this example again, you might get six black marbles, changing your estimate to 60% black marbles. Which of the two is correct? Both estimates are correct! As you repeat this experiment over and over again, you might find out that this estimate is usually between [math]\displaystyle{ {{X}_{1}}% }[/math] and [math]\displaystyle{ {{X}_{2}}% }[/math], and you can assign a percentage to the number of times your estimate falls between these limits. For example, you notice that 90% of the time this estimate is between [math]\displaystyle{ {{X}_{1}}% }[/math] and [math]\displaystyle{ {{X}_{2}}%. }[/math]

Taking a Larger Sample of Marbles

If you now repeat the experiment and pick out 1,000 marbles, you might get results for the number of black marbles such as 545, 570, 530, etc., for each trial. The range of the estimates in this case will be much narrower than before. For example, you observe that 90% of the time, the number of black marbles will now be from [math]\displaystyle{ {{Y}_{1}}% }[/math] to [math]\displaystyle{ {{Y}_{2}}% }[/math], where [math]\displaystyle{ {{X}_{1}}%\lt {{Y}_{1}}% }[/math] and [math]\displaystyle{ {{X}_{2}}%\gt {{Y}_{2}}% }[/math], thus giving you a more narrow estimate interval. The same principle is true for confidence intervals; the larger the sample size, the more narrow the confidence intervals.

Back to Reliability

We will now look at how this phenomenon relates to reliability. Overall, the reliability engineer's task is to determine the probability of failure, or reliability, of the population of units in question. However, one will never know the exact reliability value of the population unless one is able to obtain and analyze the failure data for every single unit in the population. Since this usually is not a realistic situation, the task then is to estimate the reliability based on a sample, much like estimating the number of black marbles in the pool. If we perform ten different reliability tests for our units, and analyze the results, we will obtain slightly different parameters for the distribution each time, and thus slightly different reliability results. However, by employing confidence bounds, we obtain a range within which these reliability values are likely to occur a certain percentage of the time. This helps us gauge the utility of the data and the accuracy of the resulting estimates. Plus, it is always useful to remember that each parameter is an estimate of the true parameter, one that is unknown to us. This range of plausible values is called a confidence interval.

One-Sided and Two-Sided Confidence Bounds

Confidence bounds are generally described as being one-sided or two-sided.

Two-Sided Bounds

When we use two-sided confidence bounds (or intervals), we are looking at a closed interval where a certain percentage of the population is likely to lie. That is, we determine the values, or bounds, between which lies a specified percentage of the population. For example, when dealing with 90% two-sided confidence bounds of [math]\displaystyle{ (X,Y) }[/math], we are saying that 90% of the population lies between [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] with 5% less than [math]\displaystyle{ X }[/math] and 5% greater than [math]\displaystyle{ Y }[/math].

One-Sided Bounds

One-sided confidence bounds are essentially an open-ended version of two-sided bounds. A one-sided bound defines the point where a certain percentage of the population is either higher or lower than the defined point. This means that there are two types of one-sided bounds: upper and lower. An upper one-sided bound defines a point that a certain percentage of the population is less than. Conversely, a lower one-sided bound defines a point that a specified percentage of the population is greater than.

For example, if [math]\displaystyle{ X }[/math] is a 95% upper one-sided bound, this would imply that 95% of the population is less than [math]\displaystyle{ X }[/math]. If [math]\displaystyle{ X }[/math] is a 95% lower one-sided bound, this would indicate that 95% of the population is greater than [math]\displaystyle{ X }[/math]. Care must be taken to differentiate between one- and two-sided confidence bounds, as these bounds can take on identical values at different percentage levels. For example, in the figures above, we see bounds on a hypothetical distribution. Assuming this is the same distribution in all of the figures, we see that [math]\displaystyle{ X }[/math] marks the spot below which 5% of the distribution's population lies. Similarly, [math]\displaystyle{ Y }[/math] represents the point above which 5% of the population lies. Therefore, [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] represent the 90% two-sided bounds, since 90% of the population lies between the two points. However, [math]\displaystyle{ X }[/math] also represents the lower one-sided 95% confidence bound, since 95% of the population lies above that point; and [math]\displaystyle{ Y }[/math] represents the upper one-sided 95% confidence bound, since 95% of the population is below [math]\displaystyle{ Y }[/math]. It is important to be sure of the type of bounds you are dealing with, particularly as both one-sided bounds can be displayed simultaneously in Weibull++. In Weibull++, we use upper to represent the higher limit and lower to represent the lower limit, regardless of their position, but based on the value of the results. So if obtaining the confidence bounds on the reliability, we would identify the lower value of reliability as the lower limit and the higher value of reliability as the higher limit. If obtaining the confidence bounds on probability of failure we will again identify the lower numeric value for the probability of failure as the lower limit and the higher value as the higher limit.

Fisher Matrix Confidence Bounds

This section presents an overview of the theory on obtaining approximate confidence bounds on suspended (multiply censored) data. The methodology used is the so-called Fisher matrix bounds (FM), described in [[Nelson [30]]] and [[Lloyd and Lipow [24]]]. These bounds are employed in most other commercial statistical applications. In general, these bounds tend to be more optimistic than the non-parametric rank based bounds. This may be a concern, particularly when dealing with small sample sizes. Some statisticians feel that the Fisher matrix bounds are too optimistic when dealing with small sample sizes and prefer to use other techniques for calculating confidence bounds, such as the likelihood ratio bounds.

Approximate Estimates of the Mean and Variance of a Function

In utilizing FM bounds for functions, one must first determine the mean and variance of the function in question (i.e. reliability function, failure rate function, etc.). An example of the methodology and assumptions for an arbitrary function [math]\displaystyle{ G }[/math] is presented next.

Single Parameter Case

For simplicity, consider a one-parameter distribution represented by a general function, [math]\displaystyle{ G, }[/math] which is a function of one parameter estimator, say [math]\displaystyle{ G(\widehat{\theta }). }[/math] For example, the mean of the exponential distribution is a function of the parameter [math]\displaystyle{ \lambda }[/math]: [math]\displaystyle{ G(\lambda )=1/\lambda =\mu }[/math]. Then, in general, the expected value of [math]\displaystyle{ G\left( \widehat{\theta } \right) }[/math] can be found by:

[math]\displaystyle{ E\left( G\left( \widehat{\theta } \right) \right)=G(\theta )+O\left( \frac{1}{n} \right) }[/math]

where [math]\displaystyle{ G(\theta ) }[/math] is some function of [math]\displaystyle{ \theta }[/math], such as the reliability function, and [math]\displaystyle{ \theta }[/math] is the population parameter where [math]\displaystyle{ E\left( \widehat{\theta } \right)=\theta }[/math] as [math]\displaystyle{ n\to \infty }[/math] . The term [math]\displaystyle{ O\left( \tfrac{1}{n} \right) }[/math] is a function of [math]\displaystyle{ n }[/math], the sample size, and tends to zero, as fast as [math]\displaystyle{ \tfrac{1}{n}, }[/math] as [math]\displaystyle{ n\to \infty . }[/math] For example, in the case of [math]\displaystyle{ \widehat{\theta }=1/\overline{x} }[/math] and [math]\displaystyle{ G(x)=1/x }[/math], then [math]\displaystyle{ E(G(\widehat{\theta }))=\overline{x}+O\left( \tfrac{1}{n} \right) }[/math] where [math]\displaystyle{ O\left( \tfrac{1}{n} \right)=\tfrac{{{\sigma }^{2}}}{n} }[/math]. Thus as [math]\displaystyle{ n\to \infty }[/math], [math]\displaystyle{ E(G(\widehat{\theta }))=\mu }[/math] where [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \sigma }[/math] are the mean and standard deviation, respectively. Using the same one-parameter distribution, the variance of the function [math]\displaystyle{ G\left( \widehat{\theta } \right) }[/math] can then be estimated by:

[math]\displaystyle{ Var\left( G\left( \widehat{\theta } \right) \right)=\left( \frac{\partial G}{\partial \widehat{\theta }} \right)_{\widehat{\theta }=\theta }^{2}Var\left( \widehat{\theta } \right)+O\left( \frac{1}{{{n}^{\tfrac{3}{2}}}} \right) }[/math]

Two-Parameter Case

Consider a Weibull distribution with two parameters [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \eta }[/math]. For a given value of [math]\displaystyle{ T }[/math], [math]\displaystyle{ R(T)=G(\beta ,\eta )={{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}} }[/math]. Repeating the previous method for the case of a two-parameter distribution, it is generally true that for a function [math]\displaystyle{ G }[/math], which is a function of two parameter estimators, say [math]\displaystyle{ G\left( {{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}} \right) }[/math], that:

[math]\displaystyle{ E\left( G\left( {{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}} \right) \right)=G\left( {{\theta }_{1}},{{\theta }_{2}} \right)+O\left( \frac{1}{n} \right) }[/math]

and:

[math]\displaystyle{ \begin{align} Var( G( {{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}}))= &{(\frac{\partial G}{\partial {{\widehat{\theta }}_{1}}})^2}_{{\widehat{\theta_{1}}}={\theta_{1}}}Var(\widehat{\theta_{1}})+{(\frac{\partial G}{\partial {{\widehat{\theta }}_{2}}})^2}_{{\widehat{\theta_{2}}}={\theta_{1}}}Var(\widehat{\theta_{2}})\\ & +2{(\frac{\partial G}{\partial {{\widehat{\theta }}_{1}}})^2}_{{\widehat{\theta_{1}}}={\theta_{1}}}{(\frac{\partial G}{\partial {{\widehat{\theta }}_{2}}})^2}_{{\widehat{\theta_{2}}}={\theta_{1}}}Cov(\widehat{\theta_{1}},\widehat{\theta_{2}}) \\ & +O(\frac{1}{n^{\tfrac{3}{2}}}) \end{align} }[/math]

Note that the derivatives of Eqn. (var) are evaluated at [math]\displaystyle{ {{\widehat{\theta }}_{1}}={{\theta }_{1}} }[/math] and [math]\displaystyle{ {{\widehat{\theta }}_{2}}={{\theta }_{1}}, }[/math] where E [math]\displaystyle{ \left( {{\widehat{\theta }}_{1}} \right)\simeq {{\theta }_{1}} }[/math] and E [math]\displaystyle{ \left( {{\widehat{\theta }}_{2}} \right)\simeq {{\theta }_{2}}. }[/math]

Parameter Variance and Covariance Determination

The determination of the variance and covariance of the parameters is accomplished via the use of the Fisher information matrix. For a two-parameter distribution, and using maximum likelihood estimates (MLE), the log-likelihood function for censored data is given by:

[math]\displaystyle{ \begin{align} \ln [L]= & \Lambda =\underset{i=1}{\overset{R}{\mathop \sum }}\,\ln [f({{T}_{i}};{{\theta }_{1}},{{\theta }_{2}})] \\ & \text{ }+\underset{j=1}{\overset{M}{\mathop \sum }}\,\ln [1-F({{S}_{j}};{{\theta }_{1}},{{\theta }_{2}})] \\ & \text{ }+\underset{l=1}{\overset{P}{\mathop \sum }}\,\ln \left\{ F({{I}_{{{l}_{U}}}};{{\theta }_{1}},{{\theta }_{2}})-F({{I}_{{{l}_{L}}}};{{\theta }_{1}},{{\theta }_{2}}) \right\} \end{align} }[/math]

In the equation above, the first summation is for complete data, the second summation is for right censored data, and the third summation is for interval or left censored data. For more information on these data types, see Chapter 4.
Then the Fisher information matrix is given by:

[math]\displaystyle{ {{F}_{0}}=\left[ \begin{matrix} {{E}_{0}}{{\left[ -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{1}^{2}} \right]}_{0}} & {} & {{E}_{0}}{{\left[ -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{1}}\partial {{\theta }_{2}}} \right]}_{0}} \\ {} & {} & {} \\ {{E}_{0}}{{\left[ -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{2}}\partial {{\theta }_{1}}} \right]}_{0}} & {} & {{E}_{0}}{{\left[ -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{2}^{2}} \right]}_{0}} \\ \end{matrix} \right] }[/math]

The subscript [math]\displaystyle{ 0 }[/math] indicates that the quantity is evaluated at [math]\displaystyle{ {{\theta }_{1}}={{\theta }_{{{1}_{0}}}} }[/math] and [math]\displaystyle{ {{\theta }_{2}}={{\theta }_{{{2}_{0}}}}, }[/math] the true values of the parameters.
So for a sample of [math]\displaystyle{ N }[/math] units where [math]\displaystyle{ R }[/math] units have failed, [math]\displaystyle{ S }[/math] have been suspended, and [math]\displaystyle{ P }[/math] have failed within a time interval, and [math]\displaystyle{ N=R+M+P, }[/math] one could obtain the sample local information matrix by:

[math]\displaystyle{ F={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{1}^{2}} & {} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{1}}\partial {{\theta }_{2}}} \\ {} & {} & {} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{2}}\partial {{\theta }_{1}}} & {} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{2}^{2}} \\ \end{matrix} \right]}^{}} }[/math]

Substituting in the values of the estimated parameters, in this case [math]\displaystyle{ {{\widehat{\theta }}_{1}} }[/math] and [math]\displaystyle{ {{\widehat{\theta }}_{2}} }[/math], and then inverting the matrix, one can then obtain the local estimate of the covariance matrix or:

[math]\displaystyle{ \left[ \begin{matrix} \widehat{Var}\left( {{\widehat{\theta }}_{1}} \right) & {} & \widehat{Cov}\left( {{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}} \right) \\ {} & {} & {} \\ \widehat{Cov}\left( {{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}} \right) & {} & \widehat{Var}\left( {{\widehat{\theta }}_{2}} \right) \\ \end{matrix} \right]={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{1}^{2}} & {} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{1}}\partial {{\theta }_{2}}} \\ {} & {} & {} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{2}}\partial {{\theta }_{1}}} & {} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{2}^{2}} \\ \end{matrix} \right]}^{-1}} }[/math]

Then the variance of a function ([math]\displaystyle{ Var(G) }[/math]) can be estimated using Eqn. (var). Values for the variance and covariance of the parameters are obtained from Eqn. (Fisher2). Once they have been obtained, the approximate confidence bounds on the function are given as:

[math]\displaystyle{ C{{B}_{R}}=E(G)\pm {{z}_{\alpha }}\sqrt{Var(G)} }[/math]

which is the estimated value plus or minus a certain number of standard deviations. We address finding [math]\displaystyle{ {{z}_{\alpha }} }[/math] next.

Approximate Confidence Intervals on the Parameters

In general, MLE estimates of the parameters are asymptotically normal, meaning for large sample sizes that a distribution of parameter estimates from the same population would be very close to the normal distribution. Thus if [math]\displaystyle{ \widehat{\theta } }[/math] is the MLE estimator for [math]\displaystyle{ \theta }[/math], in the case of a single parameter distribution, estimated from a large sample of [math]\displaystyle{ n }[/math] units and if:

[math]\displaystyle{ z\equiv \frac{\widehat{\theta }-\theta }{\sqrt{Var\left( \widehat{\theta } \right)}} }[/math]

then using the normal distribution of [math]\displaystyle{ z\ \ : }[/math]

[math]\displaystyle{ P\left( x\le z \right)\to \Phi \left( z \right)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{z}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt }[/math]

for large [math]\displaystyle{ n }[/math]. We now place confidence bounds on [math]\displaystyle{ \theta , }[/math] at some confidence level [math]\displaystyle{ \delta }[/math], bounded by the two end points [math]\displaystyle{ {{C}_{1}} }[/math] and [math]\displaystyle{ {{C}_{2}} }[/math] where:

[math]\displaystyle{ P\left( {{C}_{1}}\lt \theta \lt {{C}_{2}} \right)=\delta }[/math]

From Eqn. (e729):

[math]\displaystyle{ P\left( -{{K}_{\tfrac{1-\delta }{2}}}\lt \frac{\widehat{\theta }-\theta }{\sqrt{Var\left( \widehat{\theta } \right)}}\lt {{K}_{\tfrac{1-\delta }{2}}} \right)\simeq \delta }[/math]

where [math]\displaystyle{ {{K}_{\alpha }} }[/math] is defined by:

[math]\displaystyle{ \alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi \left( {{K}_{\alpha }} \right) }[/math]

Now by simplifying Eqn. (e731), one can obtain the approximate two-sided confidence bounds on the parameter [math]\displaystyle{ \theta , }[/math] at a confidence level [math]\displaystyle{ \delta , }[/math] or:

[math]\displaystyle{ \left( \widehat{\theta }-{{K}_{\tfrac{1-\delta }{2}}}\cdot \sqrt{Var\left( \widehat{\theta } \right)}\lt \theta \lt \widehat{\theta }+{{K}_{\tfrac{1-\delta }{2}}}\cdot \sqrt{Var\left( \widehat{\theta } \right)} \right) }[/math]

The upper one-sided bounds are given by:

[math]\displaystyle{ \theta \lt \widehat{\theta }+{{K}_{1-\delta }}\sqrt{Var(\widehat{\theta })} }[/math]

while the lower one-sided bounds are given by:

[math]\displaystyle{ \theta \gt \widehat{\theta }-{{K}_{1-\delta }}\sqrt{Var(\widehat{\theta })} }[/math]

If [math]\displaystyle{ \widehat{\theta } }[/math] must be positive, then [math]\displaystyle{ \ln \widehat{\theta } }[/math] is treated as normally distributed. The two-sided approximate confidence bounds on the parameter [math]\displaystyle{ \theta }[/math], at confidence level [math]\displaystyle{ \delta }[/math], then become:

[math]\displaystyle{ \begin{align} & {{\theta }_{U}}= & \widehat{\theta }\cdot {{e}^{\tfrac{{{K}_{\tfrac{1-\delta }{2}}}\sqrt{Var\left( \widehat{\theta } \right)}}{\widehat{\theta }}}}\text{ (Two-sided upper)} \\ & {{\theta }_{L}}= & \frac{\widehat{\theta }}{{{e}^{\tfrac{{{K}_{\tfrac{1-\delta }{2}}}\sqrt{Var\left( \widehat{\theta } \right)}}{\widehat{\theta }}}}}\text{ (Two-sided lower)} \end{align} }[/math]

The one-sided approximate confidence bounds on the parameter [math]\displaystyle{ \theta }[/math], at confidence level [math]\displaystyle{ \delta , }[/math] can be found from:

[math]\displaystyle{ \begin{align} & {{\theta }_{U}}= & \widehat{\theta }\cdot {{e}^{\tfrac{{{K}_{1-\delta }}\sqrt{Var\left( \widehat{\theta } \right)}}{\widehat{\theta }}}}\text{ (One-sided upper)} \\ & {{\theta }_{L}}= & \frac{\widehat{\theta }}{{{e}^{\tfrac{{{K}_{1-\delta }}\sqrt{Var\left( \widehat{\theta } \right)}}{\widehat{\theta }}}}}\text{ (One-sided lower)} \end{align} }[/math]

The same procedure can be extended for the case of a two or more parameter distribution. Lloyd and Lipow [24] further elaborate on this procedure.

Confidence Bounds on Time (Type 1)

Type 1 confidence bounds are confidence bounds around time for a given reliability. For example, when using the one-parameter exponential distribution, the corresponding time for a given exponential percentile (i.e. y-ordinate or unreliability, [math]\displaystyle{ Q=1-R) }[/math] is determined by solving the unreliability function for the time, [math]\displaystyle{ T }[/math], or:

[math]\displaystyle{ \begin{align}\widehat{T}(Q)= &-\frac{1}{\widehat{\lambda }} \ln (1-Q)= & -\frac{1}{\widehat{\lambda }}\ln (R) \end{align} }[/math]

Bounds on time (Type 1) return the confidence bounds around this time value by determining the confidence intervals around [math]\displaystyle{ \widehat{\lambda } }[/math] and substituting these values into Eqn. (cb). The bounds on [math]\displaystyle{ \widehat{\lambda } }[/math] were determined using Eqns. (cblmu) and (cblml), with its variance obtained from Eqn. (Fisher2). Note that the procedure is slightly more complicated for distributions with more than one parameter.

Confidence Bounds on Reliability (Type 2)

Type 2 confidence bounds are confidence bounds around reliability. For example, when using the two-parameter exponential distribution, the reliability function is:

[math]\displaystyle{ \widehat{R}(T)={{e}^{-\widehat{\lambda }\cdot T}} }[/math]

Reliability bounds (Type 2) return the confidence bounds by determining the confidence intervals around [math]\displaystyle{ \widehat{\lambda } }[/math] and substituting these values into Eqn. (cbr). The bounds on [math]\displaystyle{ \widehat{\lambda } }[/math] were determined using Eqns. (cblmu) and (cblml), with its variance obtained from Eqn. (Fisher2). Once again, the procedure is more complicated for distributions with more than one parameter.

Beta Binomial Confidence Bounds

Another less mathematically intensive method of calculating confidence bounds involves a procedure similar to that used in calculating median ranks (see Chapter 4). This is a non-parametric approach to confidence interval calculations that involves the use of rank tables and is commonly known as beta-binomial bounds (BB). By non-parametric, we mean that no underlying distribution is assumed. (Parametric implies that an underlying distribution, with parameters, is assumed.) In other words, this method can be used for any distribution, without having to make adjustments in the underlying equations based on the assumed distribution. Recall from the discussion on the median ranks that we used the binomial equation to compute the ranks at the 50% confidence level (or median ranks) by solving the cumulative binomial distribution for [math]\displaystyle{ Z }[/math] (rank for the [math]\displaystyle{ {{j}^{th}} }[/math] failure):

[math]\displaystyle{ P=\underset{k=j}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} N \\ k \\ \end{matrix} \right){{Z}^{k}}{{\left( 1-Z \right)}^{N-k}} }[/math]

where [math]\displaystyle{ N }[/math] is the sample size and [math]\displaystyle{ j }[/math] is the order number.
The median rank was obtained by solving the following equation for [math]\displaystyle{ Z }[/math]:

[math]\displaystyle{ 0.50=\underset{k=j}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} N \\ k \\ \end{matrix} \right){{Z}^{k}}{{\left( 1-Z \right)}^{N-k}} }[/math]

The same methodology can then be repeated by changing [math]\displaystyle{ P }[/math] for [math]\displaystyle{ 0.50 }[/math] [math]\displaystyle{ (50%) }[/math] to our desired confidence level. For [math]\displaystyle{ P=90% }[/math] one would formulate the equation as

[math]\displaystyle{ 0.90=\underset{k=j}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} N \\ k \\ \end{matrix} \right){{Z}^{k}}{{\left( 1-Z \right)}^{N-k}} }[/math]

Keep in mind that one must be careful to select the appropriate values for [math]\displaystyle{ P }[/math] based on the type of confidence bounds desired. For example, if two-sided 80% confidence bounds are to be calculated, one must solve the equation twice (once with [math]\displaystyle{ P=0.1 }[/math] and once with [math]\displaystyle{ P=0.9 }[/math]) in order to place the bounds around 80% of the population.

Using this methodology, the appropriate ranks are obtained and plotted based on the desired confidence level. These points are then joined by a smooth curve to obtain the corresponding confidence bound.

This non-parametric methodology is only used by Weibull++ when plotting bounds on the mixed Weibull distribution. Full details on this methodology can be found in Kececioglu [20]. These binomial equations can again be transformed using the beta and F distributions, thus the name beta binomial confidence bounds.

Bayesian Confidence Bounds

A fourth method of estimating confidence bounds is based on the Bayes theorem. This type of confidence bounds relies on a different school of thought in statistical analysis, where prior information is combined with sample data in order to make inferences on model parameters and their functions. An introduction to Bayesian methods is given in Chapter 3. Bayesian confidence bounds are derived from Bayes rule, which states that:

[math]\displaystyle{ f(\theta |Data)=\frac{L(Data|\theta )\varphi (\theta )}{\underset{\varsigma }{\int{\mathop{}_{}^{}}}\,L(Data|\theta )\varphi (\theta )d\theta } }[/math]

where:

1. [math]\displaystyle{ f(\theta |Data) }[/math] is the [math]\displaystyle{ posterior }[/math] [math]\displaystyle{ pdf }[/math] of [math]\displaystyle{ \theta }[/math]
2. [math]\displaystyle{ \theta }[/math] is the parameter vector of the chosen distribution (i.e. Weibull, lognormal, etc.)
3. [math]\displaystyle{ L(\bullet ) }[/math] is the likelihood function
4. [math]\displaystyle{ \varphi (\theta ) }[/math] is the [math]\displaystyle{ prior }[/math] [math]\displaystyle{ pdf }[/math] of the parameter vector [math]\displaystyle{ \theta }[/math]
5. [math]\displaystyle{ \varsigma }[/math] is the range of [math]\displaystyle{ \theta }[/math].

In other words, the prior knowledge is provided in the form of the prior [math]\displaystyle{ pdf }[/math] of the parameters, which in turn is combined with the sample data in order to obtain the posterior [math]\displaystyle{ pdf. }[/math] Different forms of prior information exist, such as past data, expert opinion or non-informative (refer to Chapter 3). It can be seen from Eqn. (BayesRule) that we are now dealing with distributions of parameters rather than single value parameters. For example, consider a one-parameter distribution with a positive parameter [math]\displaystyle{ {{\theta }_{1}} }[/math]. Given a set of sample data, and a prior distribution for [math]\displaystyle{ {{\theta }_{1}}, }[/math] [math]\displaystyle{ \varphi ({{\theta }_{1}}), }[/math] Eqn. (BayesRule) can be written as:

[math]\displaystyle{ f({{\theta }_{1}}|Data)=\frac{L(Data|{{\theta }_{1}})\varphi ({{\theta }_{1}})}{\int_{0}^{\infty }L(Data|{{\theta }_{1}})\varphi ({{\theta }_{1}})d{{\theta }_{1}}} }[/math]

In other words, we now have the distribution of [math]\displaystyle{ {{\theta }_{1}} }[/math] and we can now make statistical inferences on this parameter, such as calculating probabilities. Specifically, the probability that [math]\displaystyle{ {{\theta }_{1}} }[/math] is less than or equal to a value [math]\displaystyle{ x, }[/math] [math]\displaystyle{ P({{\theta }_{1}}\le x) }[/math] can be obtained by integrating Eqn. (BayesEX), or:

[math]\displaystyle{ P({{\theta }_{1}}\le x)=\int_{0}^{x}f({{\theta }_{1}}|Data)d{{\theta }_{1}} }[/math]

Eqn. (IntBayes) essentially calculates a confidence bound on the parameter, where [math]\displaystyle{ P({{\theta }_{1}}\le x) }[/math] is the confidence level and [math]\displaystyle{ x }[/math] is the confidence bound. Substituting Eqn. (BayesEX) into Eqn. (IntBayes) yields:

[math]\displaystyle{ CL=\frac{\int_{0}^{x}L(Data|{{\theta }_{1}})\varphi ({{\theta }_{1}})d{{\theta }_{1}}}{\int_{0}^{\infty }L(Data|{{\theta }_{1}})\varphi ({{\theta }_{1}})d{{\theta }_{1}}} }[/math]

The only question at this point is what do we use as a prior distribution of [math]\displaystyle{ {{\theta }_{1}}. }[/math]. For the confidence bounds calculation application, non-informative prior distributions are utilized. Non-informative prior distributions are distributions that have no population basis and play a minimal role in the posterior distribution. The idea behind the use of non-informative prior distributions is to make inferences that are not affected by external information, or when external information is not available. In the general case of calculating confidence bounds using Bayesian methods, the method should be independent of external information and it should only rely on the current data. Therefore, non-informative priors are used. Specifically, the uniform distribution is used as a prior distribution for the different parameters of the selected fitted distribution. For example, if the Weibull distribution is fitted to the data, the prior distributions for beta and eta are assumed to be uniform. Eqn. (BayesCLEX) can be generalized for any distribution having a vector of parameters [math]\displaystyle{ \theta , }[/math] yielding the general equation for calculating Bayesian confidence bounds:

[math]\displaystyle{ CL=\frac{\underset{\xi }{\int{\mathop{}_{}^{}}}\,L(Data|\theta )\varphi (\theta )d\theta }{\underset{\varsigma }{\int{\mathop{}_{}^{}}}\,L(Data|\theta )\varphi (\theta )d\theta } }[/math]

where:

1. [math]\displaystyle{ CL }[/math] is confidence level
2. [math]\displaystyle{ \theta }[/math] is the parameter vector
3. [math]\displaystyle{ L(\bullet ) }[/math] is the likelihood function
4. [math]\displaystyle{ \varphi (\theta ) }[/math] is the prior [math]\displaystyle{ pdf }[/math] of the parameter vector [math]\displaystyle{ \theta }[/math]
5. [math]\displaystyle{ \varsigma }[/math] is the range of [math]\displaystyle{ \theta }[/math]
6. [math]\displaystyle{ \xi }[/math] is the range in which [math]\displaystyle{ \theta }[/math] changes from [math]\displaystyle{ \Psi (T,R) }[/math] till [math]\displaystyle{ {\theta }'s }[/math] maximum value or from [math]\displaystyle{ {\theta }'s }[/math] minimum value till [math]\displaystyle{ \Psi (T,R) }[/math]
7. [math]\displaystyle{ \Psi (T,R) }[/math] is function such that if [math]\displaystyle{ T }[/math] is given then the bounds are calculated for [math]\displaystyle{ R }[/math] and if [math]\displaystyle{ R }[/math] is given, then he bounds are calculated for [math]\displaystyle{ T }[/math].

If [math]\displaystyle{ T }[/math] is given, then from Eqn. (BayesCL) and [math]\displaystyle{ \Psi }[/math] and for a given [math]\displaystyle{ CL, }[/math] the bounds on [math]\displaystyle{ R }[/math] are calculated. If [math]\displaystyle{ R }[/math] is given, then from Eqn. (BayesCL) and [math]\displaystyle{ \Psi }[/math] and for a given [math]\displaystyle{ CL, }[/math] the bounds on [math]\displaystyle{ T }[/math] are calculated.

Confidence Bounds on Time (Type 1)

For a given failure time distribution and a given reliability [math]\displaystyle{ R }[/math], [math]\displaystyle{ T(R) }[/math] is a function of [math]\displaystyle{ R }[/math] and the distribution parameters. To illustrate the procedure for obtaining confidence bounds, the two-parameter Weibull distribution is used as an example. Bounds, for the case of other distributions, can be obtained in similar fashion. For the two-parameter Weibull distribution:

[math]\displaystyle{ T(R)=\eta \exp (\frac{\ln (-\ln R)}{\beta }) }[/math]

For a given reliability, the Bayesian one-sided upper bound estimate for [math]\displaystyle{ T(R) }[/math] is:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,(T\le {{T}_{U}})=\int_{0}^{{{T}_{U}}(R)}f(T|Data,R)dT }[/math]

where [math]\displaystyle{ f(T|Data,R) }[/math] is the posterior distribution of Time [math]\displaystyle{ T. }[/math] Using Eqn. (T bayes), we have the following:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,(T\le {{T}_{U}})=\underset{}{\overset{}{\mathop{\Pr }}}\,(\eta \exp (\frac{\ln (-\ln R)}{\beta })\le {{T}_{U}}) }[/math]

Eqn. (cl) can be rewritten in terms of [math]\displaystyle{ \eta }[/math] as:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,(\eta \le {{T}_{U}}\exp (-\frac{\ln (-\ln R)}{\beta })) }[/math]

From Eqns. (IntBayes), (BayesCLEX) and (BayesCL), by assuming the priors of [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \eta }[/math] are independent, we then obtain the following relationship:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{0}^{{{T}_{U}}\exp (-\frac{\ln (-\ln R)}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math]

Eqn. (cl2) can be solved for [math]\displaystyle{ {{T}_{U}}(R) }[/math], where:

1. [math]\displaystyle{ CL }[/math] is confidence level,
2. [math]\displaystyle{ \varphi (\beta ) }[/math] is the prior [math]\displaystyle{ pdf }[/math] of the parameter [math]\displaystyle{ \beta }[/math]. For non-informative prior distribution, [math]\displaystyle{ \varphi (\beta )=\tfrac{1}{\beta }. }[/math]
3. [math]\displaystyle{ \varphi (\eta ) }[/math] is the prior [math]\displaystyle{ pdf }[/math] of the parameter [math]\displaystyle{ \eta . }[/math]. For non-informative prior distribution, [math]\displaystyle{ \varphi (\eta )=\tfrac{1}{\eta }. }[/math]
4. [math]\displaystyle{ L(\bullet ) }[/math] is the likelihood function.

The same method can be used to get the one-sided lower bound of [math]\displaystyle{ T(R) }[/math] from:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{{{T}_{L}}\exp (\frac{-\ln (-\ln R)}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math]

Eqn. (cl5) can be solved to get [math]\displaystyle{ {{T}_{L}}(R) }[/math].
The Bayesian two-sided bounds estimate for [math]\displaystyle{ T(R) }[/math] is:

[math]\displaystyle{ CL=\int_{{{T}_{L}}(R)}^{{{T}_{U}}(R)}f(T|Data,R)dT }[/math]

which is equivalent to:

[math]\displaystyle{ (1+CL)/2=\int_{0}^{{{T}_{U}}(R)}f(T|Data,R)dT }[/math]

and:

[math]\displaystyle{ (1-CL)/2=\int_{0}^{{{T}_{L}}(R)}f(T|Data,R)dT }[/math]

Using the same method for the one-sided bounds, [math]\displaystyle{ {{T}_{U}}(R) }[/math] and [math]\displaystyle{ {{T}_{L}}(R) }[/math] can be solved.

Confidence Bounds on Reliability (Type 2)

For a given failure time distribution and a given time [math]\displaystyle{ T }[/math], [math]\displaystyle{ R(T) }[/math] is a function of [math]\displaystyle{ T }[/math] and the distribution parameters. To illustrate the procedure for obtaining confidence bounds, the two-parameter Weibull distribution is used as an example. Bounds, for the case of other distributions, can be obtained in similar fashion. For example, for two parameter Weibull distribution:

[math]\displaystyle{ R=\exp (-{{(\frac{T}{\eta })}^{\beta }}) }[/math]

The Bayesian one-sided upper bound estimate for [math]\displaystyle{ R(T) }[/math] is:

[math]\displaystyle{ CL=\int_{0}^{{{R}_{U}}(T)}f(R|Data,T)dR }[/math]

Similar with the bounds on Time, the following is obtained:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{0}^{T\exp (-\frac{\ln (-\ln {{R}_{U}})}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math]

Eqn. (cl3) can be solved to get [math]\displaystyle{ {{R}_{U}}(T) }[/math].

The Bayesian one-sided lower bound estimate for R(T) is:

[math]\displaystyle{ 1-CL=\int_{0}^{{{R}_{L}}(T)}f(R|Data,T)dR }[/math]

Using the posterior distribution, the following is obtained:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{T\exp (-\frac{\ln (-\ln {{R}_{L}})}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math]

Eqn. (cl4) can be solved to get [math]\displaystyle{ {{R}_{L}}(T) }[/math].
The Bayesian two-sided bounds estimate for [math]\displaystyle{ R(T) }[/math] is:

[math]\displaystyle{ CL=\int_{{{R}_{L}}(T)}^{{{R}_{U}}(T)}f(R|Data,T)dR }[/math]

which is equivalent to:

[math]\displaystyle{ \int_{0}^{{{R}_{U}}(T)}f(R|Data,T)dR=(1+CL)/2 }[/math]

and

[math]\displaystyle{ \int_{0}^{{{R}_{L}}(T)}f(R|Data,T)dR=(1-CL)/2 }[/math]

Using the same method for one-sided bounds, [math]\displaystyle{ {{R}_{U}}(T) }[/math] and [math]\displaystyle{ {{R}_{L}}(T) }[/math] can be solved.

Simulation Based Bounds

The SimuMatic tool in Weibull++ can be used to perform a large number of reliability analyses on data sets that have been created using Monte Carlo simulation. This utility can assist the analyst to a) better understand life data analysis concepts, b) experiment with the influences of sample sizes and censoring schemes on analysis methods, c) construct simulation-based confidence intervals, d) better understand the concepts behind confidence intervals and e) design reliability tests. This section describes how to use simulation for estimating confidence bounds.
SimuMatic generates confidence bounds and assists in visualizing and understanding them. In addition, it allows one to determine the adequacy of certain parameter estimation methods (such as rank regression on X, rank regression on Y and maximum likelihood estimation) and to visualize the effects of different data censoring schemes on the confidence bounds.

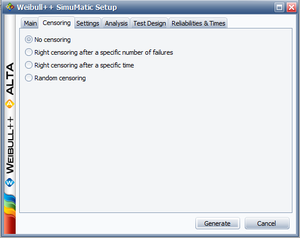
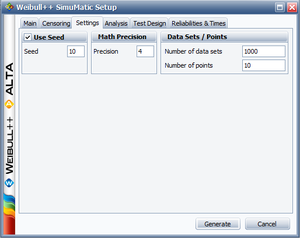
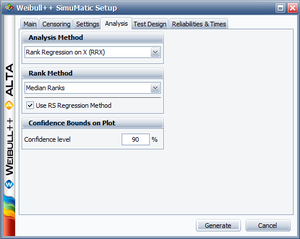
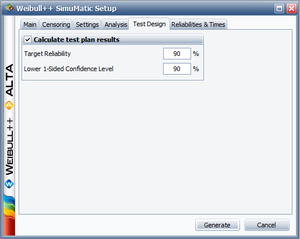
Example 4

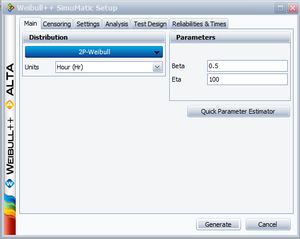
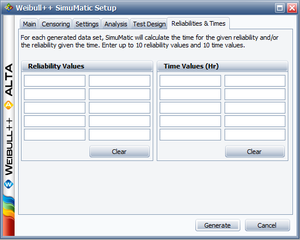
The purpose of this example is to determine the best parameter estimation method for a sample of ten units following a Weibull distribution with [math]\displaystyle{ \beta =2 }[/math] and [math]\displaystyle{ \eta =100 }[/math] and with complete time-to-failure data for each unit (i.e. no censoring). The number of generated data sets is set to 10,000. The SimuMatic inputs are shown next.

The parameters are estimated using RRX, RRY and MLE. The plotted results generated by SimuMatic are shown next.

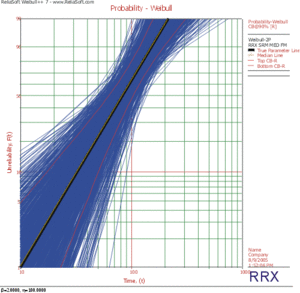
Using RRX:

Using RRY:

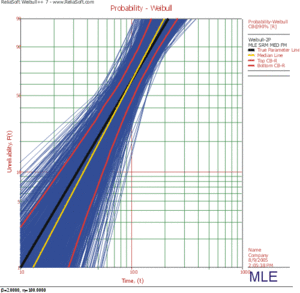
Using MLE:

The results clearly demonstrate that the median RRX estimate provides the least deviation from the truth for this sample size and data type. However, the MLE outputs are grouped more closely together, as evidenced by the bounds. The previous figures also show the simulation-based bounds, as well as the expected variation due to sampling error.

This experiment can be repeated in SimuMatic using multiple censoring schemes (including Type I and Type II right censoring as well as random censoring) with various distributions. Multiple experiments can be performed with this utility to evaluate assumptions about the appropriate parameter estimation method to use for data sets.

Fisher Matrix Confidence Bounds

This section presents an overview of the theory on obtaining approximate confidence bounds on suspended (multiply censored) data. The methodology used is the so-called Fisher matrix bounds (FM), described in [[Nelson [30]]] and [[Lloyd and Lipow [24]]]. These bounds are employed in most other commercial statistical applications. In general, these bounds tend to be more optimistic than the non-parametric rank based bounds. This may be a concern, particularly when dealing with small sample sizes. Some statisticians feel that the Fisher matrix bounds are too optimistic when dealing with small sample sizes and prefer to use other techniques for calculating confidence bounds, such as the likelihood ratio bounds.

Approximate Estimates of the Mean and Variance of a Function

In utilizing FM bounds for functions, one must first determine the mean and variance of the function in question (i.e. reliability function, failure rate function, etc.). An example of the methodology and assumptions for an arbitrary function [math]\displaystyle{ G }[/math] is presented next.

Single Parameter Case

For simplicity, consider a one-parameter distribution represented by a general function, [math]\displaystyle{ G, }[/math] which is a function of one parameter estimator, say [math]\displaystyle{ G(\widehat{\theta }). }[/math] For example, the mean of the exponential distribution is a function of the parameter [math]\displaystyle{ \lambda }[/math]: [math]\displaystyle{ G(\lambda )=1/\lambda =\mu }[/math]. Then, in general, the expected value of [math]\displaystyle{ G\left( \widehat{\theta } \right) }[/math] can be found by:

[math]\displaystyle{ E\left( G\left( \widehat{\theta } \right) \right)=G(\theta )+O\left( \frac{1}{n} \right) }[/math]

where [math]\displaystyle{ G(\theta ) }[/math] is some function of [math]\displaystyle{ \theta }[/math], such as the reliability function, and [math]\displaystyle{ \theta }[/math] is the population parameter where [math]\displaystyle{ E\left( \widehat{\theta } \right)=\theta }[/math] as [math]\displaystyle{ n\to \infty }[/math] . The term [math]\displaystyle{ O\left( \tfrac{1}{n} \right) }[/math] is a function of [math]\displaystyle{ n }[/math], the sample size, and tends to zero, as fast as [math]\displaystyle{ \tfrac{1}{n}, }[/math] as [math]\displaystyle{ n\to \infty . }[/math] For example, in the case of [math]\displaystyle{ \widehat{\theta }=1/\overline{x} }[/math] and [math]\displaystyle{ G(x)=1/x }[/math], then [math]\displaystyle{ E(G(\widehat{\theta }))=\overline{x}+O\left( \tfrac{1}{n} \right) }[/math] where [math]\displaystyle{ O\left( \tfrac{1}{n} \right)=\tfrac{{{\sigma }^{2}}}{n} }[/math]. Thus as [math]\displaystyle{ n\to \infty }[/math], [math]\displaystyle{ E(G(\widehat{\theta }))=\mu }[/math] where [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \sigma }[/math] are the mean and standard deviation, respectively. Using the same one-parameter distribution, the variance of the function [math]\displaystyle{ G\left( \widehat{\theta } \right) }[/math] can then be estimated by:

[math]\displaystyle{ Var\left( G\left( \widehat{\theta } \right) \right)=\left( \frac{\partial G}{\partial \widehat{\theta }} \right)_{\widehat{\theta }=\theta }^{2}Var\left( \widehat{\theta } \right)+O\left( \frac{1}{{{n}^{\tfrac{3}{2}}}} \right) }[/math]

Two-Parameter Case

Consider a Weibull distribution with two parameters [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \eta }[/math]. For a given value of [math]\displaystyle{ T }[/math], [math]\displaystyle{ R(T)=G(\beta ,\eta )={{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}} }[/math]. Repeating the previous method for the case of a two-parameter distribution, it is generally true that for a function [math]\displaystyle{ G }[/math], which is a function of two parameter estimators, say [math]\displaystyle{ G\left( {{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}} \right) }[/math], that:

[math]\displaystyle{ E\left( G\left( {{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}} \right) \right)=G\left( {{\theta }_{1}},{{\theta }_{2}} \right)+O\left( \frac{1}{n} \right) }[/math]

and:

[math]\displaystyle{ \begin{align} Var( G( {{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}}))= &{(\frac{\partial G}{\partial {{\widehat{\theta }}_{1}}})^2}_{{\widehat{\theta_{1}}}={\theta_{1}}}Var(\widehat{\theta_{1}})+{(\frac{\partial G}{\partial {{\widehat{\theta }}_{2}}})^2}_{{\widehat{\theta_{2}}}={\theta_{1}}}Var(\widehat{\theta_{2}})\\ & +2{(\frac{\partial G}{\partial {{\widehat{\theta }}_{1}}})^2}_{{\widehat{\theta_{1}}}={\theta_{1}}}{(\frac{\partial G}{\partial {{\widehat{\theta }}_{2}}})^2}_{{\widehat{\theta_{2}}}={\theta_{1}}}Cov(\widehat{\theta_{1}},\widehat{\theta_{2}}) \\ & +O(\frac{1}{n^{\tfrac{3}{2}}}) \end{align} }[/math]

Note that the derivatives of Eqn. (var) are evaluated at [math]\displaystyle{ {{\widehat{\theta }}_{1}}={{\theta }_{1}} }[/math] and [math]\displaystyle{ {{\widehat{\theta }}_{2}}={{\theta }_{1}}, }[/math] where E [math]\displaystyle{ \left( {{\widehat{\theta }}_{1}} \right)\simeq {{\theta }_{1}} }[/math] and E [math]\displaystyle{ \left( {{\widehat{\theta }}_{2}} \right)\simeq {{\theta }_{2}}. }[/math]

Parameter Variance and Covariance Determination

The determination of the variance and covariance of the parameters is accomplished via the use of the Fisher information matrix. For a two-parameter distribution, and using maximum likelihood estimates (MLE), the log-likelihood function for censored data is given by:

[math]\displaystyle{ \begin{align} \ln [L]= & \Lambda =\underset{i=1}{\overset{R}{\mathop \sum }}\,\ln [f({{T}_{i}};{{\theta }_{1}},{{\theta }_{2}})] \\ & \text{ }+\underset{j=1}{\overset{M}{\mathop \sum }}\,\ln [1-F({{S}_{j}};{{\theta }_{1}},{{\theta }_{2}})] \\ & \text{ }+\underset{l=1}{\overset{P}{\mathop \sum }}\,\ln \left\{ F({{I}_{{{l}_{U}}}};{{\theta }_{1}},{{\theta }_{2}})-F({{I}_{{{l}_{L}}}};{{\theta }_{1}},{{\theta }_{2}}) \right\} \end{align} }[/math]

In the equation above, the first summation is for complete data, the second summation is for right censored data, and the third summation is for interval or left censored data. For more information on these data types, see Chapter 4.
Then the Fisher information matrix is given by:

[math]\displaystyle{ {{F}_{0}}=\left[ \begin{matrix} {{E}_{0}}{{\left[ -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{1}^{2}} \right]}_{0}} & {} & {{E}_{0}}{{\left[ -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{1}}\partial {{\theta }_{2}}} \right]}_{0}} \\ {} & {} & {} \\ {{E}_{0}}{{\left[ -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{2}}\partial {{\theta }_{1}}} \right]}_{0}} & {} & {{E}_{0}}{{\left[ -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{2}^{2}} \right]}_{0}} \\ \end{matrix} \right] }[/math]

The subscript [math]\displaystyle{ 0 }[/math] indicates that the quantity is evaluated at [math]\displaystyle{ {{\theta }_{1}}={{\theta }_{{{1}_{0}}}} }[/math] and [math]\displaystyle{ {{\theta }_{2}}={{\theta }_{{{2}_{0}}}}, }[/math] the true values of the parameters.
So for a sample of [math]\displaystyle{ N }[/math] units where [math]\displaystyle{ R }[/math] units have failed, [math]\displaystyle{ S }[/math] have been suspended, and [math]\displaystyle{ P }[/math] have failed within a time interval, and [math]\displaystyle{ N=R+M+P, }[/math] one could obtain the sample local information matrix by:

[math]\displaystyle{ F={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{1}^{2}} & {} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{1}}\partial {{\theta }_{2}}} \\ {} & {} & {} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{2}}\partial {{\theta }_{1}}} & {} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{2}^{2}} \\ \end{matrix} \right]}^{}} }[/math]

Substituting in the values of the estimated parameters, in this case [math]\displaystyle{ {{\widehat{\theta }}_{1}} }[/math] and [math]\displaystyle{ {{\widehat{\theta }}_{2}} }[/math], and then inverting the matrix, one can then obtain the local estimate of the covariance matrix or:

[math]\displaystyle{ \left[ \begin{matrix} \widehat{Var}\left( {{\widehat{\theta }}_{1}} \right) & {} & \widehat{Cov}\left( {{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}} \right) \\ {} & {} & {} \\ \widehat{Cov}\left( {{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}} \right) & {} & \widehat{Var}\left( {{\widehat{\theta }}_{2}} \right) \\ \end{matrix} \right]={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{1}^{2}} & {} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{1}}\partial {{\theta }_{2}}} \\ {} & {} & {} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\theta }_{2}}\partial {{\theta }_{1}}} & {} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \theta _{2}^{2}} \\ \end{matrix} \right]}^{-1}} }[/math]

Then the variance of a function ([math]\displaystyle{ Var(G) }[/math]) can be estimated using Eqn. (var). Values for the variance and covariance of the parameters are obtained from Eqn. (Fisher2). Once they have been obtained, the approximate confidence bounds on the function are given as:

[math]\displaystyle{ C{{B}_{R}}=E(G)\pm {{z}_{\alpha }}\sqrt{Var(G)} }[/math]

which is the estimated value plus or minus a certain number of standard deviations. We address finding [math]\displaystyle{ {{z}_{\alpha }} }[/math] next.

Approximate Confidence Intervals on the Parameters

In general, MLE estimates of the parameters are asymptotically normal, meaning for large sample sizes that a distribution of parameter estimates from the same population would be very close to the normal distribution. Thus if [math]\displaystyle{ \widehat{\theta } }[/math] is the MLE estimator for [math]\displaystyle{ \theta }[/math], in the case of a single parameter distribution, estimated from a large sample of [math]\displaystyle{ n }[/math] units and if:

[math]\displaystyle{ z\equiv \frac{\widehat{\theta }-\theta }{\sqrt{Var\left( \widehat{\theta } \right)}} }[/math]

then using the normal distribution of [math]\displaystyle{ z\ \ : }[/math]

[math]\displaystyle{ P\left( x\le z \right)\to \Phi \left( z \right)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{z}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt }[/math]

for large [math]\displaystyle{ n }[/math]. We now place confidence bounds on [math]\displaystyle{ \theta , }[/math] at some confidence level [math]\displaystyle{ \delta }[/math], bounded by the two end points [math]\displaystyle{ {{C}_{1}} }[/math] and [math]\displaystyle{ {{C}_{2}} }[/math] where:

[math]\displaystyle{ P\left( {{C}_{1}}\lt \theta \lt {{C}_{2}} \right)=\delta }[/math]

From Eqn. (e729):

[math]\displaystyle{ P\left( -{{K}_{\tfrac{1-\delta }{2}}}\lt \frac{\widehat{\theta }-\theta }{\sqrt{Var\left( \widehat{\theta } \right)}}\lt {{K}_{\tfrac{1-\delta }{2}}} \right)\simeq \delta }[/math]

where [math]\displaystyle{ {{K}_{\alpha }} }[/math] is defined by:

[math]\displaystyle{ \alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi \left( {{K}_{\alpha }} \right) }[/math]

Now by simplifying Eqn. (e731), one can obtain the approximate two-sided confidence bounds on the parameter [math]\displaystyle{ \theta , }[/math] at a confidence level [math]\displaystyle{ \delta , }[/math] or:

[math]\displaystyle{ \left( \widehat{\theta }-{{K}_{\tfrac{1-\delta }{2}}}\cdot \sqrt{Var\left( \widehat{\theta } \right)}\lt \theta \lt \widehat{\theta }+{{K}_{\tfrac{1-\delta }{2}}}\cdot \sqrt{Var\left( \widehat{\theta } \right)} \right) }[/math]

The upper one-sided bounds are given by:

[math]\displaystyle{ \theta \lt \widehat{\theta }+{{K}_{1-\delta }}\sqrt{Var(\widehat{\theta })} }[/math]

while the lower one-sided bounds are given by:

[math]\displaystyle{ \theta \gt \widehat{\theta }-{{K}_{1-\delta }}\sqrt{Var(\widehat{\theta })} }[/math]

If [math]\displaystyle{ \widehat{\theta } }[/math] must be positive, then [math]\displaystyle{ \ln \widehat{\theta } }[/math] is treated as normally distributed. The two-sided approximate confidence bounds on the parameter [math]\displaystyle{ \theta }[/math], at confidence level [math]\displaystyle{ \delta }[/math], then become:

[math]\displaystyle{ \begin{align} & {{\theta }_{U}}= & \widehat{\theta }\cdot {{e}^{\tfrac{{{K}_{\tfrac{1-\delta }{2}}}\sqrt{Var\left( \widehat{\theta } \right)}}{\widehat{\theta }}}}\text{ (Two-sided upper)} \\ & {{\theta }_{L}}= & \frac{\widehat{\theta }}{{{e}^{\tfrac{{{K}_{\tfrac{1-\delta }{2}}}\sqrt{Var\left( \widehat{\theta } \right)}}{\widehat{\theta }}}}}\text{ (Two-sided lower)} \end{align} }[/math]

The one-sided approximate confidence bounds on the parameter [math]\displaystyle{ \theta }[/math], at confidence level [math]\displaystyle{ \delta , }[/math] can be found from:

[math]\displaystyle{ \begin{align} & {{\theta }_{U}}= & \widehat{\theta }\cdot {{e}^{\tfrac{{{K}_{1-\delta }}\sqrt{Var\left( \widehat{\theta } \right)}}{\widehat{\theta }}}}\text{ (One-sided upper)} \\ & {{\theta }_{L}}= & \frac{\widehat{\theta }}{{{e}^{\tfrac{{{K}_{1-\delta }}\sqrt{Var\left( \widehat{\theta } \right)}}{\widehat{\theta }}}}}\text{ (One-sided lower)} \end{align} }[/math]

The same procedure can be extended for the case of a two or more parameter distribution. Lloyd and Lipow [24] further elaborate on this procedure.

Confidence Bounds on Time (Type 1)

Type 1 confidence bounds are confidence bounds around time for a given reliability. For example, when using the one-parameter exponential distribution, the corresponding time for a given exponential percentile (i.e. y-ordinate or unreliability, [math]\displaystyle{ Q=1-R) }[/math] is determined by solving the unreliability function for the time, [math]\displaystyle{ T }[/math], or:

[math]\displaystyle{ \begin{align}\widehat{T}(Q)= &-\frac{1}{\widehat{\lambda }} \ln (1-Q)= & -\frac{1}{\widehat{\lambda }}\ln (R) \end{align} }[/math]

Bounds on time (Type 1) return the confidence bounds around this time value by determining the confidence intervals around [math]\displaystyle{ \widehat{\lambda } }[/math] and substituting these values into Eqn. (cb). The bounds on [math]\displaystyle{ \widehat{\lambda } }[/math] were determined using Eqns. (cblmu) and (cblml), with its variance obtained from Eqn. (Fisher2). Note that the procedure is slightly more complicated for distributions with more than one parameter.

Confidence Bounds on Reliability (Type 2)

Type 2 confidence bounds are confidence bounds around reliability. For example, when using the two-parameter exponential distribution, the reliability function is:

[math]\displaystyle{ \widehat{R}(T)={{e}^{-\widehat{\lambda }\cdot T}} }[/math]

Reliability bounds (Type 2) return the confidence bounds by determining the confidence intervals around [math]\displaystyle{ \widehat{\lambda } }[/math] and substituting these values into Eqn. (cbr). The bounds on [math]\displaystyle{ \widehat{\lambda } }[/math] were determined using Eqns. (cblmu) and (cblml), with its variance obtained from Eqn. (Fisher2). Once again, the procedure is more complicated for distributions with more than one parameter.

Beta Binomial Confidence Bounds

Another less mathematically intensive method of calculating confidence bounds involves a procedure similar to that used in calculating median ranks (see Chapter 4). This is a non-parametric approach to confidence interval calculations that involves the use of rank tables and is commonly known as beta-binomial bounds (BB). By non-parametric, we mean that no underlying distribution is assumed. (Parametric implies that an underlying distribution, with parameters, is assumed.) In other words, this method can be used for any distribution, without having to make adjustments in the underlying equations based on the assumed distribution. Recall from the discussion on the median ranks that we used the binomial equation to compute the ranks at the 50% confidence level (or median ranks) by solving the cumulative binomial distribution for [math]\displaystyle{ Z }[/math] (rank for the [math]\displaystyle{ {{j}^{th}} }[/math] failure):

[math]\displaystyle{ P=\underset{k=j}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} N \\ k \\ \end{matrix} \right){{Z}^{k}}{{\left( 1-Z \right)}^{N-k}} }[/math]

where [math]\displaystyle{ N }[/math] is the sample size and [math]\displaystyle{ j }[/math] is the order number.
The median rank was obtained by solving the following equation for [math]\displaystyle{ Z }[/math]:

[math]\displaystyle{ 0.50=\underset{k=j}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} N \\ k \\ \end{matrix} \right){{Z}^{k}}{{\left( 1-Z \right)}^{N-k}} }[/math]

The same methodology can then be repeated by changing [math]\displaystyle{ P }[/math] for [math]\displaystyle{ 0.50 }[/math] [math]\displaystyle{ (50%) }[/math] to our desired confidence level. For [math]\displaystyle{ P=90% }[/math] one would formulate the equation as

[math]\displaystyle{ 0.90=\underset{k=j}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} N \\ k \\ \end{matrix} \right){{Z}^{k}}{{\left( 1-Z \right)}^{N-k}} }[/math]

Keep in mind that one must be careful to select the appropriate values for [math]\displaystyle{ P }[/math] based on the type of confidence bounds desired. For example, if two-sided 80% confidence bounds are to be calculated, one must solve the equation twice (once with [math]\displaystyle{ P=0.1 }[/math] and once with [math]\displaystyle{ P=0.9 }[/math]) in order to place the bounds around 80% of the population.

Using this methodology, the appropriate ranks are obtained and plotted based on the desired confidence level. These points are then joined by a smooth curve to obtain the corresponding confidence bound.

This non-parametric methodology is only used by Weibull++ when plotting bounds on the mixed Weibull distribution. Full details on this methodology can be found in Kececioglu [20]. These binomial equations can again be transformed using the beta and F distributions, thus the name beta binomial confidence bounds.

Bayesian Confidence Bounds

A fourth method of estimating confidence bounds is based on the Bayes theorem. This type of confidence bounds relies on a different school of thought in statistical analysis, where prior information is combined with sample data in order to make inferences on model parameters and their functions. An introduction to Bayesian methods is given in Chapter 3. Bayesian confidence bounds are derived from Bayes rule, which states that:

[math]\displaystyle{ f(\theta |Data)=\frac{L(Data|\theta )\varphi (\theta )}{\underset{\varsigma }{\int{\mathop{}_{}^{}}}\,L(Data|\theta )\varphi (\theta )d\theta } }[/math]

where:

1. [math]\displaystyle{ f(\theta |Data) }[/math] is the [math]\displaystyle{ posterior }[/math] [math]\displaystyle{ pdf }[/math] of [math]\displaystyle{ \theta }[/math]
2. [math]\displaystyle{ \theta }[/math] is the parameter vector of the chosen distribution (i.e. Weibull, lognormal, etc.)
3. [math]\displaystyle{ L(\bullet ) }[/math] is the likelihood function
4. [math]\displaystyle{ \varphi (\theta ) }[/math] is the [math]\displaystyle{ prior }[/math] [math]\displaystyle{ pdf }[/math] of the parameter vector [math]\displaystyle{ \theta }[/math]
5. [math]\displaystyle{ \varsigma }[/math] is the range of [math]\displaystyle{ \theta }[/math].

In other words, the prior knowledge is provided in the form of the prior [math]\displaystyle{ pdf }[/math] of the parameters, which in turn is combined with the sample data in order to obtain the posterior [math]\displaystyle{ pdf. }[/math] Different forms of prior information exist, such as past data, expert opinion or non-informative (refer to Chapter 3). It can be seen from Eqn. (BayesRule) that we are now dealing with distributions of parameters rather than single value parameters. For example, consider a one-parameter distribution with a positive parameter [math]\displaystyle{ {{\theta }_{1}} }[/math]. Given a set of sample data, and a prior distribution for [math]\displaystyle{ {{\theta }_{1}}, }[/math] [math]\displaystyle{ \varphi ({{\theta }_{1}}), }[/math] Eqn. (BayesRule) can be written as:

[math]\displaystyle{ f({{\theta }_{1}}|Data)=\frac{L(Data|{{\theta }_{1}})\varphi ({{\theta }_{1}})}{\int_{0}^{\infty }L(Data|{{\theta }_{1}})\varphi ({{\theta }_{1}})d{{\theta }_{1}}} }[/math]

In other words, we now have the distribution of [math]\displaystyle{ {{\theta }_{1}} }[/math] and we can now make statistical inferences on this parameter, such as calculating probabilities. Specifically, the probability that [math]\displaystyle{ {{\theta }_{1}} }[/math] is less than or equal to a value [math]\displaystyle{ x, }[/math] [math]\displaystyle{ P({{\theta }_{1}}\le x) }[/math] can be obtained by integrating Eqn. (BayesEX), or:

[math]\displaystyle{ P({{\theta }_{1}}\le x)=\int_{0}^{x}f({{\theta }_{1}}|Data)d{{\theta }_{1}} }[/math]

Eqn. (IntBayes) essentially calculates a confidence bound on the parameter, where [math]\displaystyle{ P({{\theta }_{1}}\le x) }[/math] is the confidence level and [math]\displaystyle{ x }[/math] is the confidence bound. Substituting Eqn. (BayesEX) into Eqn. (IntBayes) yields:

[math]\displaystyle{ CL=\frac{\int_{0}^{x}L(Data|{{\theta }_{1}})\varphi ({{\theta }_{1}})d{{\theta }_{1}}}{\int_{0}^{\infty }L(Data|{{\theta }_{1}})\varphi ({{\theta }_{1}})d{{\theta }_{1}}} }[/math]

The only question at this point is what do we use as a prior distribution of [math]\displaystyle{ {{\theta }_{1}}. }[/math]. For the confidence bounds calculation application, non-informative prior distributions are utilized. Non-informative prior distributions are distributions that have no population basis and play a minimal role in the posterior distribution. The idea behind the use of non-informative prior distributions is to make inferences that are not affected by external information, or when external information is not available. In the general case of calculating confidence bounds using Bayesian methods, the method should be independent of external information and it should only rely on the current data. Therefore, non-informative priors are used. Specifically, the uniform distribution is used as a prior distribution for the different parameters of the selected fitted distribution. For example, if the Weibull distribution is fitted to the data, the prior distributions for beta and eta are assumed to be uniform. Eqn. (BayesCLEX) can be generalized for any distribution having a vector of parameters [math]\displaystyle{ \theta , }[/math] yielding the general equation for calculating Bayesian confidence bounds:

[math]\displaystyle{ CL=\frac{\underset{\xi }{\int{\mathop{}_{}^{}}}\,L(Data|\theta )\varphi (\theta )d\theta }{\underset{\varsigma }{\int{\mathop{}_{}^{}}}\,L(Data|\theta )\varphi (\theta )d\theta } }[/math]

where:

1. [math]\displaystyle{ CL }[/math] is confidence level
2. [math]\displaystyle{ \theta }[/math] is the parameter vector
3. [math]\displaystyle{ L(\bullet ) }[/math] is the likelihood function
4. [math]\displaystyle{ \varphi (\theta ) }[/math] is the prior [math]\displaystyle{ pdf }[/math] of the parameter vector [math]\displaystyle{ \theta }[/math]
5. [math]\displaystyle{ \varsigma }[/math] is the range of [math]\displaystyle{ \theta }[/math]
6. [math]\displaystyle{ \xi }[/math] is the range in which [math]\displaystyle{ \theta }[/math] changes from [math]\displaystyle{ \Psi (T,R) }[/math] till [math]\displaystyle{ {\theta }'s }[/math] maximum value or from [math]\displaystyle{ {\theta }'s }[/math] minimum value till [math]\displaystyle{ \Psi (T,R) }[/math]
7. [math]\displaystyle{ \Psi (T,R) }[/math] is function such that if [math]\displaystyle{ T }[/math] is given then the bounds are calculated for [math]\displaystyle{ R }[/math] and if [math]\displaystyle{ R }[/math] is given, then he bounds are calculated for [math]\displaystyle{ T }[/math].

If [math]\displaystyle{ T }[/math] is given, then from Eqn. (BayesCL) and [math]\displaystyle{ \Psi }[/math] and for a given [math]\displaystyle{ CL, }[/math] the bounds on [math]\displaystyle{ R }[/math] are calculated. If [math]\displaystyle{ R }[/math] is given, then from Eqn. (BayesCL) and [math]\displaystyle{ \Psi }[/math] and for a given [math]\displaystyle{ CL, }[/math] the bounds on [math]\displaystyle{ T }[/math] are calculated.

Confidence Bounds on Time (Type 1)

For a given failure time distribution and a given reliability [math]\displaystyle{ R }[/math], [math]\displaystyle{ T(R) }[/math] is a function of [math]\displaystyle{ R }[/math] and the distribution parameters. To illustrate the procedure for obtaining confidence bounds, the two-parameter Weibull distribution is used as an example. Bounds, for the case of other distributions, can be obtained in similar fashion. For the two-parameter Weibull distribution:

[math]\displaystyle{ T(R)=\eta \exp (\frac{\ln (-\ln R)}{\beta }) }[/math]

For a given reliability, the Bayesian one-sided upper bound estimate for [math]\displaystyle{ T(R) }[/math] is:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,(T\le {{T}_{U}})=\int_{0}^{{{T}_{U}}(R)}f(T|Data,R)dT }[/math]

where [math]\displaystyle{ f(T|Data,R) }[/math] is the posterior distribution of Time [math]\displaystyle{ T. }[/math] Using Eqn. (T bayes), we have the following:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,(T\le {{T}_{U}})=\underset{}{\overset{}{\mathop{\Pr }}}\,(\eta \exp (\frac{\ln (-\ln R)}{\beta })\le {{T}_{U}}) }[/math]

Eqn. (cl) can be rewritten in terms of [math]\displaystyle{ \eta }[/math] as:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,(\eta \le {{T}_{U}}\exp (-\frac{\ln (-\ln R)}{\beta })) }[/math]

From Eqns. (IntBayes), (BayesCLEX) and (BayesCL), by assuming the priors of [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \eta }[/math] are independent, we then obtain the following relationship:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{0}^{{{T}_{U}}\exp (-\frac{\ln (-\ln R)}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math]

Eqn. (cl2) can be solved for [math]\displaystyle{ {{T}_{U}}(R) }[/math], where:

1. [math]\displaystyle{ CL }[/math] is confidence level,
2. [math]\displaystyle{ \varphi (\beta ) }[/math] is the prior [math]\displaystyle{ pdf }[/math] of the parameter [math]\displaystyle{ \beta }[/math]. For non-informative prior distribution, [math]\displaystyle{ \varphi (\beta )=\tfrac{1}{\beta }. }[/math]
3. [math]\displaystyle{ \varphi (\eta ) }[/math] is the prior [math]\displaystyle{ pdf }[/math] of the parameter [math]\displaystyle{ \eta . }[/math]. For non-informative prior distribution, [math]\displaystyle{ \varphi (\eta )=\tfrac{1}{\eta }. }[/math]
4. [math]\displaystyle{ L(\bullet ) }[/math] is the likelihood function.

The same method can be used to get the one-sided lower bound of [math]\displaystyle{ T(R) }[/math] from:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{{{T}_{L}}\exp (\frac{-\ln (-\ln R)}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math]

Eqn. (cl5) can be solved to get [math]\displaystyle{ {{T}_{L}}(R) }[/math].
The Bayesian two-sided bounds estimate for [math]\displaystyle{ T(R) }[/math] is:

[math]\displaystyle{ CL=\int_{{{T}_{L}}(R)}^{{{T}_{U}}(R)}f(T|Data,R)dT }[/math]

which is equivalent to:

[math]\displaystyle{ (1+CL)/2=\int_{0}^{{{T}_{U}}(R)}f(T|Data,R)dT }[/math]

and:

[math]\displaystyle{ (1-CL)/2=\int_{0}^{{{T}_{L}}(R)}f(T|Data,R)dT }[/math]

Using the same method for the one-sided bounds, [math]\displaystyle{ {{T}_{U}}(R) }[/math] and [math]\displaystyle{ {{T}_{L}}(R) }[/math] can be solved.

Confidence Bounds on Reliability (Type 2)

For a given failure time distribution and a given time [math]\displaystyle{ T }[/math], [math]\displaystyle{ R(T) }[/math] is a function of [math]\displaystyle{ T }[/math] and the distribution parameters. To illustrate the procedure for obtaining confidence bounds, the two-parameter Weibull distribution is used as an example. Bounds, for the case of other distributions, can be obtained in similar fashion. For example, for two parameter Weibull distribution:

[math]\displaystyle{ R=\exp (-{{(\frac{T}{\eta })}^{\beta }}) }[/math]

The Bayesian one-sided upper bound estimate for [math]\displaystyle{ R(T) }[/math] is:

[math]\displaystyle{ CL=\int_{0}^{{{R}_{U}}(T)}f(R|Data,T)dR }[/math]

Similar with the bounds on Time, the following is obtained:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{0}^{T\exp (-\frac{\ln (-\ln {{R}_{U}})}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math]

Eqn. (cl3) can be solved to get [math]\displaystyle{ {{R}_{U}}(T) }[/math].

The Bayesian one-sided lower bound estimate for R(T) is:

[math]\displaystyle{ 1-CL=\int_{0}^{{{R}_{L}}(T)}f(R|Data,T)dR }[/math]

Using the posterior distribution, the following is obtained:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{T\exp (-\frac{\ln (-\ln {{R}_{L}})}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math]

Eqn. (cl4) can be solved to get [math]\displaystyle{ {{R}_{L}}(T) }[/math].
The Bayesian two-sided bounds estimate for [math]\displaystyle{ R(T) }[/math] is:

[math]\displaystyle{ CL=\int_{{{R}_{L}}(T)}^{{{R}_{U}}(T)}f(R|Data,T)dR }[/math]

which is equivalent to:

[math]\displaystyle{ \int_{0}^{{{R}_{U}}(T)}f(R|Data,T)dR=(1+CL)/2 }[/math]

and

[math]\displaystyle{ \int_{0}^{{{R}_{L}}(T)}f(R|Data,T)dR=(1-CL)/2 }[/math]

Using the same method for one-sided bounds, [math]\displaystyle{ {{R}_{U}}(T) }[/math] and [math]\displaystyle{ {{R}_{L}}(T) }[/math] can be solved.

Simulation Based Bounds

The SimuMatic tool in Weibull++ can be used to perform a large number of reliability analyses on data sets that have been created using Monte Carlo simulation. This utility can assist the analyst to a) better understand life data analysis concepts, b) experiment with the influences of sample sizes and censoring schemes on analysis methods, c) construct simulation-based confidence intervals, d) better understand the concepts behind confidence intervals and e) design reliability tests. This section describes how to use simulation for estimating confidence bounds.
SimuMatic generates confidence bounds and assists in visualizing and understanding them. In addition, it allows one to determine the adequacy of certain parameter estimation methods (such as rank regression on X, rank regression on Y and maximum likelihood estimation) and to visualize the effects of different data censoring schemes on the confidence bounds.

Example 4

The purpose of this example is to determine the best parameter estimation method for a sample of ten units following a Weibull distribution with [math]\displaystyle{ \beta =2 }[/math] and [math]\displaystyle{ \eta =100 }[/math] and with complete time-to-failure data for each unit (i.e. no censoring). The number of generated data sets is set to 10,000. The SimuMatic inputs are shown next.

The parameters are estimated using RRX, RRY and MLE. The plotted results generated by SimuMatic are shown next.

Using RRX:

Using RRY:

Using MLE:

The results clearly demonstrate that the median RRX estimate provides the least deviation from the truth for this sample size and data type. However, the MLE outputs are grouped more closely together, as evidenced by the bounds. The previous figures also show the simulation-based bounds, as well as the expected variation due to sampling error.

This experiment can be repeated in SimuMatic using multiple censoring schemes (including Type I and Type II right censoring as well as random censoring) with various distributions. Multiple experiments can be performed with this utility to evaluate assumptions about the appropriate parameter estimation method to use for data sets.