Repairable Systems Analysis Through Simulation
Having introduced some of the basic theory and terminology for repairable systems in Chapter 7, we will now examine the steps involved in the analysis of such complex systems. We will begin by examining system behavior through a sequence of discrete deterministic events and expand the analysis using discrete event simulation.
Simple Repairs
Deterministic View, Simple Series
To first understand how component failures and simple repairs affect the system and to visualize the steps involved, let's begin with a very simple deterministic example with two components, [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math], in series.
Component [math]\displaystyle{ A }[/math] fails every 100 hours and component [math]\displaystyle{ B }[/math] fails every 120 hours. Both require 10 hours to get repaired. Furthermore, assume that the surviving component stops operating when the system fails (thus not aging).
NOTE: When a failure occurs in certain systems, some or all of the system's components
may or may not continue to accumulate operating time while the system is down. For example,
consider a transmitter-satellite-receiver system. This is a series system and the probability
of failure for this system is the probability that any of the subsystems fail. If the receiver
fails, the satellite continues to operate even though the receiver is down. In this case, the
continued aging of the components during the system inoperation must be taken into
consideration, since this will affect their failure characteristics and have an impact on the
overall system downtime and availability.
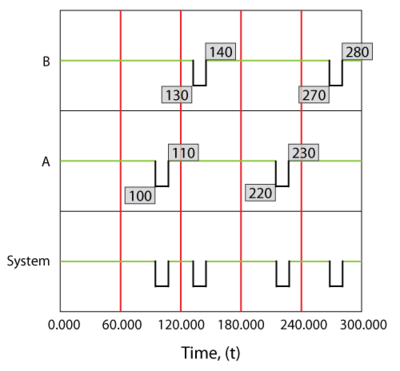
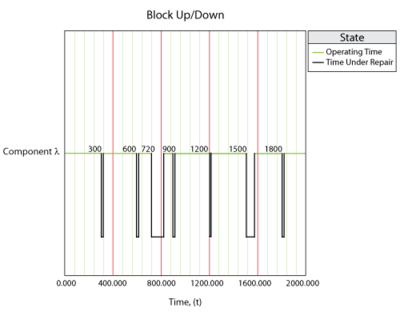
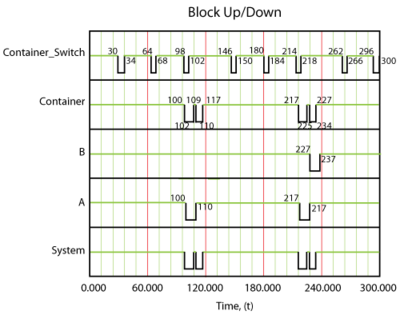
The system behavior during an operation from 0 to 300 hours would be as shown in Figure fig1.
Specifically, component [math]\displaystyle{ A }[/math] would fail at 100 hours, causing the system to fail. After 10 hours, component [math]\displaystyle{ A }[/math] would be restored and so would the system. The next event would be the failure of component [math]\displaystyle{ B }[/math] . We know that component [math]\displaystyle{ B }[/math] fails every 120 hours (or after an age of 120 hours). Since a component does not age while the system is down, component [math]\displaystyle{ B }[/math] would have reached an age of 120 when the clock reaches 130 hours. Thus, component [math]\displaystyle{ B }[/math] would fail at 130 hours and be repaired by 140 and so forth. Overall in this scenario, the system would be failed for a total of 40 hours due to four downing events (two due to [math]\displaystyle{ A }[/math] and two due to [math]\displaystyle{ B }[/math] ). The overall system availability (average or mean availability) would be [math]\displaystyle{ 260/300=0.86667 }[/math] . Point availability is the availability at a specific point time. In this deterministic case, the point availability would always be equal to 1 if the system is up at that time and equal to zero if the system is down at that time.
Operating Through System Failure
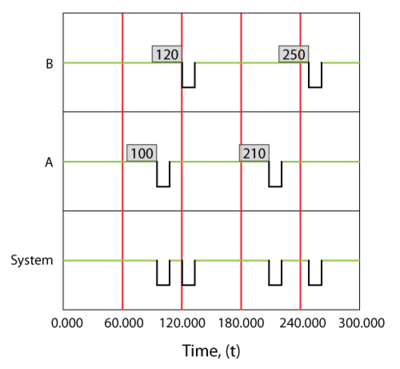
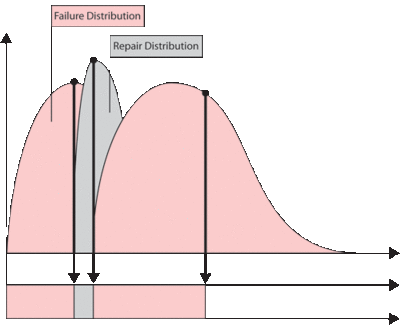
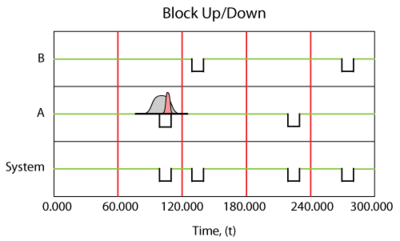
In the prior section we made the assumption that components do not age when the system is down. This assumption applies to most systems. However, under special circumstances, a unit may age even while the system is down. In such cases, the operating profile will be different from the one presented in the prior section. Figure fig2 illustrates the case where the components operate continuously, regardless of the system status.
Effects of Operating Through Failure
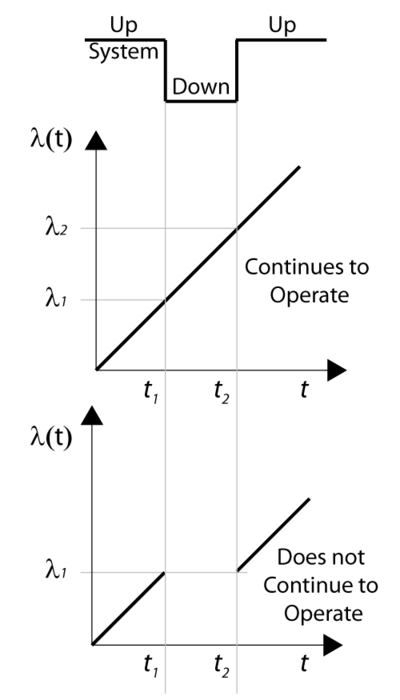
Consider a component with an increasing failure rate, as shown in Figure fig2a. In the case that the component continues to operate through system failure, then when the system fails at [math]\displaystyle{ {{t}_{1}} }[/math] the surviving component's failure rate will be [math]\displaystyle{ {{\lambda }_{1}} }[/math] , as illustrated in Figure fig2a. When the system is restored at [math]\displaystyle{ {{t}_{2}} }[/math] , the component would have aged by [math]\displaystyle{ {{t}_{2}}-{{t}_{1}} }[/math] and its failure rate would now be [math]\displaystyle{ {{\lambda }_{2}} }[/math] .
In the case of a component that does not operate through failure, then the surviving component would be at the same failure rate, [math]\displaystyle{ {{\lambda }_{1}}, }[/math] when the system resumes operation.
Deterministic View, Simple Parallel
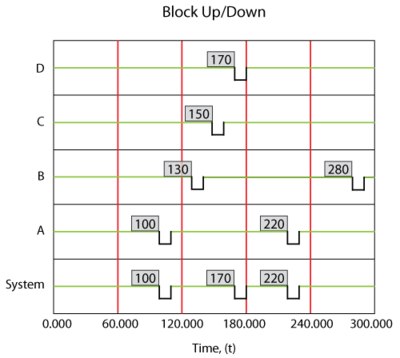
Consider the following system where [math]\displaystyle{ A }[/math] fails every 100, [math]\displaystyle{ B }[/math] every 120, [math]\displaystyle{ C }[/math] every 140 and [math]\displaystyle{ D }[/math] every 160 time units. Each takes 10 time units to restore. Furthermore, assume that components do not age when the system is down.
A deterministic system view is shown in Figure fig2a. The sequence of events is as follows:
- At 100, [math]\displaystyle{ A }[/math] fails and is repaired by 110. The system is failed.
- At 130, [math]\displaystyle{ B }[/math] fails and is repaired by 140. The system continues to operate.
- At 150, [math]\displaystyle{ C }[/math] fails and is repaired by 160. The system continues to operate.
- At 170, [math]\displaystyle{ D }[/math] fails and is repaired by 180. The system is failed.
- At 220, [math]\displaystyle{ A }[/math] fails and is repaired by 230. The system is failed.
- At 280, [math]\displaystyle{ B }[/math] fails and is repaired by 290. The system continues to operate.
- End at 300.
Additional Notes
It should be noted that we are dealing with these events deterministically in order to better illustrate the methodology. When dealing with deterministic events, it is possible to create a sequence of events that one would not expect to encounter probabilistically. One such example consists of two units in series that do not operate through failure but both fail at exactly 100, which is highly unlikely in a real-world scenario. In this case, the assumption is that one of the events must occur at least an infinitesimal amount of time ( [math]\displaystyle{ dt) }[/math] before the other. Probabilistically, this event is extremely rare, since both randomly generated times would have to be exactly equal to each other, to 15 decimal points. In the rare event that this happens, BlockSim would pick the unit with the lowest ID value as the first failure. BlockSim assigns a unique numerical ID when each component is created. These can be viewed by selecting the Show Block ID option in the Diagram Options window.
Deterministic Views of More Complex Systems
Even though the examples presented are fairly simplistic, the same approach can be repeated for larger and more complex systems. The reader can easily observe/visualize the behavior of more complex systems in BlockSim using the Up/Down plots. These are the same plots used in this chapter. It should be noted that BlockSim makes these plots available only when a single simulation run has been performed for the analysis (i.e. Number of Simulations = 1). These plots are meaningless when doing multiple simulations because each run will yield a different plot.
Probabilistic View, Simple Series
In a probabilistic case, the failures and repairs do not happen at a fixed time and for a fixed duration, but rather occur randomly and based on an underlying distribution, as shown in Figures Ch8fig3 and Ch8fig4.
We use discrete event simulation in order to analyze (understand) the system behavior. Discrete event simulation looks at each system/component event very similarly to the way we looked at these events in the deterministic example. However, instead of using deterministic (fixed) times for each event occurrence or duration, random times are used. These random times are obtained from the underlying distribution for each event. As an example, consider an event following a 2-parameter Weibull distribution. The [math]\displaystyle{ cdf }[/math] of the 2-parameter Weibull distribution is given by:
- [math]\displaystyle{ F(T)=1-{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}} }[/math]
The Weibull reliability function is given by:
- [math]\displaystyle{ \begin{align} R(T)= & 1-F(t) \\ = & {{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}} \end{align} }[/math]
Then, to generate a random time from a Weibull distribution with a given [math]\displaystyle{ \eta }[/math] and [math]\displaystyle{ \beta }[/math] , a uniform random number from 0 to 1, [math]\displaystyle{ {{U}_{R}}[0,1] }[/math] , is first obtained. The random time from a Weibull distribution is then obtained from:
- [math]\displaystyle{ {{T}_{R}}=\eta \cdot {{\left\{ -\ln \left[ {{U}_{R}}[0,1] \right] \right\}}^{\tfrac{1}{\beta }}} }[/math]
To obtain a conditional time, the Weibull conditional reliability function is given by:
- [math]\displaystyle{ R(T,t)=\frac{R(T+t)}{R(T)}=\frac{{{e}^{-{{\left( \tfrac{T+t}{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}}} }[/math]
- Or:
- [math]\displaystyle{ R(T,t)={{e}^{-\left[ {{\left( \tfrac{T+t}{\eta } \right)}^{\beta }}-{{\left( \tfrac{T}{\eta } \right)}^{\beta }} \right]}} }[/math]
The random time would be the solution for [math]\displaystyle{ t }[/math] for [math]\displaystyle{ R(T,t)={{U}_{R}}[0,1] }[/math] .
To illustrate the sequence of events, assume a single block with a failure and a repair distribution. The first event, [math]\displaystyle{ {{E}_{{{F}_{1}}}} }[/math] , would be the failure of the component. Its first time-to-failure would be a random number drawn from its failure distribution, [math]\displaystyle{ {{T}_{{{F}_{1}}}} }[/math] . Thus, the first failure event, [math]\displaystyle{ {{E}_{{{F}_{1}}}} }[/math] , would be at [math]\displaystyle{ {{T}_{{{F}_{1}}}} }[/math] . Once failed, the next event would be the repair of the component, [math]\displaystyle{ {{E}_{{{R}_{1}}}} }[/math] . The time to repair the component would now be drawn from its repair distribution, [math]\displaystyle{ {{T}_{{{R}_{1}}}} }[/math] . The component would be restored by time [math]\displaystyle{ {{T}_{{{F}_{1}}}}+{{T}_{{{R}_{1}}}} }[/math] . The next event would now be the second failure of the component after the repair, [math]\displaystyle{ {{E}_{{{F}_{2}}}} }[/math] . This event would occur after a component operating time of [math]\displaystyle{ {{T}_{{{F}_{2}}}} }[/math] after the item is restored (again drawn from the failure distribution), or at [math]\displaystyle{ {{T}_{{{F}_{1}}}}+{{T}_{{{R}_{1}}}}+{{T}_{{{F}_{2}}}} }[/math] . This process is repeated until the end time. It is important to note that each run will yield a different sequence of events due to the probabilistic nature of the times. To arrive at the desired result, this process is repeated many times and the results from each run (simulation) are recorded. In other words, if we were to repeat this 1,000 times, we would obtain 1,000 different values for [math]\displaystyle{ {{E}_{{{F}_{1}}}} }[/math] , or [math]\displaystyle{ \left[ {{E}_{{{F}_{{{1}_{1}}}}}},{{E}_{{{F}_{{{1}_{2}}}}}},...,{{E}_{{{F}_{{{1}_{1,000}}}}}} \right] }[/math].
The average of these values, [math]\displaystyle{ \left( \tfrac{1}{1000}\underset{i=1}{\overset{1,000}{\mathop{\sum }}}\,{{E}_{{{F}_{{{1}_{i}}}}}} \right) }[/math] , would then be the average time to the first event, [math]\displaystyle{ {{E}_{{{F}_{1}}}} }[/math] , or the mean time to first failure (MTTFF) for the component. Obviously, if the component were to be 100% renewed after each repair, then this value would also be the same for the second failure, etc.
General Simulation Results
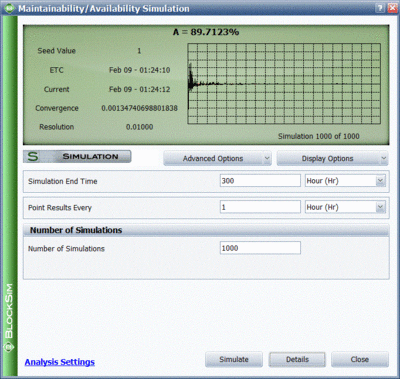
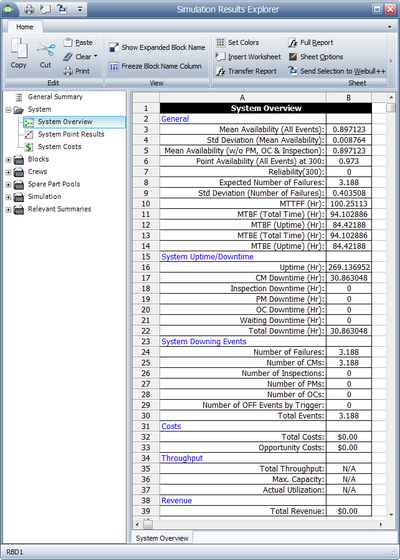
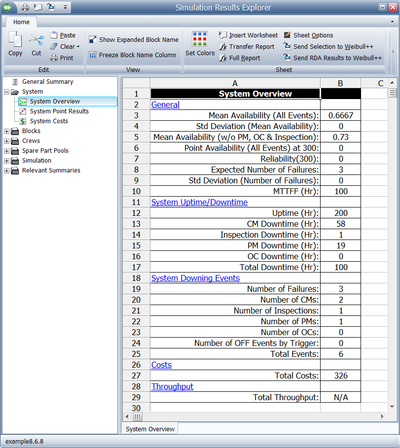
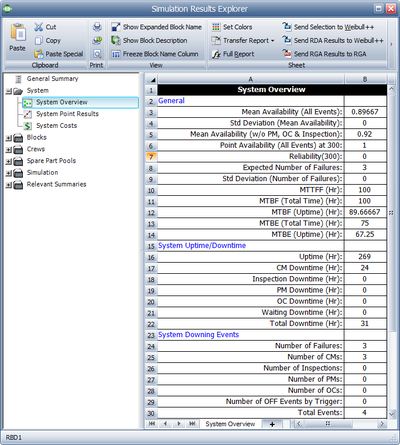
To further illustrate this, assume that both components in the prior example had normal failure and repair distributions with their means equal to the deterministic values used in the prior example and standard deviations of 10 and 1 respectively. That is, [math]\displaystyle{ {{F}_{A}}\tilde{\ }N(100,10), }[/math] [math]\displaystyle{ {{F}_{B}}\tilde{\ }N(120,10), }[/math] [math]\displaystyle{ {{R}_{A}}={{R}_{B}}\tilde{\ }N(10,1) }[/math] . Obviously, given the probabilistic nature of the example, the times to each event will vary. If one were to repeat this [math]\displaystyle{ X }[/math] number of times, one would arrive at the results of interest for the system and its components. Some of the results for this system and this example, over 1,000 simulations, are given in Figure Ch8fig6 and explained in the next sections. The simulation settings are shown in Figure Ch8fig5a.
General
Mean Availability (All Events), [math]\displaystyle{ {{\overline{A}}_{ALL}} }[/math]
This is the mean availability due to all downing events, which can be thought of as the operational availability. It is the ratio of the system uptime divided by the total simulation time (total time). For this example:
- [math]\displaystyle{ \begin{align} {{\overline{A}}_{ALL}}= & \frac{Uptime}{TotalTime} \\ = & \frac{260.386}{300} \\ = & 0.868 \end{align} }[/math]
Std Deviation (Mean Availability)
This is the standard deviation of the mean availability of all downing events for the system during the simulation.
Mean Availability (w/o PM & Inspection), [math]\displaystyle{ {{\overline{A}}_{CM}} }[/math]
This is the mean availability due to failure events only and it is 0.868 for this example. Note that for this case, the mean availability without preventive maintenance and inspection is identical to the mean availability for all events. This is because no preventive maintenance actions or inspections were defined for this system. We will discuss the inclusion of these actions in later sections.
Downtimes caused by PM and inspections are not included. However, if the PM or inspection action results in the discovery of a failure, then these times are included. As an example, consider a component that has failed but its failure is not discovered until the component is inspected. Then the downtime from the time failed to the time restored after the inspection is counted as failure downtime, since the original event that caused this was the component's failure.
Point Availability (All Events), [math]\displaystyle{ A\left( t \right) }[/math]
This is the probability that the system is up at time [math]\displaystyle{ t }[/math] . As an example, to obtain this value at [math]\displaystyle{ t }[/math] = 300, a special counter would need to be used during the simulation. This counter is increased by one every time the system is up at 300 hours. Thus, the point availability at 300 would be the times the system was up at 300 divided by the number of simulations. For this example, this is 0.930, or 930 times out of the 1000 simulations the system was up at 300 hours. Point Reliability (Fail Events), [math]\displaystyle{ R(t) }[/math].
This is the probability that the system has not failed by time [math]\displaystyle{ t }[/math] . This is similar to point availability with the major exception that it only looks at the probability that the system did not have a single failure. Other (non-failure) downing events are ignored. During the simulation, a special counter again must be used. This counter is increased by one (once in each simulation) if the system has had at least one failure up to 300 hours. Thus, the point reliability at 300 would be the number of times the system did not fail up to 300 divided by the number of simulations. For this example, this is 0 because the system failed prior to 300 hours 1000 times out of the 1000 simulations.
It is very important to note that this value is not always the same as the reliability computed using the analytical methods, depending on the redundancy present. The reason that it may differ is best explained by the following scenario:
Assume two units in parallel. The analytical system reliability, which does not account for repairs, is the probability that both units fail. In this case, when one unit goes down, it does not get repaired and the system fails after the second unit fails. In the case of repairs, however, it is possible for one of the two units to fail and get repaired before the second unit fails. Thus, when the second unit fails, the system will still be up due to the fact that the first unit was repaired.
Expected Number of Failures, [math]\displaystyle{ {{N}_{F}} }[/math]
This is the average number of system failures. The system failures (not downing events) for all simulations are counted and then averaged. For this case, this is 3.993, which implies that a total of 3,993 system failure events occurred over 1000 simulations. Thus, the expected number of system failures for one run is 3.993. This number includes all failures, even those that may have a duration of zero.
Std Deviation (Number of Failures)
This is the standard deviation of the number of failures for the system during the simulation.
MTTFF
MTTFF is the mean time to first failure for the system. This is computed by keeping track of the time at which the first system failure occurred for each simulation. MTTFF is then the average of these times. This may or may not be identical to the MTTF obtained in the analytical solution for the same reasons as those discussed in the Point Reliability section. For this case, this is 98.856. This is fairly obvious for this case since the mean of one of the components in series was 100 hours.
It is important to note that for each simulation run, if a first failure time is observed, then this is recorded as the system time to first failure. If no failure is observed in the system, then the simulation end time is used as a right censored (suspended) data point. MTTFF is then computed using the total operating time until the first failure divided by the number of observed failures (constant failure rate assumption). Furthermore, and if the simulation end time is much less than the time to first failure for the system, it is also possible that all data points are right censored (i.e. no system failures were observed). In this case, the MTTFF is again computed using a constant failure rate assumption, or:
- [math]\displaystyle{ MTTFF=\frac{2\cdot ({{T}_{S}})\cdot N}{\chi _{0.50;2}^{2}} }[/math]
Where [math]\displaystyle{ {{T}_{S}} }[/math] is the simulation end time and [math]\displaystyle{ N }[/math] is the number of simulations. One should be aware that this formulation may yield unrealistic (or erroneous) results if the system does not have a constant failure rate. If you are trying to obtain an accurate (realistic) estimate of this value, then your simulation end time should be set to a value that is well beyond the MTTF of the system (as computed analytically). As a general rule, the simulation end time should be at least three times larger than the MTTF of the system.
System Uptime/Downtime
Uptime, [math]\displaystyle{ {{T}_{UP}} }[/math]
This is the average time the system was up and operating. This is obtained by taking the sum of the uptimes for each simulation and dividing it by the number of simulations. For this example, the uptime is 260.386. To compute the Operational Availability, [math]\displaystyle{ {{A}_{o}}, }[/math] for this system, then:
- [math]\displaystyle{ {{A}_{o}}=\frac{{{T}_{UP}}}{{{T}_{S}}} }[/math]
CM Downtime, [math]\displaystyle{ {{T}_{C{{M}_{Down}}}} }[/math] This is the average time the system was down for corrective maintenance actions (CM) only. This is obtained by taking the sum of the CM downtimes for each simulation and dividing it by the number of simulations. For this example, this is 39.614. To compute the Inherent Availability, [math]\displaystyle{ {{A}_{I}}, }[/math] for this system over the observed time (which may or may not be steady state, depending on the length of the simulation), then:
- [math]\displaystyle{ {{A}_{I}}=\frac{{{T}_{S}}-{{T}_{C{{M}_{Down}}}}}{{{T}_{S}}} }[/math]
Inspection Downtime, ..
This is the average time the system was down due to inspections. This is obtained by taking the sum of the inspection downtimes for each simulation and dividing it by the number of simulations. For this example, this is zero because no inspections were defined.
PM Downtime, [math]\displaystyle{ {{T}_{P{{M}_{Down}}}} }[/math]
This is the average time the system was down due to preventive maintenance (PM) actions. This is obtained by taking the sum of the PM downtimes for each simulation and dividing it by the number of simulations. For this example, this is zero because no PM actions were defined.
Total Downtime, [math]\displaystyle{ {{T}_{Down}} }[/math]
This is the downtime due to all events. In general, one may look at this as the sum of the above downtimes. However, this is not always the case. It is possible to have actions that overlap each other, depending on the options and settings for the simulation. Furthermore, there are other events that can cause the system to go down that do not get counted in any of the above categories. As an example, in the case of standby redundancy with a switch delay, if the settings are to reactivate the failed component after repair, the system may be down during the switch-back action. This downtime does not fall into any of the above categories but it is counted in the total downtime.
For this example, this is identical to [math]\displaystyle{ {{T}_{C{{M}_{Down}}}}. }[/math]
System Downing Events
System downing events are events associated with downtime. If the duration of an event is zero, the event is not counted as a system downing event. However, the block properties CM brings system down, PM brings system down and Inspection brings system down take precedence in which case an event with zero duration will be counted as a system downing event.
Number of Failures (System Downing), [math]\displaystyle{ {{N}_{{{F}_{Down}}}} }[/math]
This is the average number of system downing failures. Unlike the Expected Number of Failures, [math]\displaystyle{ {{N}_{F}}, }[/math] this number does not include failures with zero duration. For this example, this is 3.993.
Number of CMs (System Downing), [math]\displaystyle{ {{N}_{C{{M}_{Down}}}} }[/math]
This is the number of corrective maintenance actions that caused the system to fail. It is obtained by taking the sum of all CM actions that caused the system to fail divided by the number of simulations. It does not include CM events of zero duration. For this example, this is 3.993. Note that this may differ from the Number of Failures (System Downing), [math]\displaystyle{ {{N}_{{{F}_{Down}}}} }[/math] . An example would be a case where the system has failed, but due to other settings for the simulation, a CM is not initiated (e.g. an inspection is needed to initiate a CM).
Number of Inspections (System Downing), [math]\displaystyle{ {{N}_{{{I}_{Down}}}} }[/math]
This is the number of inspection actions that caused the system to fail. It is obtained by taking the sum of all inspection actions that caused the system to fail divided by the number of simulations. It does not include inspection events of zero duration. For this example, this is zero.
Number of PMs (System Downing), [math]\displaystyle{ {{N}_{P{{M}_{Down}}}} }[/math]
This is the number of PM actions that caused the system to fail. It is obtained by taking the sum of all PM actions that caused the system to fail divided by the number of simulations. It does not include PM events of zero duration. For this example, this is zero.
Total Events (System Downing), [math]\displaystyle{ {{N}_{AL{{L}_{Down}}}} }[/math]
This is the total number of system downing events. It also does not include events of zero duration. It is possible that this number may differ from the sum of the other listed events. As an example, consider the case where a failure does not get repaired until an inspection, but the inspection occurs after the simulation end time. In this case, the number of inspections, CMs and PMs will be zero while the number of total events will be one.
Costs and Throughput
Cost and throughput results are discussed in later sections.
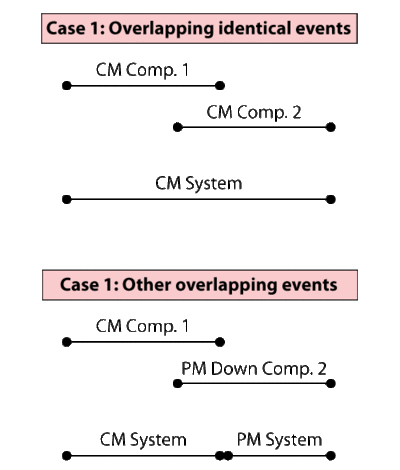
Note About Overlapping Downing Events
It is important to note that two identical system downing events (that are continuous or overlapping) may be counted and viewed differently. As shown in Case 1 of Figure fig7, two overlapping failure events are counted as only one event from the system perspective because the system was never restored and remained in the same down state, even though that state was caused by two different components. Thus, the number of downing events in this case is one and the duration is as shown in CM system. In the case that the events are different, as shown in Case 2 of Figure fig7, two events are counted, the CM and the PM. However, the downtime attributed to each event is different from the actual time of each event. In this case, the system was first down due to a CM and remained in a down state due to the CM until that action was over. However, immediately upon completion of that action, the system remained down but now due to a PM action. In this case, only the PM action portion that kept the system down is counted.
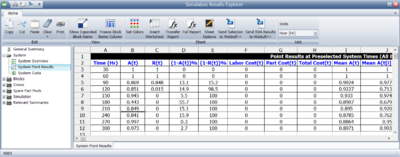
System Point Result
The system point results, as shown in Figure fig8, shows the Point Availability (All Events), [math]\displaystyle{ A\left( t \right) }[/math] , and Point Reliability, [math]\displaystyle{ R(t) }[/math] , as defined in the previous section. These are computed and returned at different points in time, based on the number of intervals selected by the user. Additionally, this window shows [math]\displaystyle{ (1-A\left( t \right)) }[/math] , [math]\displaystyle{ (1-R(t)) }[/math] , [math]\displaystyle{ Cost(t) }[/math] , [math]\displaystyle{ Mean }[/math] [math]\displaystyle{ A(t) }[/math] , [math]\displaystyle{ Mean }[/math] [math]\displaystyle{ A({{t}_{i}}-{{t}_{i-1}}) }[/math] , [math]\displaystyle{ System }[/math] [math]\displaystyle{ Failures(t) }[/math] , and [math]\displaystyle{ Throughput(t) }[/math] .
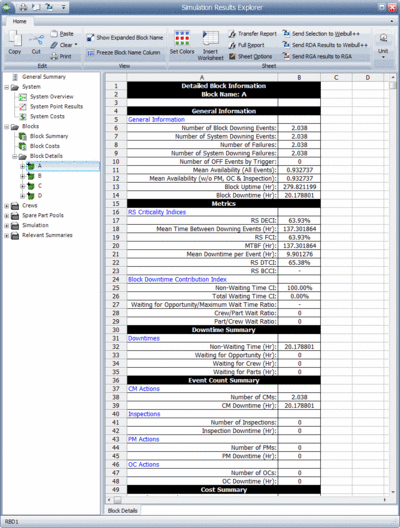
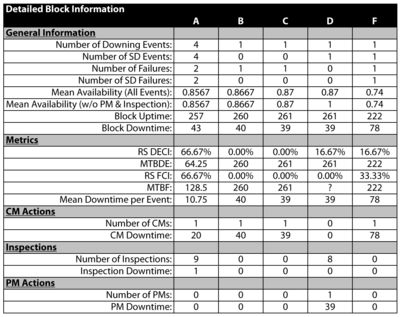
Results by Component
Simulation results for each component can also be viewed. Figure fig9 shows the results for component A. These results are explained in the sections that follow.
General Information
Number of Downing Events, [math]\displaystyle{ Componen{{t}_{NDE}} }[/math]
This the number of times the component went down (failed). It includes all downing events.
Number of SD Events, [math]\displaystyle{ Componen{{t}_{NSDE}} }[/math]
This is the number of times that this component's downing caused the system to be down. For component [math]\displaystyle{ A }[/math] , this is 2.011. Note that this value is the same in this case as the number of component failures, since the two components are reliability-wise in series. If this were not the case (e.g. if they were in a parallel configuration), this value would be different.
Number of Failures, [math]\displaystyle{ Componen{{t}_{NF}} }[/math]
This is the number of times the component failed and does not include other downing events. Note that this could also be interpreted as the number of spare parts required for CM actions for this component. For component [math]\displaystyle{ A }[/math] , this is 2.011.
Number of SD Failures, [math]\displaystyle{ Componen{{t}_{NSDF}} }[/math]
This is the number of times that this component's failure caused the system to be down. Note that this may be different from the Number of SD Events. It only counts the failure events that downed the system and does not include zero duration system failures.
Mean Availability (All Events), [math]\displaystyle{ {{\overline{A}}_{AL{{L}_{Component}}}} }[/math]
This has the same definition as for the system with the exception that this accounts only for the component.
Mean Availability (w/o PM & Inspection), [math]\displaystyle{ {{\overline{A}}_{C{{M}_{Component}}}} }[/math]
This has the same definition as for the system with the exception that this accounts only for the component.
Block Uptime, [math]\displaystyle{ {{T}_{Componen{{t}_{UP}}}} }[/math]
This is the average time the component was up. For component [math]\displaystyle{ A }[/math] , this is 279.9651.
Block Downtime, [math]\displaystyle{ {{T}_{Componen{{t}_{Down}}}} }[/math]
This is the average time the component was down for any reason. For component [math]\displaystyle{ A }[/math] , this is 20.0349.
Metrics
RS DECI
ReliaSoft's Downing Event Criticality Index (RS DECI) is a relative index showing the percentage of times that a downing event of this component caused the system to go down. For component [math]\displaystyle{ A }[/math] , this is 50.36%. This implies that 50.36% of the times that the system went down, the system failure was due to the fact that component [math]\displaystyle{ A }[/math] went down. This is obtained from:
- [math]\displaystyle{ RSDECI=\frac{Componen{{t}_{NSDE}}}{{{N}_{AL{{L}_{Down}}}}} }[/math]
MTBDE
This is the mean time between downing events of the component, which is computed from:
- [math]\displaystyle{ MTBDE=\frac{{{T}_{Componen{{t}_{UP}}}}}{Componen{{t}_{NDE}}} }[/math]
For component [math]\displaystyle{ A }[/math] , this is 139.2168.
RS FCI
ReliaSoft's Failure Criticality Index (RS FCI) is a relative index showing the percentage of times that a failure of this component caused a system failure. For component [math]\displaystyle{ A }[/math] , this is 50.36%. This implies that 50.36% of the times that the system failed, it was due to the fact that component [math]\displaystyle{ A }[/math] failed. This is obtained from:
- [math]\displaystyle{ RSFCI=\frac{Componen{{t}_{NSDF}}+{{F}_{ZD}}}{{{N}_{F}}} }[/math]
[math]\displaystyle{ {{F}_{ZD}} }[/math] is a special counter of system failures not included in [math]\displaystyle{ Componen{{t}_{NSDF}} }[/math] . This counter is not explicitly shown in the results but is maintained by the software. The reason for this counter is the fact that zero duration failures are not counted in [math]\displaystyle{ Componen{{t}_{NSDF}} }[/math] since they really did not down the system. However, these zero duration failures need to be included when computing RS FCI.
It is important to note that for both RS DECI and RS FCI, and if overlapping events are present, the component that caused the system event gets credited with the system event. Subsequent component events that do not bring the system down (since the system is already down) do not get counted in this metric.
MTBF, [math]\displaystyle{ MTB{{F}_{C}} }[/math]
Mean time between failures is the mean (average) time between failures of this component, in real clock time. This is computed from:
- [math]\displaystyle{ MTB{{F}_{C}}=\frac{{{T}_{S}}-CFDowntime}{Componen{{t}_{NF}}} }[/math]
[math]\displaystyle{ CFDowntime }[/math] is the downtime of the component due to failures only (without PM and inspection). The discussion regarding what is a failure downtime that was presented in the section explaining Mean Availability (w/o PM & Inspection) also applies here.
For component [math]\displaystyle{ A }[/math] , this is 139.2168. Note that this value could fluctuate for the same component depending on the simulation end time. As an example, consider the deterministic scenario for this component. It fails every 100 hours and takes 10 hours to repair. Thus, it would be failed at 100, repaired by 110, failed at 210 and repaired by 220. Therefore, its uptime is 280 with two failure events, MTBF = 280/2 = 140. Repeating the same scenario with an end time of 330 would yield failures at 100, 210 and 320. Thus, the uptime would be 300 with three failures, or MTBF = 300/3 = 100. Note that this is not the same as the MTTF (mean time to failure), commonly referred to as MTBF by many practitioners.
Mean Downtime per Event, [math]\displaystyle{ MDPE }[/math]
Mean downtime per event is the average downtime for a component event. This is computed from:
- [math]\displaystyle{ MDPE=\frac{{{T}_{Componen{{t}_{Down}}}}}{Componen{{t}_{NDE}}} }[/math]
Other Results of Interest
The remaining component (block) results are similar to those defined for the system with the exception that now they apply only to the component.
Imperfect Repairs
Restoration Factors (RF)
In the prior discussion it was assumed that a repaired component is as good as new after repair. This is usually the case when replacing a component with a new one. The concept of a restoration factor may be used in cases in which one wants to model imperfect repair, or a repair with a used component. The best way to indicate that a component is not as good as new is to give the component some age. As an example, if one is dealing with car tires, a tire that is not as good as new would have some pre-existing wear on it. In other words, the tire would have some accumulated mileage. A restoration factor concept is used to better describe the existing age of a component. The restoration factor is used to determine the age of the component after a repair or any other maintenance action (addressed in later sections, such as a PM action or inspection).
The restoration factor in BlockSim is defined as a number between 0 and 1 and has the following effect:
- A restoration factor of 1 (100%) implies that the component is as good as new after repair, which in effect implies that the starting age of the component is 0.
- A restoration factor of 0 implies that the component is the same as it was prior to repair, which in effect implies that the starting age of the component is the same as the age of the component at failure.
- A restoration factor of 0.25 (25%) implies that the starting age of the component is equal to 75% of the age of the component at failure.
Figure figrestore provides a visual demonstration of restoration factors. It should be noted that for successive maintenance actions on the same component, the age of the component after such an action is the initial age plus the time to failure since the last maintenance action.
Type I and Type II RFs
BlockSim 7 offers two kinds of restoration factors. The type I restoration factor is based on Kijima [12, 13] model I and assumes that the repairs can only fix the wear-out and damage incurred during the last period of operation. Thus, the nth repair can only remove the damage incurred during the time between the (n-1)th and nth failures. The type II restoration factor, based on Kijima model II, assumes that the repairs fix all of the wear-out and damage accumulated up to the current time. As a result, the nth repair not only removes the damage incurred during the time between the (n-1)th and nth failures, but can also fix the cumulative damage incurred during the time from the first failure to the (n-1)th failure.
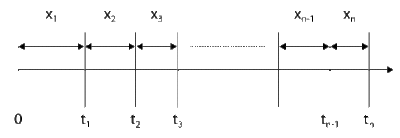
To illustrate this, consider a repairable system, observed from time [math]\displaystyle{ t=0 }[/math] , as shown in Figure RFInIIsys. Let the successive failure times be denoted by [math]\displaystyle{ {{t}_{1}} }[/math] , [math]\displaystyle{ {{t}_{2}} }[/math] , ... and let the times between failures be denoted by [math]\displaystyle{ {{x}_{1}} }[/math] , [math]\displaystyle{ {{x}_{2}} }[/math] , .... Let [math]\displaystyle{ RF }[/math] denote the restoration factor, then the age of the system [math]\displaystyle{ {{v}_{n}} }[/math] at time [math]\displaystyle{ {{t}_{n}} }[/math] using the two types of restoration factors is:
Type I Restoration Factor:
- [math]\displaystyle{ {{v}_{n}}={{v}_{n-1}}+(1-RF){{x}_{n}} }[/math]
Type II Restoration Factor:
- [math]\displaystyle{ {{v}_{n}}=(1-RF)({{v}_{n-1}}+{{x}_{n}}) }[/math]
Illustrating Type I RF Through an Example
Assume that you have a component with a Weibull failure distribution ( [math]\displaystyle{ \beta =1.5 }[/math] , [math]\displaystyle{ \eta =1000 }[/math] [math]\displaystyle{ hr }[/math] ), RF type I = 0.25 and the component undergoes instant repair. Furthermore, assume that the component starts life new (i.e. with a start age of zero). The simulation steps are as follows:
- Generate a uniform random number, [math]\displaystyle{ {{U}_{R}}[0,1] }[/math] = 0.7021885.
- The first failure event will then be at 500 hrs.
- After instantaneous repair, the component will begin life with an age after repair of 350 hrs [math]\displaystyle{ (500\times (1-0.25)) }[/math] .
- Generate another uniform random number, [math]\displaystyle{ {{U}_{R}}[0,1] }[/math] = 0.8824969.
- The next failure event is now determined using the conditional reliability equation, or:
- Generate a uniform random number, [math]\displaystyle{ {{U}_{R}}[0,1] }[/math] = 0.7021885.
- [math]\displaystyle{ \begin{align} R(t+T)= & R(t,T)\cdot R(T) \\ R(t+350)= & 0.8824969\cdot R(350) \\ R(t+350)= & 0.8824969\cdot 0.8129686 \\ R(t+350)= & 0.71744226 \\ t+350= & 479.527 \\ t = & 129.527 \end{align} }[/math]
Thus, the next failure event will be at [math]\displaystyle{ 500+129.527=629.527 }[/math] hrs. Note that if the component had been as good as new (i.e. RF = 100%), then the next failure would have been at 750 hrs (500 + 250), where 250 is the time corresponding to a reliability of 0.8824969, which is the random number that was generated in Step 4.
- 6. At this failure point, the item's age will now be equal to the initial age, after the first corrective action, plus the additional time it operated, or [math]\displaystyle{ 350+129.527 }[/math] hrs.
- 7. Thus, the age after the second repair will be the sum of the previous age and the restoration factor times the age of the component since the last failure, or [math]\displaystyle{ 350+(129.527\times (1-0.25))=447.14525 }[/math] hrs.
- 8. Go to Step 4 and repeat the process.
Illustrating Type II RF Through an Example
Assume that you have a component with a Weibull failure distribution ( [math]\displaystyle{ \beta =1.5 }[/math] , [math]\displaystyle{ \eta =1000 }[/math] [math]\displaystyle{ hr }[/math] ), RF type II = 0.25 and the component undergoes instant repair. Furthermore, assume that the component starts life new (i.e. with a start age of zero). The simulation steps are as follows:
- Generate a uniform random number, [math]\displaystyle{ {{U}_{R}}[0,1] }[/math] = 0.7021885.
- The first failure event will then be at 500 hrs.
- After instantaneous repair, the component will begin life with an age after repair of 350 hrs [math]\displaystyle{ (500\times (1-0.25)) }[/math] .
- Generate another uniform random number, [math]\displaystyle{ {{U}_{R}}[0,1] }[/math] = 0.8824969.
- The next failure event is now determined using the conditional reliability equation, or:
- Generate a uniform random number, [math]\displaystyle{ {{U}_{R}}[0,1] }[/math] = 0.7021885.
- [math]\displaystyle{ \begin{align} R(t+T)= & R(t,T)\cdot R(T) \\ R(t+350)= & 0.8824969\cdot R(350) \\ R(t+350)= & 0.8824969\cdot 0.8129686 \\ R(t+350)= & 0.71744226 \\ t+350= & 479.527 \\ t= & 129.527 \end{align} }[/math]
Thus, the next failure event will be at [math]\displaystyle{ 500+129.527=629.527 }[/math] hrs. Note that if the component had been as good as new (i.e. RF = 100%), then the next failure would have been at 750 hrs (500 + 250), where 250 is the time corresponding to a reliability of 0.8824969, which is the random number that was generated in Step 4.
- 6. At this failure point, the item's age will now be equal to the initial age, after the first corrective action, plus the additional time it operated, or [math]\displaystyle{ 350+129.527 }[/math] .
- 7. Thus, the age after the second repair will be the restoration factor times the age of the component at failure, or [math]\displaystyle{ (350+129.527)\times (1-0.25)=359.64525 }[/math] hrs.
- 8. Go to Step 4 and repeat the process.
Discussion of Type I and Type II RFs
As an application example, consider an automotive engine that fails after six years of operation. The engine is rebuilt. The rebuild has the effect of rejuvenating the engine to a condition as if it were three years old (i.e. a 50% RF). Assume that the rebuild affects all of the damage on the engine (i.e. a Type II restoration). The engine fails again after three years (when it again reaches an age of six) and another rebuild is required. This rebuild will also rejuvenate the engine by 50%, thus making it three years old again.
Now consider a similar engine subjected to a similar rebuild, but that the rebuild only affects the damage since the last repair (i.e. a Type I restoration of 50%). The first rebuild will rejuvenate the engine to a three-year-old condition. The engine will fail again after three years, but the rebuild this time will only affect the age (of three years) after the first rebuild. Thus the engine will have an age of four and a half years after the second rebuild ( [math]\displaystyle{ 3+3\times (1-0.5)=4.5 }[/math] ). After the second rebuild the engine will fail again after a period of one and a half years and a third rebuild will be required. The age of the engine after the third rebuild will be five years and three months ( [math]\displaystyle{ 4.5+1.5\times (1-0.5)=5.25 }[/math] ).
It should be pointed out that when dealing with constant failure rates (i.e. with a distribution such as the exponential), the restoration factor has no effect.
Calculations to obtain RFs
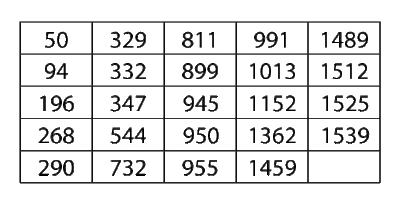
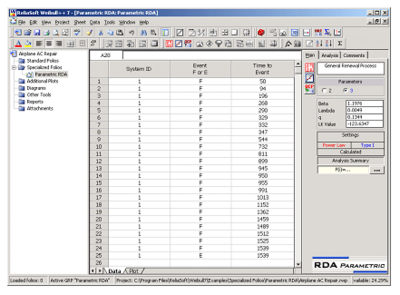
The two types of restoration factors discussed in the previous sections can be calculated using the parametric RDA (Recurrent Data Analysis) tool in Weibull++ 7. This tool uses the GRP (General Renewal Process) model to analyze failure data of a repairable item. More information on the Parametric RDA tool and the GRP (General Renewal Process) model can be found in [25]. As an example, consider the times to failure for an air-conditioning unit of an aircraft recorded in the following table. Assume that each time the unit is repaired, the repair can only remove the damage incurred during the last period of operation. This assumption implies a type I RF factor which is specified as an analysis setting in the Weibull++ folio. The type I RF for the air-conditioning unit can be calculated using the results from Weibull++ shown in Figure RFtypeIRDAEx.
The value of the action effectiveness factor [math]\displaystyle{ q }[/math] obtained from Weibull++ is:
- [math]\displaystyle{ q=0.1344 }[/math]
The type I RF factor is calculated using [math]\displaystyle{ q }[/math] as:
- [math]\displaystyle{ \begin{align} RF= & 1-q \\ = & 1-0.1344 \\ = & 0.8656 \end{align} }[/math]
The parameters of the Weibull distribution for the air-conditioning unit can also be calculated. [math]\displaystyle{ \beta }[/math] is obtained from Weibull++ as 1.1976. [math]\displaystyle{ \eta }[/math] can be calculated using the [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \lambda }[/math] values from Weibull++ as:
- [math]\displaystyle{ \begin{align} \eta = & {{\left( \frac{1}{\lambda } \right)}^{\tfrac{1}{\beta }}} \\ = & {{\left( \frac{1}{0.0049} \right)}^{\tfrac{1}{1.1976}}} \\ = & 84.8582 \end{align} }[/math]
The values of the type I RF, [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \eta }[/math] calculated above can now be used to model the air-conditioning unit as a component in BlockSim.
Type I and Type II RFs
BlockSim 7 offers two kinds of restoration factors. The type I restoration factor is based on Kijima [12, 13] model I and assumes that the repairs can only fix the wear-out and damage incurred during the last period of operation. Thus, the nth repair can only remove the damage incurred during the time between the (n-1)th and nth failures. The type II restoration factor, based on Kijima model II, assumes that the repairs fix all of the wear-out and damage accumulated up to the current time. As a result, the nth repair not only removes the damage incurred during the time between the (n-1)th and nth failures, but can also fix the cumulative damage incurred during the time from the first failure to the (n-1)th failure.
[math]\displaystyle{ }[/math]
To illustrate this, consider a repairable system, observed from time [math]\displaystyle{ t=0 }[/math] , as shown in Figure RFInIIsys. Let the successive failure times be denoted by [math]\displaystyle{ {{t}_{1}} }[/math] , [math]\displaystyle{ {{t}_{2}} }[/math] , ... and let the times between failures be denoted by [math]\displaystyle{ {{x}_{1}} }[/math] , [math]\displaystyle{ {{x}_{2}} }[/math] , .... Let [math]\displaystyle{ RF }[/math] denote the restoration factor, then the age of the system [math]\displaystyle{ {{v}_{n}} }[/math] at time [math]\displaystyle{ {{t}_{n}} }[/math] using the two types of restoration factors is:
Type I Restoration Factor:
- [math]\displaystyle{ {{v}_{n}}={{v}_{n-1}}+(1-RF){{x}_{n}} }[/math]
Type II Restoration Factor:
- [math]\displaystyle{ {{v}_{n}}=(1-RF)({{v}_{n-1}}+{{x}_{n}}) }[/math]
Illustrating Type I RF Through an Example
Assume that you have a component with a Weibull failure distribution ( [math]\displaystyle{ \beta =1.5 }[/math] , [math]\displaystyle{ \eta =1000 }[/math] [math]\displaystyle{ hr }[/math] ), RF type I = 0.25 and the component undergoes instant repair. Furthermore, assume that the component starts life new (i.e. with a start age of zero). The simulation steps are as follows:
- Generate a uniform random number, [math]\displaystyle{ {{U}_{R}}[0,1] }[/math] = 0.7021885.
- The first failure event will then be at 500 hrs.
- After instantaneous repair, the component will begin life with an age after repair of 350 hrs [math]\displaystyle{ (500\times (1-0.25)) }[/math] .
- Generate another uniform random number, [math]\displaystyle{ {{U}_{R}}[0,1] }[/math] = 0.8824969.
- The next failure event is now determined using the conditional reliability equation, or:
- [math]\displaystyle{ \begin{align} R(t+T)= & R(t,T)\cdot R(T) \\ R(t+350)= & 0.8824969\cdot R(350) \\ R(t+350)= & 0.8824969\cdot 0.8129686 \\ R(t+350)= & 0.71744226 \\ t+350= & 479.527 \\ t= & 129.527 \end{align} }[/math]
Thus, the next failure event will be at [math]\displaystyle{ 500+129.527=629.527 }[/math] hrs. Note that if the component had been as good as new (i.e. RF = 100%), then the next failure would have been at 750 hrs (500 + 250), where 250 is the time corresponding to a reliability of 0.8824969, which is the random number that was generated in Step 4.
- 6. At this failure point, the item's age will now be equal to the initial age, after the first corrective action, plus the additional time it operated, or [math]\displaystyle{ 350+129.527 }[/math] hrs.
- 7. Thus, the age after the second repair will be the sum of the previous age and the restoration factor times the age of the component since the last failure, or [math]\displaystyle{ 350+(129.527\times (1-0.25))=447.14525 }[/math] hrs.
- 8. Go to Step 4 and repeat the process.
Illustrating Type II RF Through an Example
Assume that you have a component with a Weibull failure distribution ( [math]\displaystyle{ \beta =1.5 }[/math] , [math]\displaystyle{ \eta =1000 }[/math] [math]\displaystyle{ hr }[/math] ), RF type II = 0.25 and the component undergoes instant repair. Furthermore, assume that the component starts life new (i.e. with a start age of zero). The simulation steps are as follows:
- Generate a uniform random number, [math]\displaystyle{ {{U}_{R}}[0,1] }[/math] = 0.7021885.
- The first failure event will then be at 500 hrs.
- After instantaneous repair, the component will begin life with an age after repair of 350 hrs [math]\displaystyle{ (500\times (1-0.25)) }[/math] .
- Generate another uniform random number, [math]\displaystyle{ {{U}_{R}}[0,1] }[/math] = 0.8824969.
- The next failure event is now determined using the conditional reliability equation, or:
- [math]\displaystyle{ \begin{align} R(t+T)= & R(t,T)\cdot R(T) \\ R(t+350)= & 0.8824969\cdot R(350) \\ R(t+350)= & 0.8824969\cdot 0.8129686 \\ R(t+350)= & 0.71744226 \\ t+350= & 479.527 \\ t= & 129.527 \end{align} }[/math]
Thus, the next failure event will be at [math]\displaystyle{ 500+129.527=629.527 }[/math] hrs. Note that if the component had been as good as new (i.e. RF = 100%), then the next failure would have been at 750 hrs (500 + 250), where 250 is the time corresponding to a reliability of 0.8824969, which is the random number that was generated in Step 4.
- 6. At this failure point, the item's age will now be equal to the initial age, after the first corrective action, plus the additional time it operated, or [math]\displaystyle{ 350+129.527 }[/math] .
- 7. Thus, the age after the second repair will be the restoration factor times the age of the component at failure, or [math]\displaystyle{ (350+129.527)\times (1-0.25)=359.64525 }[/math] hrs.
- 8. Go to Step 4 and repeat the process.
Discussion of Type I and Type II RFs
As an application example, consider an automotive engine that fails after six years of operation. The engine is rebuilt. The rebuild has the effect of rejuvenating the engine to a condition as if it were three years old (i.e. a 50% RF). Assume that the rebuild affects all of the damage on the engine (i.e. a Type II restoration). The engine fails again after three years (when it again reaches an age of six) and another rebuild is required. This rebuild will also rejuvenate the engine by 50%, thus making it three years old again.
Now consider a similar engine subjected to a similar rebuild, but that the rebuild only affects the damage since the last repair (i.e. a Type I restoration of 50%). The first rebuild will rejuvenate the engine to a three-year-old condition. The engine will fail again after three years, but the rebuild this time will only affect the age (of three years) after the first rebuild. Thus the engine will have an age of four and a half years after the second rebuild ( [math]\displaystyle{ 3+3\times (1-0.5)=4.5 }[/math] ). After the second rebuild the engine will fail again after a period of one and a half years and a third rebuild will be required. The age of the engine after the third rebuild will be five years and three months ( [math]\displaystyle{ 4.5+1.5\times (1-0.5)=5.25 }[/math] ).
It should be pointed out that when dealing with constant failure rates (i.e. with a distribution such as the exponential), the restoration factor has no effect.
Calculations to obtain RFs
The two types of restoration factors discussed in the previous sections can be calculated using the parametric RDA (Recurrent Data Analysis) tool in Weibull++ 7. This tool uses the GRP (General Renewal Process) model to analyze failure data of a repairable item. More information on the Parametric RDA tool and the GRP (General Renewal Process) model can be found in [25]. As an example, consider the times to failure for an air-conditioning unit of an aircraft recorded in the following table. Assume that each time the unit is repaired, the repair can only remove the damage incurred during the last period of operation. This assumption implies a type I RF factor which is specified as an analysis setting in the Weibull++ folio. The type I RF for the air-conditioning unit can be calculated using the results from Weibull++ shown in Figure RFtypeIRDAEx.
The value of the action effectiveness factor [math]\displaystyle{ q }[/math] obtained from Weibull++ is:
- [math]\displaystyle{ q=0.1344 }[/math]
The type I RF factor is calculated using [math]\displaystyle{ q }[/math] as:
- [math]\displaystyle{ \begin{align} RF= & 1-q \\ = & 1-0.1344 \\ = & 0.8656 \end{align} }[/math]
The parameters of the Weibull distribution for the air-conditioning unit can also be calculated. [math]\displaystyle{ \beta }[/math] is obtained from Weibull++ as 1.1976. [math]\displaystyle{ \eta }[/math] can be calculated using the [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \lambda }[/math] values from Weibull++ as:
- [math]\displaystyle{ \begin{align} \eta = & {{\left( \frac{1}{\lambda } \right)}^{\tfrac{1}{\beta }}} \\ = & {{\left( \frac{1}{0.0049} \right)}^{\tfrac{1}{1.1976}}} \\ = & 84.8582 \end{align} }[/math]
The values of the type I RF, [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \eta }[/math] calculated above can now be used to model the air-conditioning unit as a component in BlockSim.
Using Resources: Pools and Crews
In order to make the analysis more realistic, one may wish to consider additional sources of delay times in the analysis or study the effect of limited resources. In the prior examples, we used a repair distribution to identify how long it takes to restore a component. The factors that one chooses to consider in this time may include the time it takes to do the repair and/or the time it takes to get a crew, a spare part, etc. While all of these factors may be included in the repair duration, optimized usage of these resources can only be achieved if the resources are studied individually and their dependencies are identified.
As an example, consider the situation where two components in parallel fail at the same time and only a single repair person is available. Because this person would not be able to execute the repair on both components simultaneously, an additional delay will be encountered that also needs to be included in the modeling. One way to accomplish this is to assign a specific repair crew to each component.
Including Crews
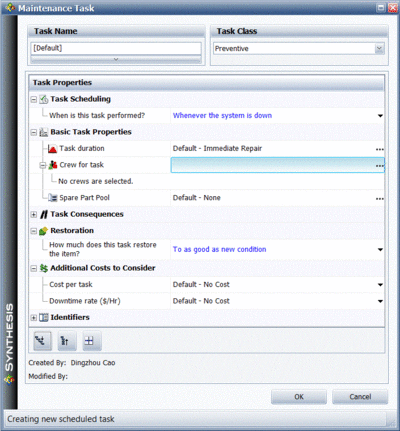
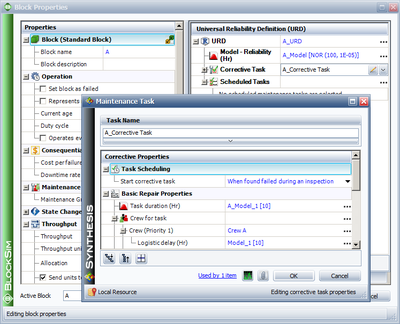
BlockSim allows you to assign maintenance crews to each component and one or more crews may be assigned to each component from the Block Properties window, as shown in Figure figcrew. Note that there may be different crews for each action, i.e. corrective, preventive, inspection.
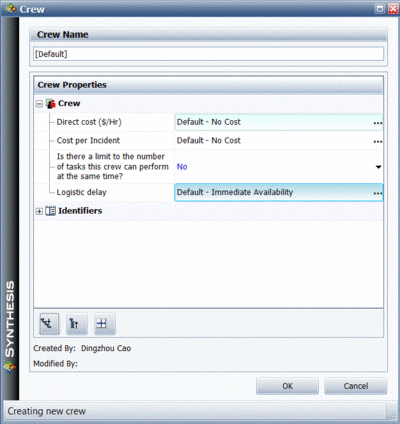
A policy needs to be defined for each named crew, as shown in Figure figcrewdefine. This policy identifies basic properties for the crew, such as:
- • Logistic delays. How long does it take for the crew to arrive?
- • How many simultaneous tasks can the crew perform?
- • What is the cost per hour for the crew?
- • Is there an additional cost per incident?
Illustrating Crew Use
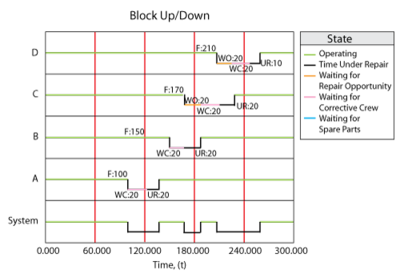
To illustrate the use of crews in BlockSim, consider the deterministic scenario described by the following RBD and properties.
Unit Failure Repair Crew
[math]\displaystyle{ A }[/math] [math]\displaystyle{ 100 }[/math] [math]\displaystyle{ 10 }[/math] Crew [math]\displaystyle{ A }[/math] : Delay = 20, Single Task
[math]\displaystyle{ B }[/math] [math]\displaystyle{ 120 }[/math] [math]\displaystyle{ 20 }[/math] Crew [math]\displaystyle{ A }[/math] : Delay = 20, Single Task
[math]\displaystyle{ C }[/math] [math]\displaystyle{ 140 }[/math] [math]\displaystyle{ 20 }[/math] Crew [math]\displaystyle{ A }[/math] : Delay = 20, Single Task
[math]\displaystyle{ D }[/math] [math]\displaystyle{ 160 }[/math] [math]\displaystyle{ 10 }[/math] Crew [math]\displaystyle{ A }[/math] : Delay = 20, Single Task
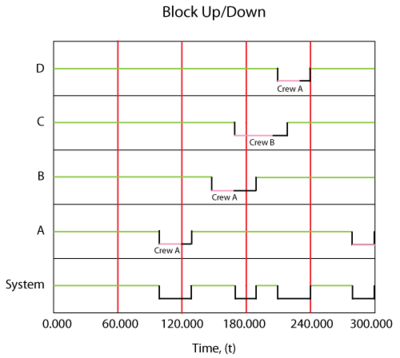
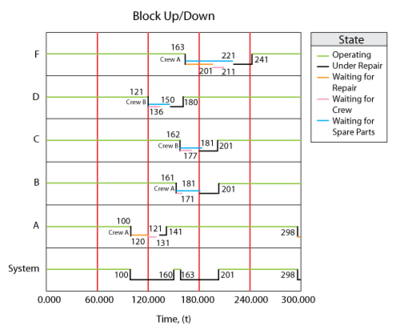
The System Up/Down plot in Figure figrewupdown illustrates the sequence of events, which are:
- At 100, [math]\displaystyle{ A }[/math] fails. It takes 20 to get the crew and 10 to repair, thus the component is repaired by 130. The system is failed/down during this time.
- At 150, [math]\displaystyle{ B }[/math] fails since it would have accumulated an operating age of 120 by this time. It again has to wait for the crew and is repaired by 190.
- At 170, [math]\displaystyle{ C }[/math] fails. Upon this failure, [math]\displaystyle{ C }[/math] requests the only available crew. However, this crew is currently engaged by [math]\displaystyle{ B }[/math] and, since the crew can only perform one task at a time, it cannot respond immediately to the request by [math]\displaystyle{ C }[/math] . Thus, [math]\displaystyle{ C }[/math] will remain failed until the crew becomes available. The crew will finish with unit [math]\displaystyle{ B }[/math] at 190 and will then be dispatched to [math]\displaystyle{ C }[/math] . Upon dispatch, the logistic delay will again be considered and [math]\displaystyle{ C }[/math] will be repaired by 230. The system continues to operate until the failures of [math]\displaystyle{ B }[/math] and [math]\displaystyle{ C }[/math] overlap (i.e. the system is down from 170 to 190)
- At 210, [math]\displaystyle{ D }[/math] fails. It again has to wait for the crew and repair.
- [math]\displaystyle{ D }[/math] is up at 260.
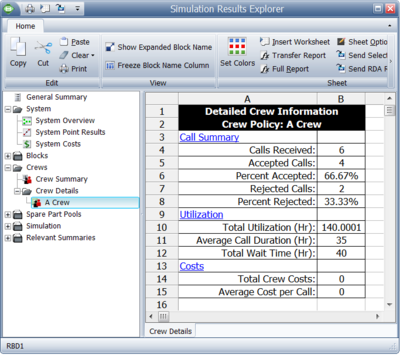
Figure figcrewresults shows an example of some of the possible crew results (details), which are presented next.
Explanation of the Crew Details
- Each request made to a crew is logged.
- If a request is successful (i.e. the crew is available), the call is logged once in the Calls Received counter and once in the Accepted Calls counter.
- If a request is not accepted (i.e. the crew is busy), the call is logged once in the Calls Received counter and once in the Rejected Calls counter. When the crew is free and can be called upon again, the call is logged once in the Calls Received counter and once in the Accepted Calls counter.
- In this scenario, there were two instances when the crew was not available, Rejected Calls = 2, and there were four instances when the crew performed an action, Calls Accepted = 4, for a total of six calls, Calls Received = 6.
- Percent Accepted and Percent Rejected are the ratios of calls accepted and calls rejected with respect to the total calls received.
- Total Utilization is the total time that the crew was used. It includes both the time required to complete the repair action and the logistic time. In this case, this is 140, or:
- [math]\displaystyle{ \begin{align} {{T}_{{{R}_{A}}}}= & 10,{{T}_{{{L}_{A}}}}=20 \\ {{T}_{{{R}_{B}}}}= & 20,{{T}_{{{L}_{B}}}}=20 \\ {{T}_{{{R}_{C}}}}= & 20,{{T}_{{{L}_{C}}}}=20 \\ {{T}_{{{R}_{D}}}}= & 10,{{T}_{{{L}_{D}}}}=20 \\ {{T}_{U}}= & \left( {{T}_{{{R}_{A}}}}+{{T}_{{{L}_{A}}}} \right)+\left( {{T}_{{{R}_{B}}}}+{{T}_{{{L}_{B}}}} \right) \\ & +\left( {{T}_{{{R}_{C}}}}+{{T}_{{{L}_{C}}}} \right)+\left( {{T}_{{{R}_{D}}}}+{{T}_{{{L}_{D}}}} \right) \\ {{T}_{U}}= & 140 \end{align} }[/math]
- 6. Average Call Duration is the average duration of each crew usage, and it also includes both logistic and repair time. It is the total usage divided by the number of accepted calls. In this case, this is 35.
- 7. Total Wait Time is the time that blocks in need of a repair waited for this crew. In this case, it is 40 ( [math]\displaystyle{ C }[/math] and [math]\displaystyle{ D }[/math] both waited 20 each).
- 8. Total Crew Costs are the total costs for this crew. It includes the per incident charge as well as the per unit time costs. In this case, this is 180. There were four incidents at 10 each for a total of 40, as well as 140 time units of usage at 1 cost unit per time unit.
- 9. Average Cost per Call is the total cost divided by the number of accepted calls. In this case, this is 45.
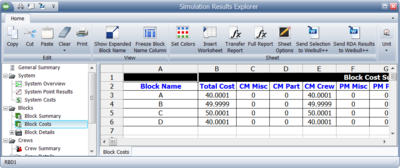
Note that crew costs that are attributed to individual blocks can be obtained from the Blocks reports, as shown in Figure Crewcosts.
How BlockSim Handles Crews
- Crew logistic time is added to each repair time.
- The logistic time is always present, and the same, regardless of where the crew was called from (i.e. whether the crew was at another job or idle at the time of the request).
- For any given simulation, each crew's logistic time is constant (taken from the distribution) across that single simulation run regardless of the task (CM, PM or inspection).
- A crew can perform either a finite number of simultaneous tasks or an infinite number.
- If the finite limit of tasks is reached, the crew will not respond to any additional request until the number of tasks the crew is performing is less than its finite limit.
- If a crew is not available to respond, the component will ``wait until a crew becomes available.
- BlockSim maintains the queue of rejected calls and will dispatch the crew to the next repair on a ``first come, first served basis.
- Multiple crews can be assigned to a single block (see overview in the next section).
- If no crew has been assigned for a block, it is assumed that no crew restrictions exist and a default crew is used. The default crew can perform an infinite number of simultaneous tasks and has no delays or costs.
Looking at Multiple Crews
Multiple crews may be available to perform maintenance for a particular component. When multiple crews have been assigned to a block in BlockSim, the crews are assigned to perform maintenance based on their order in the crew list, as shown in Figure multcrews.
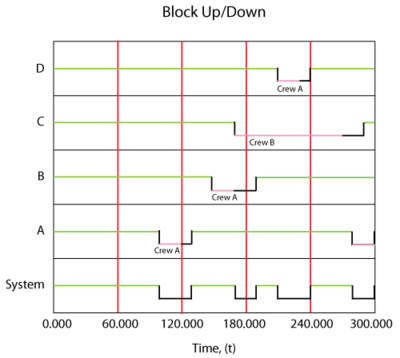
In the case where more than one crew is assigned to a block, and if the first crew is unavailable, then the next crew is called upon and so forth. As an example, consider the prior case but with the following modifications (i.e. Crews [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are assigned to all blocks):
Unit Failure Repair Crew [math]\displaystyle{ A }[/math] [math]\displaystyle{ 100 }[/math] [math]\displaystyle{ 10 }[/math] [math]\displaystyle{ A,B }[/math]
[math]\displaystyle{ B }[/math] [math]\displaystyle{ 120 }[/math] [math]\displaystyle{ 20 }[/math] [math]\displaystyle{ A,B }[/math]
[math]\displaystyle{ C }[/math] [math]\displaystyle{ 140 }[/math] [math]\displaystyle{ 20 }[/math] [math]\displaystyle{ A,B }[/math]
[math]\displaystyle{ D }[/math] [math]\displaystyle{ 160 }[/math] [math]\displaystyle{ 10 }[/math] [math]\displaystyle{ A,B }[/math]
Crew [math]\displaystyle{ A }[/math] ; Delay = 20, Single Task
Crew [math]\displaystyle{ B }[/math] ; Delay = 30, Single Task
The system would behave as shown in Figure figupdown2crew.
In this case, Crew [math]\displaystyle{ B }[/math] was used for the [math]\displaystyle{ C }[/math] repair since Crew [math]\displaystyle{ A }[/math] was busy. On all others, Crew [math]\displaystyle{ A }[/math] was used. It is very important to note that once a crew has been assigned to a task it will complete the task. For example, if we were to change the delay time for Crew [math]\displaystyle{ B }[/math] to 100, the system behavior would be as shown in Figure figupdown2crewalt.
In other words, even though Crew [math]\displaystyle{ A }[/math] would have finished the repair on [math]\displaystyle{ C }[/math] more quickly if it had been available when originally called, [math]\displaystyle{ B }[/math] was assigned the task because [math]\displaystyle{ A }[/math] was not available at the instant that the crew was needed.
Additional Rules on Crews
- 1. If all assigned crews are engaged, the next crew that will be chosen is the crew that can get there first.
- a) This accounts for the time it would take a particular crew to complete its current task (or all tasks in its queue) and its logistic time.
- 2. If a crew is available, it gets used regardless of what its logistic delay time is.
- a) In other words, if a crew with a shorter logistic time is busy, but almost done, and another crew with a much higher logistic time is currently free, the free one will get assigned to the task.
- 3. For each simulation each crew's logistic time is computed (taken randomly from its distribution or its fixed time) at the beginning of the simulation and remains constant across that one simulation for all actions (CM, PM and inspection).
- 1. If all assigned crews are engaged, the next crew that will be chosen is the crew that can get there first.
Using Spare Part Pools
BlockSim also allows you to specify spare part pools (or depots). Spare part pools allow you to model and manage spare part inventory and study the effects associated with limited inventories. Each component can have a spare part pool associated with it. If a spare part pool has not been defined for a block, BlockSim's analysis assumes a default pool of infinite spare parts. To speed up the simulation, no details on pool actions are kept during the simulation if the default pool is used.
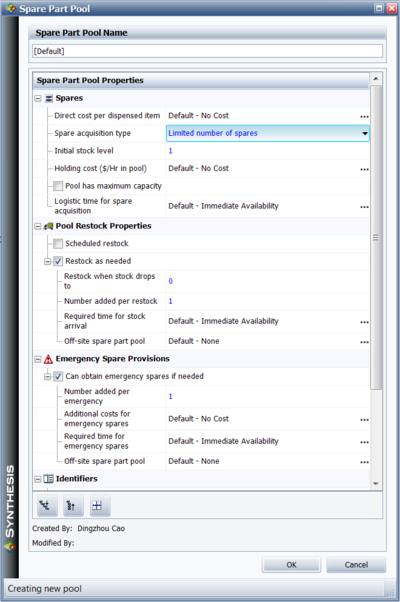
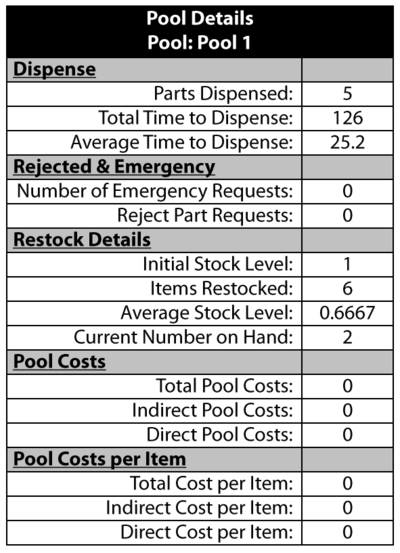
Pools allow you to define multiple aspects of the spare part process, including stock levels, logistic delays and restock options. Every time a part is repaired under a CM or PM action, a spare part is obtained from the pool. If a part is available in the pool, it is then used for the repair. Figures spare1, sparerestock and spareemergency show the pages in BlockSim's Spare Part Pool Properties window. Spare part pools perform their actions based on the simulation clock time.
Spare Properties
A spare part pool is identified by a name. The general properties of the pool are its stock level (must be greater than zero), cost properties and logistic delay time. If a part is available (in stock), the pool will dispense that part to the requesting block after the specified logistic time has elapsed. One needs to think of a pool as an independent entity. It accepts requests for parts from blocks and dispenses them to the requesting blocks after a given logistic time. Requests for spares are handled on a first come, first served basis. In other words, if two blocks request a part and only one part is in stock, the first block that made the request will receive the part. Blocks request parts from the pool immediately upon the initiation of a CM or PM event.
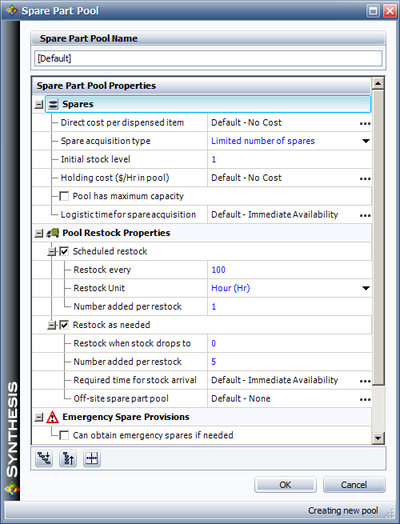
Restocking the Pool
If the pool has a finite number of spares, restock actions may be incorporated. Figure sparerestock shows the restock properties. Specifically, a pool can restock itself either through a scheduled restock action or based on specified conditions.
A scheduled restock action adds a set number of parts to the pool on a predefined scheduled part arrival time. For the settings in Figure sparerestock, one spare part would be added to the pool every 100 time units, based on the system (simulation) time. In other words, for a simulation of 1000 time units, a spare part would arrive at 100 [math]\displaystyle{ tu }[/math] , 200 [math]\displaystyle{ tu }[/math] , etc. The part is available to the pool immediately after the restock action and without any logistic delays.
In an on-condition restock, a restock action is initiated when the stock level reaches (or is below) a specified value. In Figure sparerestock, five parts are ordered when the stock level reaches 0. Note that unlike the scheduled restock, parts added through on-condition restock become available after a specified logistic delay time. In other words, when doing a scheduled restock, the parts are pre-ordered and arrive when needed. Whereas in the on-condition restock, the parts are ordered when the condition occurs and thus arrive after a specified time. For on-condition restocks, the condition is triggered if and only if the stock level drops to or below the specified stock level, regardless of how the spares arrived to the pool or were distributed by the pool. In addition, the restock trigger value must be less than the initial stock.
Lastly, a maximum capacity can be assigned to the pool. If the maximum capacity is reached, no more restock actions are performed. This maximum capacity must be equal to or greater than the initial stock. When this limit is reached, no more items are added to the pool. For example, if the pool has a maximum capacity of ten and a current stock level of eight and if a restock action is set to add five items to the pool, then only two will be accepted.
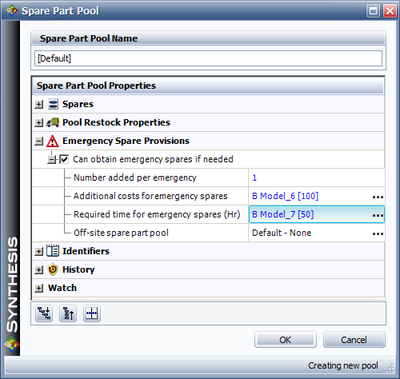
Obtaining Emergency Spares
Emergency restock actions can also be defined. Figure spareemergency illustrates BlockSim's Emergency Spare Provisions options. An emergency action is triggered only when a block requests a spare and the part is not currently in stock. This is the only trigger condition. It does not account for whether a part has been ordered or if one is scheduled to arrive. Emergency spares are ordered when the condition is triggered and arrive after a time equal to the required time to obtain emergency spare(s).
Summary of Rules for Spare Part Pools
The following rules summarize some of the logic when dealing with spare part pools.
Basic Logic Rules
- 1. Queue Based: Requests for spare parts from blocks are queued and executed on a "first come, first served" basis.
- 2. Emergency: Emergency restock actions are performed only when a part is not available.
- 3. Scheduled Restocks: Scheduled restocks are added instantaneously to the pool at the scheduled time.
- 4. On-Condition Restock: On-condition restock happens when the specified condition is reached (e.g. when the stock drops to two or if a request is received for a part and the stock is below the restock level).
- a) For example, if a pool has three items in stock and it dispenses one, an on-condition restock is initiated the instant that the request is received (without regard to the logistic delay time). The restocked items will be available after the required time for stock arrival has elapsed.
- b) The way that this is defined allows for the possibility of multiple restocks. Specifically, every time a part needs to be dispensed and the stock is lower than the specified quantity, parts are ordered. In the case of a long logistic delay time, it is possible to have multiple re-orders in the queue.
- 5. Parts Become Available after Spare Acquisition Logistic Delay: If there is a spare acquisition logistic time delay, the requesting block will get the part after that delay.
- a) For example, if a block with a repair duration of 10 fails at 100 and requests a part from a pool with a logistic delay time of 10, that block will not be up until 120.
- 6. Compound Delays: If a part is not available and an emergency part (or another part) can be obtained, then the total wait time for the part is the sum of both the logistic time and the required time to obtain a spare.
- 7. First Available Part is Dispensed to the First Block in the Queue: The pool will dispense a requested part if it has one in stock or when it becomes available, regardless of what action (i.e. as needed restock or emergency restock) that request may have initiated.
- a) For example, if Block A requests a part from a pool and that triggers an emergency restock action, but a part arrives before the emergency restock through another action (e.g. scheduled restock), then the pool will dispense the newly arrived part to Block A (if Block A is next in the queue to receive a part).
- 8. Blocks that Trigger an Action Get Charged with the Action: A block that triggers an emergency restock is charged for the additional cost to obtain the emergency part, even if it does not use an emergency part (i.e. even if another part becomes available first).
- 9. Triggered Action Cannot be Canceled. If a block triggers a restock action but then receives a part from another source, the action that the block triggered is not canceled.
- a) For example, if Block A initiates an emergency restock action but was then able to use a part that became available through other actions, the emergency request is not canceled and an emergency spare part will be added to the pool's stock level.
- b) Another way to explain this is by looking at the part acquisition logistic times as transit times. Because an ordered part is en-route to you after you order it, you will receive it regardless of whether the conditions have changed and you no longer need it.
Simultaneous Dispatch of Crews and Parts Logic
Some special rules apply when a block has both logistic delays in acquiring parts from a pool and when waiting for crews. BlockSim dispatches requests for crews and spare parts simultaneously. The repair action does not start until both crew and part arrive, as shown next.
If a crew arrives and it has to wait for a part, then this time (and cost) is added to the crew usage time.
Example Using Both Crews and Pools
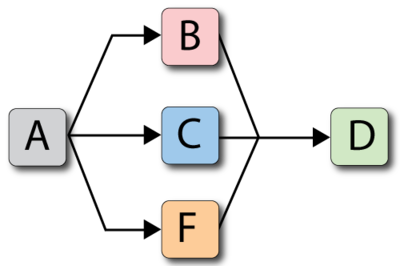
Consider the following example, using both crews and pools.
- Where:
And the crews are:
While the spare pool is:
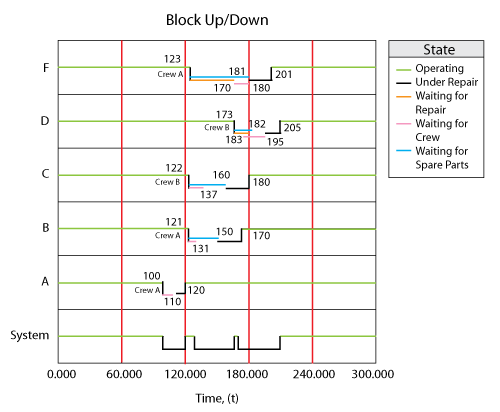
The behavior of this system from 0 to 300 is shown graphically in Figure crew pool.
The discrete system events during that time are as follows:
- 1. Component [math]\displaystyle{ A }[/math] fails at 100 and Crew [math]\displaystyle{ A }[/math] is engaged.
- a) At 110, Crew [math]\displaystyle{ A }[/math] arrives and completes the repair by 120.
- b) This repair uses the only spare part in inventory and triggers an on-condition restock. A part is ordered and is scheduled to arrive at 160.
- c) A scheduled restock part is also set to arrive at 150.
- d) Pool [on-hand = 0, pending: 150, 160].
- 2. Component [math]\displaystyle{ B }[/math] fails at 121. Crew [math]\displaystyle{ A }[/math] is available and it is engaged.
- a) Crew [math]\displaystyle{ A }[/math] arrives by 131 but no part is available.
- b) The failure finds the pool with no parts, triggering the on-condition restock. A part was ordered and is scheduled to arrive at 181.
- c) Pool [on-hand = 0, pending: 150, 160, 181].
- d) At 150, the first part arrives and is used by Component [math]\displaystyle{ B }[/math] .
- e) Repair on Component [math]\displaystyle{ B }[/math] is completed 20 time units later, at 170.
- f) Pool [on-hand=0, pending: 160, 181].
- 3. Component [math]\displaystyle{ C }[/math] fails at 122. Crew [math]\displaystyle{ A }[/math] is already engaged by Component [math]\displaystyle{ B }[/math] , thus Crew [math]\displaystyle{ B }[/math] is engaged.
- a) Crew [math]\displaystyle{ B }[/math] arrives at 137 but no part is available.
- b) The failure finds the pool with no parts, triggering the on-condition restock. A part is ordered and is scheduled to arrive at 182.
- c) Pool [on-hand = 0, pending: 160, 181,182].
- d) At 160, the part arrives and Component [math]\displaystyle{ C }[/math] is repaired by 180.
- e) Pool [on-hand = 0, pending: 181,182].
- 4. Component [math]\displaystyle{ F }[/math] fails at 123. No crews are available until 170 when Crew [math]\displaystyle{ A }[/math] becomes available.
- a) Crew [math]\displaystyle{ A }[/math] arrives by 180 and has to wait for a part.
- b) The failure found the pool with no parts, triggering the on-condition restock. A part is ordered and is scheduled to arrive at 183.
- c) Pool [on-hand = 0, pending: 181,182, 183].
- d) At 181, a part is obtained.
- e) By 201, the repair is completed.
- f) Pool [on-hand = 0, pending: 182, 183]
- 5. Component [math]\displaystyle{ D }[/math] fails at 171 with no crew available.
- a) Crew [math]\displaystyle{ B }[/math] becomes available at 180 and arrives by 195.
- b) The failure finds the pool with no parts, triggering the on-condition restock. A part is ordered and is scheduled to arrive at 231.
- c) The next part becomes available at 182 and the repair is completed by 205.
- d) Pool [on-hand = 0, pending: 183, 231]
- 6. End time is at 300. The last scheduled part arrives at the pool at 300.
Using Maintenance Policies
One of the most important benefits of simulation is the ability to define how and when actions are performed. In our case, the actions of interest are part repairs/replacements. This is accomplished in BlockSim through the use of maintenance policies. Specifically, three different types of policies can be defined for maintenance actions: corrective maintenance, preventive maintenance and inspection.
Corrective Maintenance Policies
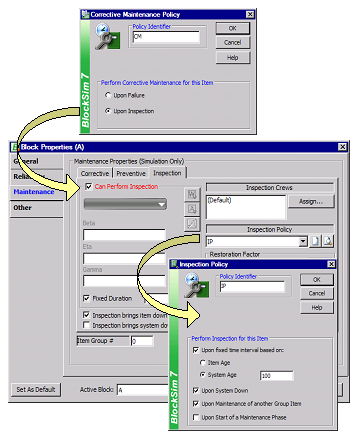
A corrective maintenance policy defines when a corrective maintenance (CM) action is performed. Figure CorrPolicy shows a corrective maintenance policy assigned to a block in BlockSim.
Corrective actions will be performed either immediately upon failure of the item or upon finding that the item has failed (for hidden failures that are not detected until an inspection). BlockSim allows the selection of either category. If Upon Failure is selected, the CM action is initiated immediately upon failure. If no policy has been set for a block, then this is the default option. All prior examples were based on the instruction to perform a CM upon failure. If the Upon Inspection option is selected, then the CM action will only be initiated after an inspection is done on the failed component. How and when the inspections are performed is defined by the block's inspection properties and also by the inspection policy. This has the effect of defining a dependency between the corrective maintenance policy and the inspection policy, as shown in Figure uponInspection.
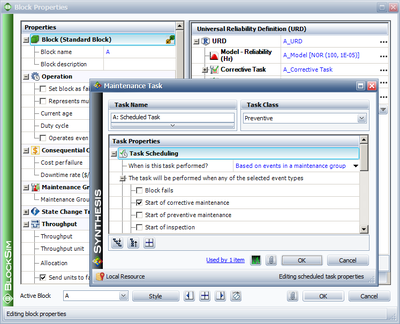
Inspection Policies
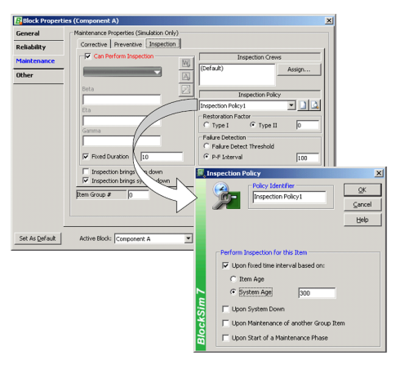
Figure uponInspection shows the options available in an inspection policy within BlockSim. Inspections can be performed upon a fixed time interval. This is either based on the item's age (item clock) or the system's age (system clock). Furthermore, inspections can also be set to occur if the system goes down or if another group item goes down. Within BlockSim, items are considered to be in the same group if they have the same non-zero Item Group #. Note that the default value for this is 0. Zero is a reserved number and it means that the item does not belong to any group. Inspections do not bring the item down by default.
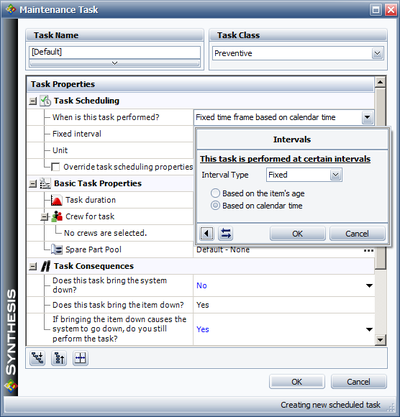
Preventive Maintenance Policies
Figure PMPolicy shows the options available in a preventive maintenance (PM) policy within BlockSim. Much like inspections, PMs can be performed upon a fixed time interval. This is either based on the item's age (item clock) or the system's age (system clock). Furthermore, PM actions can also be set to occur if the system goes down or if another group item goes down. Because PM actions always bring the item down, one can also specify whether preventive maintenance will be performed if the action brings the system down.
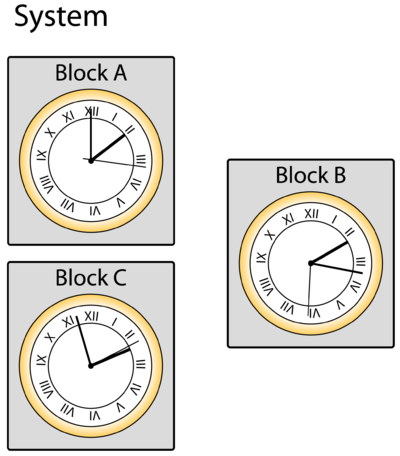
Item and System Ages
It is important to keep in mind that the system and each component of the system maintains a separate clock within the simulation. Figure clocks illustrates system and item clocks. The system clock is the simulation elapsed time while the item clock is the age of the item since last renewal. If the system clock is used, the inspection will be performed every [math]\displaystyle{ X }[/math] time units. If the item clock is used, the inspection will be performed every time the component reaches that age. As an example, if the inspection is set to be performed at a system age of 100, then an inspection will be performed at 100, 200, 300 and so forth. If the inspection is set based on an item's age of 100, then the inspection will be performed when the item reaches an age of 100.
Failure Detection
Inspection tasks can be used to check for indications of an approaching failure. BlockSim models such indications of when an approaching failure will become detectable upon inspection using Failure Detection Threshold and P-F Interval. Failure detection threshold allows the user to enter a number between 0 and 1 indicating the percentage of an item's life that must elapse before an approaching failure can be detected. For instance, if the failure detection threshold value is set as 0.8 then this means that the failure of a component can be detected only during the last 20% of its life. If an inspection occurs during this time, an approaching failure is detected and the inspection triggers a preventive maintenance task to take the necessary precautions to delay the failure by either repairing or replacing the component.
The P-F interval allows the user to enter the amount of time before the failure of a component when the approaching failure can be detected by an inspection. The P-F interval represents the warning period that spans from P(when a potential failure can be detected) to F(when the failure occurs). If a P-F interval is set as 200 then the approaching failure of the component can only be detected 200 time units (tu) before the failure of the component. Thus, if a component has a fixed life of 1,000 tu and the P-F interval is set to 200 tu, then if an inspection occurs at or beyond 800 tu, the approaching failure of the component that is to occur at 1,000 tu is detected by this inspection and a preventive maintenance task is triggered to take action against this failure.
Example using P-F Interval
To illustrate the use of the P-F interval in BlockSim, consider a component [math]\displaystyle{ A }[/math] that fails every 700 tu. The corrective maintenance on this equipment takes 100 tu to complete, while the preventive maintenance takes 50 tu to complete. Both the corrective and preventive maintenance actions have a type II restoration factor of 1. Inspection tasks of 10 tu duration are performed on the component every 300 tu. There is no restoration of the component during the inspections. The P-F interval for this component is 100 tu (see Figure InsPolPFinterval).
Component Overview
The component behavior from 0 to 2000 tu is shown in Figure PFinterval and described next.
- At 300 tu the first scheduled inspection of 10 tu duration occurs. At this time the age of the component is 300 tu. This inspection does not lie in the P-F interval of 100 tu (which begins at the age of 600 tu and ends at the age of 700 tu). Thus, no approaching failure is detected during this inspection.
- At 600 tu the second scheduled inspection of 10 tu duration occurs. At this time the age of the component is 590 tu (no age is accumulated during the first inspection from 300 tu to 310 tu as the component does not operate during this inspection). Again this inspection does not lie in the P-F interval. Thus, no approaching failure is detected during this inspection.
- At 720 tu the component fails after having accumulated an age of 700 tu. A corrective maintenance task of 100 tu duration occurs to restore the component to as-good-as-new condition.
- At 900 tu the third scheduled inspection occurs. At this time the age of the component is 80 tu. This inspection does not lie in the P-F interval (from age 600 tu to 700 tu). Thus, no approaching failure is detected during this inspection.
- At 1200 tu the fourth scheduled inspection occurs. At this time the age of the component is 370 tu. Again, this inspection does not lie in the P-F interval and no approaching failure is detected.
- At 1500 tu the fifth scheduled inspection occurs. At this time the age of the component is 660 tu, which lies in the P-F interval. As a result, an approaching failure is detected and the inspection triggers a preventive maintenance task. A preventive maintenance task of 50 tu duration occurs at 1510 tu to restore the component to as-good-as-new condition.
- At 1800 tu the sixth scheduled inspection occurs. At this time the age of the component is 240 tu. This inspection does not lie in the P-F interval (from age 600 tu to 700 tu) and no approaching failure is detected.
Rules for PMs and Inspections
All the options available in the Maintenance tab of the Block Properties window and the associated policies were designed to maximize the modeling flexibility within BlockSim. However, maximizing the modeling flexibility introduces issues that you need to be aware of and requires you to carefully select options in order to assure that the selections do not contradict one another. One obvious case would be to define a PM action on a component in series (which will always bring the system down) and then assign a PM policy to the block that has the Do not perform maintenance if the action brings the system down option set. With these settings, no PMs will ever be performed on the component during the BlockSim simulation. The following sections summarize some issues and special cases to consider when defining maintenance properties and policies in BlockSim.
- Inspections do not consume spare parts. However, an inspection can have a renewal effect on the component if the restoration factor is set to a number other than the default of 0.
- On the inspection tab, if Inspection brings system down is selected, this also implies that the inspection brings the item down.
- If a PM or an inspection are scheduled based on the item's age, then they will occur exactly when the item reaches that age. However, it is important to note that failed items do not age. Thus, if an item fails before it reaches that age, the action will not be performed. This means that if the item fails before the scheduled inspection (based on item age) and the CM is set to be performed upon inspection, the CM will never take place. The reason that this option is allowed in BlockSim is for the flexibility of specifying renewing inspections.
- Downtime due to a failure discovered during a non-downing inspection is included when computing results ``w/o PM & Inspections.
- If a PM upon item age is scheduled and is not performed because it brings the system down (based on the option in the PM policy) the PM will not happen unless the item reaches that age again (after restoration by CM, inspection or another type of PM).
- If the CM policy is upon inspection and a failed component is scheduled for PM prior to the inspection, the PM action will restore the component and the CM will not take place.
- In the case of simultaneous events, only one event is executed. The following precedence order is used: inspection, preventive maintenance, corrective maintenance.
- The PM option of Do not perform if it brings the system down is only considered at the time that the PM needs to be initiated. If the system is down at that time, due to another item, then the PM will be performed regardless of any future consequences to the system up state. In other words, when the other item is fixed, it is possible that the system will remain down due to this PM action. In this case, the PM time difference is added to the system PM downtime.
- If the CM policy is upon inspection, the inspection does not restore the block, only the CM restores the block.
- Downing events cannot overlap. If a component is down due to a PM and another PM is suggested based on another trigger, the second call is ignored.
- A non-downing inspection with a restoration factor restores the block based on the age of the block at the beginning of the inspection (i.e. duration is not restored). Note that this is different from BlockSim 6.
- Non-downing events can overlap with downing events. If in a non-downing inspection and a downing event happen concurrently, the non-downing event will be managed in parallel with the downing event.
- If a failure or PM occurs during a non-downing inspection and the CM or PM has a restoration factor and the inspection action has a restoration factor, then both restoration factors are used (compounded).
- A PM or inspection on system down is triggered only if the system was up at the time that the event brought the system down.
- A non-downing inspection with restoration factor of 0 does not affect the block.
- An inspection that finds a block at or beyond the failure detect threshold will trigger a preventive maintenance action as long as preventive maintenance can be performed on that block.
- An inspection that finds a block within the range of the P-F Interval will trigger a preventive maintenance action as long as preventive maintenance can be performed on that block.
Example
To illustrate the use of maintenance policies in BlockSim we will use the same example from Section 8.example with the following modifications (Figures exPMpolicy and exinspection also show these settings):
Blocks A and D:
- Belong to the same group (Group 1).
- Corrective maintenance actions are upon inspection (not upon failure) and the inspections are performed every 30 [math]\displaystyle{ tu }[/math] based on system time. Inspections have a duration of 1 [math]\displaystyle{ tu }[/math] . Furthermore, unlimited free crews are available to perform the inspections.
- Whenever either item fails, the other one gets a PM.
- The PM has a fixed duration of 10 [math]\displaystyle{ tu }[/math] .
- The same crews are used for both corrective and preventive maintenance actions.
System Overview
The item and system behavior from 0 to 300 hours is shown in Figure eventex2 and described next.
- 1. At 100, block [math]\displaystyle{ A }[/math] goes down and brings the system down.
- a) No maintenance action is performed since an upon inspection policy was used.
- b) The next scheduled inspection is at 120, thus Crew [math]\displaystyle{ A }[/math] is called to perform the maintenance by 121 (end of the inspection).
- 2. Crew [math]\displaystyle{ A }[/math] arrives and initiates the repair on [math]\displaystyle{ A }[/math] at 131.
- a) The only part in the pool is used and an on-condition restock is triggered.
- b) Pool [on-hand = 0, pending: 150 [math]\displaystyle{ _{s} }[/math] , 181].
- c) Block [math]\displaystyle{ A }[/math] is repaired by 141.
- 3. At the same time (121), a PM is initiated for block [math]\displaystyle{ D }[/math] because the PM policy called for ``PM upon a maintenance action on another group item.
- a) Crew [math]\displaystyle{ B }[/math] is called for block [math]\displaystyle{ D }[/math] and arrives at 136.
- b) No part is available until 150. An on-condition restock is triggered for 181.
- c) Pool [on-hand = 0, pending: 150 [math]\displaystyle{ _{s} }[/math] , 181, 181].
- d) At 150, a part becomes available and the PM is completed by 160.
- e) Pool [on-hand = 0, pending: 181, 181].
- 4. At 161, block [math]\displaystyle{ B }[/math] fails (corrective maintenance upon failure).
- a) Block [math]\displaystyle{ B }[/math] gets Crew [math]\displaystyle{ A }[/math] , which arrives at 171.
- b) No part is available until 181. An on-condition restock is triggered for 221.
- c) Pool [on-hand = 0, pending: 181, 181, 221].
- d) A part arrives at 181.
- e) The repair is completed by 201.
- f) Pool [on-hand = 0, pending: 181, 221].
- 5. At 162, block [math]\displaystyle{ C }[/math] fails.
- a) Block [math]\displaystyle{ C }[/math] gets Crew [math]\displaystyle{ B }[/math] , which arrives at 177.
- b) No part is available until 181. An on-condition restock is triggered for 222.
- c) Pool [on-hand = 0, pending: 181, 221, 222].
- d) A part arrives at 181.
- e) The repair is completed by 201.
- f) Pool [on-hand = 0, pending: 221, 222].
- 6. At 163, block [math]\displaystyle{ F }[/math] fails and brings the system down.
- a) Block [math]\displaystyle{ F }[/math] calls Crew [math]\displaystyle{ A }[/math] then [math]\displaystyle{ B }[/math] . Both are busy.
- b) Crew [math]\displaystyle{ A }[/math] will be the first available so .. calls [math]\displaystyle{ A }[/math] again and waits.
- c) No part is available until 221. An on-condition restock is triggered for 223.
- d) Pool [on-hand = 0, pending: 221, 222, 223].
- e) Crew [math]\displaystyle{ A }[/math] arrives at 211.
- f) Repair begins at 221.
- g) Repair is completed by 241.
- h) Pool [on-hand = 0, pending: 222, 223].
- 7. At 298, block [math]\displaystyle{ A }[/math] goes down and brings the system down.
- 1. At 100, block [math]\displaystyle{ A }[/math] goes down and brings the system down.
System Uptimes/Downtimes
- 1. System Uptime: This is 200 [math]\displaystyle{ tu }[/math] .
- a) This can be obtained by observing the following system up durations: 0 to 100, 160 to 163 and 201 to 298.
- 2. System CM Downtime: This is 58 [math]\displaystyle{ tu }[/math] .
- a) Observe that even though the system failed at 100, the CM action (on block [math]\displaystyle{ A }[/math] ) was initiated at 121 and lasted until 141, thus only 20 [math]\displaystyle{ tu }[/math] of this downtime are attributed to the CM action.
- b) The next CM action started at 163 when block [math]\displaystyle{ F }[/math] failed and lasted until 201 when blocks [math]\displaystyle{ B }[/math] and [math]\displaystyle{ C }[/math] were restored, thus adding another 38 [math]\displaystyle{ tu }[/math] of CM downtime.
- 3. System Inspection Downtime: This is 1 [math]\displaystyle{ tu. }[/math]
- a) The only time the system was under inspection was from 120 to 121, during the inspection of block [math]\displaystyle{ A }[/math] .
- 1. System Uptime: This is 200 [math]\displaystyle{ tu }[/math] .
- 4. System PM Downtime: This is 19 [math]\displaystyle{ tu }[/math] .
- a) Note that the entire PM action duration on block [math]\displaystyle{ D }[/math] was from 121 to 160.
- b) Until 141, and from the system perspective, the CM on block [math]\displaystyle{ A }[/math] was the cause for the downing. Once block [math]\displaystyle{ A }[/math] was restored (at 141), then the reason for the system being down became the PM on block [math]\displaystyle{ D }[/math] .
- c) Thus, the PM on block [math]\displaystyle{ D }[/math] was only responsible for the downtime after block [math]\displaystyle{ A }[/math] was restored, or from 141 to 160.
- 5. System Total Downtime: This is 100 [math]\displaystyle{ tu. }[/math]
- a) This includes all of the above downtimes plus the 20 [math]\displaystyle{ tu }[/math] (100 to 120) and the 2 [math]\displaystyle{ tu }[/math] (298 to 300) that the system was down due the undiscovered failure of block [math]\displaystyle{ A }[/math] .
- 4. System PM Downtime: This is 19 [math]\displaystyle{ tu }[/math] .
System Metrics
- 1. Mean Availability (All Events):
- [math]\displaystyle{ \frac{300-100}{300}=0.6667 }[/math]
- 2. Mean Availability (w/o PM & Inspection):
- a) This is due to the CM downtime of 58, the undiscovered downtime of 22 and the inspection downtime of 1, or:
- [math]\displaystyle{ \frac{300-(58+22+1)}{300}=0.7333 }[/math]
- b) It should be noted that the inspection downtime was included even though the definition was ``w/o PM & Inspection. The reason for this is that the inspection did not cause the downtime in this case. Only downtimes caused by the PM or inspections are excluded.
- 3. Point Availability and Reliability at 300 is zero because the system was down at 300.
- 4. Expected Number of Failures is 3.
- a) The system failed at 100, 163 and 298.
- 5. The MTTFF is 100 because the example is deterministic.
The System Downing Events
- 1. Number of Failures is 3.
- a) The first is the failure of block [math]\displaystyle{ A }[/math] , the second is the failure of block [math]\displaystyle{ F }[/math] and the third is the failure of block [math]\displaystyle{ A }[/math] .
- 2. Number of CMs is 2.
- a) The first is the CM on block [math]\displaystyle{ A }[/math] and the second is the CM on block [math]\displaystyle{ F }[/math] .
- 3. Number of Inspections is 1.
- 4. Number of PMs is 1.
- 5. Total Events are 6. These are events that the downtime can be attributed to. Specifically, the following events were observed:
- a) The failure of block [math]\displaystyle{ A }[/math] at 100.
- b) Inspection on block [math]\displaystyle{ A }[/math] at 120.
- c) The CM action on block [math]\displaystyle{ A }[/math] .
- d) The PM action on block [math]\displaystyle{ D }[/math] (after [math]\displaystyle{ A }[/math] was fixed).
- e) The failure of block [math]\displaystyle{ F }[/math] at 163.
- f) The failure of block .. at 298.
- 1. Number of Failures is 3.
Block Details
The details for blocks [math]\displaystyle{ A,B,C,D }[/math] and [math]\displaystyle{ F }[/math] are shown in Figure FigTable.
We will discuss some of these results. First note that there are four downing events on block [math]\displaystyle{ A }[/math] : initial failure, inspection and CM, plus the last failure at 298. All others have just one. Also, block [math]\displaystyle{ A }[/math] had a total downtime of [math]\displaystyle{ 41+2 }[/math] , giving it a mean availability of 0.8567. The first time-to-failure for block [math]\displaystyle{ A }[/math] occurred at 100 while the second occurred after [math]\displaystyle{ 298-141=157 }[/math] hours of operation, yielding an average time between failures (MTBF) of [math]\displaystyle{ 257/2=128.5 }[/math] . (Note that this is the same as uptime/failures.) Block [math]\displaystyle{ D }[/math] never failed, so its MTBF cannot be determined. Furthermore, MTBDE for each item is determined by dividing the block's uptime by the number of events. The RS FCI and RS DECI metrics are obtained by looking at the SD Failures and SD Events of the item and the number of system failures and events. Specifically, the only items that caused system failure are blocks [math]\displaystyle{ A }[/math] and [math]\displaystyle{ F }[/math] ; [math]\displaystyle{ A }[/math] at 100 and 298 and [math]\displaystyle{ F }[/math] at 163. It is important to note that even though one could argue that block [math]\displaystyle{ F }[/math] alone did not cause the failure ( [math]\displaystyle{ B }[/math] and [math]\displaystyle{ C }[/math] were also failed), the downing was attributed to [math]\displaystyle{ F }[/math] because the system reached a failed state only when block [math]\displaystyle{ F }[/math] failed.
On the number of inspections, which were scheduled every 30 [math]\displaystyle{ tu, }[/math] nine occurred for block [math]\displaystyle{ A }[/math] [30, 60, 90, 120, 150, 180, 210, 240, 270] and eight for block [math]\displaystyle{ D }[/math] . Block [math]\displaystyle{ D }[/math] did not get inspected at 150 because block [math]\displaystyle{ D }[/math] was undergoing a PM action at that time.
Crew Details
Figure Crew detail shows the crew results. Crew [math]\displaystyle{ A }[/math] received a total of six calls and accepted three. Specifically,
- At 121, the crew was called by block [math]\displaystyle{ A }[/math] and the call was accepted.
- At 121, block [math]\displaystyle{ D }[/math] also called for its PM action and was rejected. Block [math]\displaystyle{ D }[/math] then called crew [math]\displaystyle{ B }[/math] , which accepted the call.
- At 161, block [math]\displaystyle{ B }[/math] called crew [math]\displaystyle{ A }[/math] . Crew [math]\displaystyle{ A }[/math] accepted.
- At 162, block [math]\displaystyle{ C }[/math] called crew [math]\displaystyle{ A }[/math] . Crew [math]\displaystyle{ A }[/math] rejected and block [math]\displaystyle{ C }[/math] called crew [math]\displaystyle{ B }[/math] , which accepted the call.
- At 163, block [math]\displaystyle{ F }[/math] called crew [math]\displaystyle{ A }[/math] and then crew [math]\displaystyle{ B }[/math] and both rejected. Block [math]\displaystyle{ F }[/math] then waited until a crew became available at 201 and called that crew again. This was crew [math]\displaystyle{ A }[/math] , which accepted.
The total wait time is the time that blocks had to wait for the maintenance crew. Block [math]\displaystyle{ F }[/math] is the only component that waited, waiting 38 [math]\displaystyle{ tu }[/math] for crew [math]\displaystyle{ A }[/math] .
Also, the costs for crew [math]\displaystyle{ A }[/math] were 1 per unit time and 10 per incident, thus the total costs were 100 + 30. The costs for Crew [math]\displaystyle{ B }[/math] were 2 per unit time and 20 per incident, thus the total costs were 156 + 40.
Pool Details
Figure poolfig shows the spare part pool results. The pool started with a stock level of 1 and ended up with 2. Specifically,
- At 121, the pool dispensed a part to block [math]\displaystyle{ A }[/math] and ordered another to arrive at 181.
- At 121, it dispensed a part to block [math]\displaystyle{ D }[/math] and ordered another to arrive at 181.
- At 150, a scheduled part arrived to restock the pool.
- At 161 the pool dispensed a part to block [math]\displaystyle{ B }[/math] and ordered another to arrive at 221.
- At 181, it dispensed a part to block [math]\displaystyle{ C }[/math] and ordered another to arrive at 222.
- At 221, it dispensed a part to block [math]\displaystyle{ F }[/math] and ordered another to arrive at 223.
- The 222 and 223 arrivals remained in stock until the end of the simulation.
Overall, five parts were dispensed. Blocks had to wait a total of 126 [math]\displaystyle{ tu }[/math] to receive parts ( [math]\displaystyle{ B\ \ :\ \ 181-161=20 }[/math] , [math]\displaystyle{ C\ \ :\ \ 181-162=19 }[/math] , [math]\displaystyle{ D\ \ :\ \ 150-121=29 }[/math] and [math]\displaystyle{ F\ \ :\ \ 221-163=58 }[/math] ).
Special Cases
To illustrate some special cases that you should be aware of, consider the following diagram.
In this diagram, blocks [math]\displaystyle{ A }[/math] and [math]\displaystyle{ D }[/math] have the same properties as before, with the exception that the inspection duration is now set to zero. Furthermore, recall the rule that only one event is executed in the case of simultaneous events. In this case and when block [math]\displaystyle{ A }[/math] fails, the inspection on block [math]\displaystyle{ A }[/math] at 120 will find the failure of [math]\displaystyle{ A }[/math] , which will then trigger a PM event on block [math]\displaystyle{ D }[/math] at the same instant that [math]\displaystyle{ D }[/math] also gets an inspection. This causes two simultaneous events on block [math]\displaystyle{ D }[/math] . This will result in the cancellation of the PM event on block [math]\displaystyle{ D }[/math] . The reason for the cancellation is to avoid the recursive situation where the PM on [math]\displaystyle{ D }[/math] would trigger a PM on [math]\displaystyle{ A }[/math] , which is undergoing CM, which would trigger a PM on [math]\displaystyle{ D }[/math] and so forth. Different options can be used to avoid this. One is to assign a non-zero inspection duration. In this case, the PM on block [math]\displaystyle{ D }[/math] would get triggered after the inspection on block [math]\displaystyle{ A }[/math] , as seen in the prior example.
Subdiagrams and Multi Blocks in Simulation
Any subdiagrams and multi blocks that may be present in the BlockSim RBD are expanded and/or merged into a single diagram before the system is simulated. As an example, consider the system shown in Figure figSub.
BlockSim will internally merge the system into a single diagram before the simulation, as shown in Figure figsubexpand. This means that all the failure and repair properties of the items in the subdiagrams are also considered.
If a subdiagram represents a line-replaceable item, such as a circuit board that was swapped out during repair, and you do not wish to model the time that it takes to repair/replace components inside the circuit board, then the failure distribution should be obtained for the subdiagram (using the component properties) and individual repair properties should be added at the subdiagram level. Figure figunlink illustrates this option in the BlockSim Block Properties window.
In the case of multi blocks, the blocks are also fully expanded before simulation. This means that unlike the analytical solution, the execution speed (and memory requirements) for a multi block representing ten blocks in series is identical to the representation of ten individual blocks in series.
Containers in Simulation
Standby Containers
In the case of a standby container, the container acts as the switch mechanism (Figure standbycontainer) in addition to defining the standby relationships and the number of active units that are required. The container's failure and repair properties are really that of the switch itself. The switch can fail with a distribution, while waiting to switch or during the switch action. Repair properties restore the switch regardless of how the switch failed. Failure of the switch itself does not bring the container down because the switch is not really needed unless called upon to switch. The container will go down if the units within the container fail or the switch is failed when a switch action is needed. The restoration time for this is based on the repair distributions of the contained units and the switch. Furthermore, the container is down during a switch process that has a delay.
[math]\displaystyle{ }[/math]
To better illustrate this, consider the following deterministic case.
- Units [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are contained in a standby container.
- The standby container is the only item in the diagram, thus failure of the container is the same as failure of the system.
- [math]\displaystyle{ A }[/math] is the active unit and [math]\displaystyle{ B }[/math] is the standby unit.
- Unit [math]\displaystyle{ A }[/math] fails every 100 [math]\displaystyle{ tu }[/math] (active) and takes 10 [math]\displaystyle{ tu }[/math] to repair.
- [math]\displaystyle{ B }[/math] fails every 3 [math]\displaystyle{ tu }[/math] (active) and also takes 10 [math]\displaystyle{ tu }[/math] to repair.
- The units cannot fail while in quiescent (standby) mode.
- Furthermore, assume that the container (acting as the switch) fails every 30 [math]\displaystyle{ tu }[/math] while waiting to switch and takes 4 [math]\displaystyle{ tu }[/math] to repair. If not failed, the container switches with 100% probability.
- The switch action takes 7 [math]\displaystyle{ tu }[/math] to complete.
- After repair, unit [math]\displaystyle{ A }[/math] is always reactivated.
- The container does not operate through system failure and thus the components do not either.
Keep in mind that we are looking at two events on the container. The container down and container switch down.
The system event log is shown in Figure standbyupdown and is as follows:
- At 30, the switch fails and gets repaired by 34. The container switch is failed and being repaired; however, the container is up during this time.
- At 64, the switch fails and gets repaired by 68. The container is up during this time.
- At 98, the switch fails. It will be repaired by 102.
- At 100, unit [math]\displaystyle{ A }[/math] fails. Unit [math]\displaystyle{ A }[/math] attempts to activate the switch to go to [math]\displaystyle{ B }[/math] ; however, the switch is failed.
- At 102, the switch is operational.
- From 102 to 109, the switch is in the process of switching from unit [math]\displaystyle{ A }[/math] to unit [math]\displaystyle{ B }[/math] . The container and system are down from 100 to 109.
- By 110, unit [math]\displaystyle{ A }[/math] is fixed and the system is switched back to [math]\displaystyle{ A }[/math] from [math]\displaystyle{ B }[/math] . The return switch action brings the container down for 7 [math]\displaystyle{ tu }[/math] , from 110 to 117. During this time, note that unit [math]\displaystyle{ B }[/math] has only functioned for 1 [math]\displaystyle{ tu }[/math] , 109 to 110.
- At 146, the switch fails and gets repaired by 150. The container is up during this time.
- At 180, the switch fails and gets repaired by 184. The container is up during this time.
- At 214, the switch fails and gets repaired by 218.
- At 217, unit [math]\displaystyle{ A }[/math] fails. The switch is failed at this time.
- At 218, the switch is operational and the system is switched to unit [math]\displaystyle{ B }[/math] within 7 [math]\displaystyle{ tu }[/math] . The container is down from 218 to 225.
- At 225, unit [math]\displaystyle{ B }[/math] takes over. After 2 [math]\displaystyle{ tu }[/math] of operation at 227, unit [math]\displaystyle{ B }[/math] fails. It will be restored by 237.
- At 227, unit [math]\displaystyle{ A }[/math] is repaired and the switchback action to unit [math]\displaystyle{ A }[/math] is initiated. By 234, the system is up.
- At 262, the switch fails and gets repaired by 266. The container is up during this time.
- At 296, the switch fails and gets repaired by 300. The container is up during this time.
The system results are shown in Figure StandbySysOverview and discussed next.
- 1. System CM Downtime is 24.
- a) CM downtime includes all downtime due to failures as well as the delay in switching from a failed active unit to a standby unit. It does not include the switchback time from the standby to the restored active unit. Thus, the times from 100 to 109, 217 to 225 and 227 to 234 are included. The time to switchback, 110 to 117, is not included.
- 2. System Total Downtime is 31.
- a) It includes the CM downtime and the switchback downtime.
- 3. Number of System Failures is 3.
- a) It includes the failures at 100, 217 and 227.
- b) This is the same as the number of CM downing events.
- 4. The Total Downing Events are 4.
- a) This includes the switchback downing event at 110.
- 5. The Mean Availability (w/o PM and Inspection) does not include the downtime due to the switchback event.
- 1. System CM Downtime is 24.
Additional Rules and Assumptions for Standby Containers
- 1) A container will only attempt to switch if there is an available non-failed item to switch to. If there is no such item, it will then switch if and when an item becomes available. The switch will cancel the action if it gets restored before an item becomes available.
- a) As an example, consider the case of unit [math]\displaystyle{ A }[/math] failing active while unit [math]\displaystyle{ B }[/math] failed in a quiescent mode. If unit [math]\displaystyle{ B }[/math] gets restored before unit [math]\displaystyle{ A }[/math] , then the switch will be initiated. If unit [math]\displaystyle{ A }[/math] is restored before unit [math]\displaystyle{ B }[/math] , the switch action will not occur.
- 2) In cases where not all active units are required, a switch will only occur if the failed combination causes the container to fail.
- a) For example, if [math]\displaystyle{ A }[/math] , [math]\displaystyle{ B }[/math] and [math]\displaystyle{ C }[/math] are in a container for which one unit is required to be operating and [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are active with [math]\displaystyle{ C }[/math] on standby, then the failure of either [math]\displaystyle{ A }[/math] or [math]\displaystyle{ B }[/math] will not cause a switching action. The container will switch to [math]\displaystyle{ C }[/math] only if both [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are failed.
- 3) If the container switch is failed and a switching action is required, the switching action will occur after the switch has been restored if it is still required (i.e. if the active unit is still failed).
- 4) If a switch fails during the delay time of the switching action based on the reliability distribution (quiescent failure mode), the action is still carried out unless a failure based on the switch probability/restarts occurs when attempting to switch.
- 5) During switching events, the change from the operating to quiescent distribution (and vice versa) occurs at the end of the delay time.
- 6) The option of whether components operate while the system is down is defined at the container level. Contained items inherit this property from the container (just as they do in a load sharing container). However, and regardless of the container settings:
- a) If a path inside the container is down, blocks inside the container that are in that path do not continue to operate.
- b) Blocks that are up do not continue to operate while the container is down.
- 7) The duty cycle for a standby container is defined at the container level. Contained items and the switch inherit this property from the container.
- 8) A switch can have a repair distribution and maintenance properties without having a reliability distribution.
- a) This is because maintenance actions are performed regardless of whether the switch failed while waiting to switch (reliability distribution) or during the actual switching process (fixed probability).
- 9) A switch fails during switching when the restarts are exhausted.
- 10) A restart is executed every time the switch fails to switch (based on its fixed probability of switching).
- 11) If a delay is specified, restarts happen after the delay.
- 12) If a container brings the system down, the container is responsible for the system going down (not the blocks inside the container).
- 13) A switch will trigger a corrective maintenance for a standby block that fails in the quiescent mode and has a CM policy of Upon Inspection.
- 1) A container will only attempt to switch if there is an available non-failed item to switch to. If there is no such item, it will then switch if and when an item becomes available. The switch will cancel the action if it gets restored before an item becomes available.
Load Sharing Containers
In the case of a load sharing container, the container defines the load that is shared. A load sharing container has no failure or repair distributions. The container itself is considered failed if all the blocks inside the container have failed (or [math]\displaystyle{ k }[/math] blocks in a [math]\displaystyle{ k }[/math] -out-of- [math]\displaystyle{ n }[/math] configuration).
To illustrate this, consider the following container with items [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] in a load sharing redundancy.
Assume that [math]\displaystyle{ A }[/math] fails every 100 [math]\displaystyle{ tu }[/math] and [math]\displaystyle{ B }[/math] every 120 [math]\displaystyle{ tu }[/math] if both items are operating and they fail in half that time if either is operating alone (i.e. the items age twice as fast when operating alone). They both get repaired in 5 [math]\displaystyle{ tu }[/math] .
The system event log is shown in Figure figloadshare and is as follows:
- 1. At 100, [math]\displaystyle{ A }[/math] fails. It takes 5 [math]\displaystyle{ tu }[/math] to restore [math]\displaystyle{ A }[/math] .
- 2. From 100 to 105, [math]\displaystyle{ B }[/math] is operating alone and is experiencing a higher load.
- 3. At 115, [math]\displaystyle{ B }[/math] fails. would normally be expected to fail at 120, however:
- a) From 0 to 100, it accumulated the equivalent of 100 [math]\displaystyle{ tu }[/math] of damage.
- b) From 100 to 105, it accumulated 10 [math]\displaystyle{ tu }[/math] of damage, which is twice the damage since it was operating alone. Put another way, [math]\displaystyle{ B }[/math] aged by 10 [math]\displaystyle{ tu }[/math] over a period of 5 [math]\displaystyle{ tu }[/math] .
- c) At 105, [math]\displaystyle{ A }[/math] is restored but [math]\displaystyle{ B }[/math] has only 10 [math]\displaystyle{ tu }[/math] of life remaining at this point.
- d) [math]\displaystyle{ B }[/math] fails at 115.
- 4. At 120, [math]\displaystyle{ B }[/math] is repaired.
- 5. At 200, [math]\displaystyle{ A }[/math] fails again. [math]\displaystyle{ A }[/math] would normally be expected to fail at 205; however, the failure of [math]\displaystyle{ B }[/math] at 115 to 120 added additional damage to [math]\displaystyle{ A }[/math] . In other words, the age of [math]\displaystyle{ A }[/math] at 115 was 10; by 120 it was 20. Thus it reached an age of 100 95 [math]\displaystyle{ tu }[/math] later at 200.
- 6. [math]\displaystyle{ A }[/math] is restored by 205.
- 7. At 235, [math]\displaystyle{ B }[/math] fails. [math]\displaystyle{ B }[/math] would normally be expected to fail at 240; however, the failure of [math]\displaystyle{ A }[/math] at 200 caused the reduction.
- a) At 200, [math]\displaystyle{ B }[/math] had an age of 80.
- b) By 205, [math]\displaystyle{ B }[/math] had an age of 90.
- c) [math]\displaystyle{ B }[/math] fails 30 [math]\displaystyle{ tu }[/math] later at 235.
- 8. The system itself never failed.
Additional Rules and Assumptions for Load Sharing Containers
- 1. The option of whether components operate while the system is down is defined at the container level. Contained items inherit this property from the container. However, regardless of the container settings:
- a) If a path inside the container is down, blocks inside the container that are in that path do not continue to operate.
- b) Blocks that are up do not continue to operate while the container is down.
- 2. If a container brings the system down, the block that brought the container down is responsible for the system going down. (This is the opposite of standby containers.)
- 3. The duty cycle for a load sharing container is defined at the container level. Contained items inherit this property from the container.
- 1. The option of whether components operate while the system is down is defined at the container level. Contained items inherit this property from the container. However, regardless of the container settings:
Discussion
Even though the examples and explanations presented here are deterministic, the sequence of events and logic used to view the system is the same as the one that would be used during simulation. The difference is that the process would be repeated multiple times during simulation and the results presented would be the average results over the multiple runs.
Additionally, multiple metrics and results are presented and defined in this chapter. Many of these results can also be used to obtain additional metrics not explicitly given in BlockSim's Simulation Results Explorer. As an example, to compute mean availability with inspections but without PMs, the explicit downtimes given for each event could be used. Furthermore, all of the results given are for operating times starting at zero to a specified and time (although the components themselves could have been defined with a non-zero starting age). Results for a starting time other than zero could be obtained by running two simulations and looking at the difference in the detailed results where applicable. As an example, the difference in uptimes and downtimes can be used to determine availabilities for a specific time window.