Parameter Estimation

Parameter Estimation

Parameter estimation refers to the process of using sample data (in our case times-to-failure or suceess data) to estimate the parameters of the selected distribution. Several parameter estimation methods are available. This section presents an overview of the available methods used in life data analysis. More specidically we start with the relatively simple method of probability plotting and continues with the more sophisticated methods of rank regression ( or least squares) and maximum likelihood.

Probability Plotting

The least mathematically intensive method for parameter estimation is the method of probability plotting. As the term implies, probability plotting involves a physical plot of the data on specially constructed probability plotting paper. This method is easily implemented by hand, given that one can obtain the appropriate probability plotting paper. The method of probability plotting takes the [math]\displaystyle{ cdf }[/math] of the distribution and attempts to linearize it by employing a specially constructed paper. For example, in the case of the two-parameter Weibull distribution, the [math]\displaystyle{ cdf }[/math] and unreliability [math]\displaystyle{ Q(T), }[/math] can be shown to be:

[math]\displaystyle{ F(T)=Q(T)=1-{e^{-(\tfrac{T}{\eta})^{\beta}}} }[/math]

This function can then be linearized (i.e. put in the common form of [math]\displaystyle{ y=ax+b }[/math] format) as follows:

[math]\displaystyle{ \begin{align} Q(T)= & 1-{e^{-(\tfrac{T}{\eta})^{\beta}}} \\ \ln (1-Q(T))= & \ln {e^{-(\tfrac{T}{\eta})^{\beta}}} \\ \ln (1-Q(T))=& -(\tfrac{T}{\eta})^{\beta} \\ \ln ( -\ln (1-Q(T)))= & \beta (\ln( \frac{T}{\eta })) \\ \ln ( \ln( \frac{1}{1-Q(T)}) = & \beta\ln{ T} -\beta(\eta ) \\ \end{align} }[/math]

Then setting:

[math]\displaystyle{ y=\ln \left( \ln \left( \frac{1}{1-Q(T)} \right) \right) }[/math]

and:

[math]\displaystyle{ x=\ln \left( T \right) }[/math]

the equation can be rewritten as,

[math]\displaystyle{ y=\beta x-\beta \ln \left( \eta \right) }[/math]

which is now a linear equation with a slope of [math]\displaystyle{ \beta }[/math] and an intercept of [math]\displaystyle{ \beta ln(\eta) }[/math].
The next task is to construct a paper with the appropriate [math]\displaystyle{ y }[/math] - and [math]\displaystyle{ x }[/math] -axes. The x-axis calculation is easy since it is simply logarithmic. The y-axis, however, has to represent,

[math]\displaystyle{ y=\ln (\ln ( \frac{1}{1-Q(T)} ))) }[/math]

where [math]\displaystyle{ Q(T) }[/math] is the unreliability (or a double log reciprocal scale). Such papers have been created by different vendors and are called probability plotting papers.
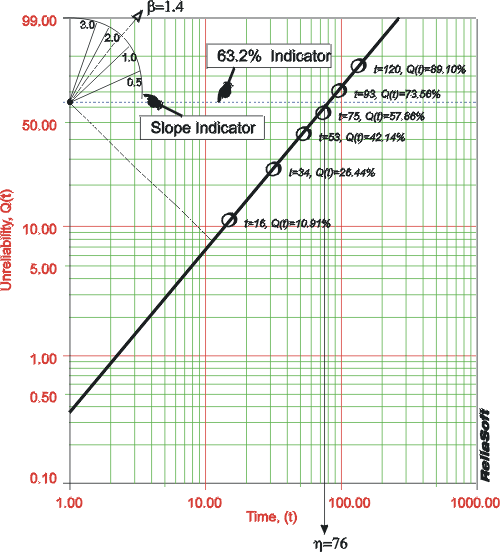
To illustrate, consider the following probability plot on a Weibull probability paper.

This paper is constructed based on the mentioned [math]\displaystyle{ y }[/math] - and [math]\displaystyle{ x }[/math] -transformations, where the y-axis represents unreliability and the x-axis represents time. Both of these values must be known for each time-to-failure point we want to plot. Then, given the [math]\displaystyle{ y }[/math] and [math]\displaystyle{ x }[/math] value for each point, the points can easily be put on the plot. Once the points have been placed on the plot, the best possible straight line is drawn through these points. Once the line has been drawn, the slope of the line can be obtained (some probability papers include a slope indicator to simplify this calculation). This is the parameter [math]\displaystyle{ \beta, }[/math] which is the value of the slope. To determine the scale parameter, [math]\displaystyle{ \eta }[/math] (also called the characteristic life by some authors), one must simply set [math]\displaystyle{ t = \eta }[/math] in the [math]\displaystyle{ cdf }[/math] equation.

Note that from before:

so at [math]\displaystyle{ T=\eta }[/math]

[math]\displaystyle{ \begin{align} Q(T)= & 1-{{e}^{-{{\left( \tfrac{\eta }{\eta } \right)}^{\beta }}}} \\ = & 1-{{e}^{-1}} \\ = & 0.632 \\ = & 63.2% \end{align} }[/math]

Thus, if we enter the [math]\displaystyle{ y }[/math] axis at [math]\displaystyle{ Q(T)=63.2%, }[/math] the corresponding value of [math]\displaystyle{ T }[/math]will be equal to [math]\displaystyle{ \eta . }[/math] Thus, using this simple but rather time-consuming methodology, the parameters of the Weibull distribution can be estimated.

Determining the [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] Position of the Plot Points

The points on the plot represent our data or, more specifically, our times-to-failure data. If, for example, we tested four units that failed at 10, 20, 30 and 40 hours, we would use these times as our [math]\displaystyle{ x }[/math] values or time values. Determining what the appropriate [math]\displaystyle{ y }[/math] plotting positions, or the unreliability values, should be is a little more complex. To determine the [math]\displaystyle{ y }[/math] plotting positions, we must first determine a value indicating the corresponding unreliability for that failure. In other words, we need to obtain the cumulative percent failed for each time-to-failure. In this example, and by 10 hours, the cumulative percent failed is 25%, by 20 hours 50%, and so forth. This is a simple method illustrating the idea. The problem with this simple method is the fact that the 100% point is not defined on most probability plots, thus an alternative and more robust approach must be used. The most widely used method of determining this value is the method of obtaining the median rank for each failure. This method is discussed next.

Median Ranks

Median ranks are used to obtain an estimate of the unreliability, [math]\displaystyle{ Q({T_j}) }[/math] for each failure. It is the value that the true probability of failure, [math]\displaystyle{ Q({{T}_{j}}), }[/math] should have at the [math]\displaystyle{ {{j}^{th}} }[/math] failure out of a sample of [math]\displaystyle{ N }[/math] units at a [math]\displaystyle{ 50% }[/math] confidence level. This essentially means that this is our best estimate for the unreliability. Half of the time the true value will be greater than the 50% confidence estimate, the other half of the time the true value will be less than the estimate. This estimate is based on a solution of the binomial equation.
The rank can be found for any percentage point, [math]\displaystyle{ P }[/math], greater than zero and less than one, by solving the cumulative binomial equation for [math]\displaystyle{ Z }[/math] . This represents the rank, or unreliability estimate, for the [math]\displaystyle{ {{j}^{th}} }[/math] failure[15; 16] in the following equation for the cumulative binomial:

[math]\displaystyle{ P=\underset{k=j}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} N \\ k \\ \end{matrix} \right){{Z}^{k}}{{\left( 1-Z \right)}^{N-k}} }[/math]

where [math]\displaystyle{ N }[/math] is the sample size and [math]\displaystyle{ j }[/math] the order number. The median rank is obtained by solving this equation for [math]\displaystyle{ Z }[/math] at [math]\displaystyle{ P=0.50, }[/math]

[math]\displaystyle{ 0.50=\underset{k=j}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} N \\ k \\ \end{matrix} \right){{Z}^{k}}{{\left( 1-Z \right)}^{N-k}} }[/math]

For example, if [math]\displaystyle{ N=4 }[/math] and we have four failures, we would solve the median rank equation, Eqn. (medrank), four times; once for each failure with [math]\displaystyle{ j= }[/math] 1, 2, 3 and 4, for the value of [math]\displaystyle{ Z. }[/math] This result can then be used as the unreliability estimate for each failure or the [math]\displaystyle{ y }[/math] plotting position. (The Weibull distribution chapter, Chapter 6, presents a step-by-step example for this method.) The solution of Eqn. (medrank) for [math]\displaystyle{ Z }[/math] requires the use of numerical methods. A more straightforward and easier method of estimating median ranks is by applying two transformations to Eqn. (medrank), first to the beta distribution and then to the F distribution, resulting in [12;13],

[math]\displaystyle{ \begin{array}{*{35}{l}} MR & = & \tfrac{1}{1+\tfrac{N-j+1}{j}{{F}_{0.50;m;n}}} \\ m & = & 2(N-j+1) \\ n & = & 2j \\ \end{array} }[/math]

[math]\displaystyle{ {F_{0.50;m;n}} }[/math] denotes the F distribution at the 0.50 point, with [math]\displaystyle{ m }[/math] and [math]\displaystyle{ n }[/math] degrees of freedom, for the [math]\displaystyle{ {{j}^{th}} }[/math] failure out of [math]\displaystyle{ N }[/math] units. Weibull++ uses this formulation when determining the median ranks.
Another quick, and less accurate, approximation of the median ranks is also given by [15]:

[math]\displaystyle{ MR = \frac{{j - 0.3}}{{N + 0.4}} }[/math]

This approximation of the median ranks is also known as Benard's approximation.

Kaplan-Meier

The Kaplan-Meier estimator is used as an alternative to the median ranks method for calculating the estimates of the unreliability for probability plotting purposes. The equation of the estimator is given by,

[math]\displaystyle{ \widehat{F}({{t}_{i}})=1-\underset{j=1}{\overset{i}{\mathop \prod }}\,\frac{{{n}_{j}}-{{r}_{j}}}{{{n}_{j}}},\text{ }i=1,...,m }[/math]

where,

[math]\displaystyle{ \begin{align} m = & {\text{total number of data points}} \\ n = & {\text{the total number of units}} \\ {n_i} = & n - \sum_{j = 0}^{i - 1}{s_j} - \sum_{j = 0}^{i - 1}{r_j}, \text{i = 1,...,m }\\ {r_j} = & {\text{ number of failures in the}}{j^{th}}{\text{ data group, and}} \\ {s_j} = & {\text{number of surviving units in the }}{j^{th}}{\text{ data group}} \\ \end{align} }[/math]

Weibull++ provides the option to select whether the median ranks or the Kaplan-Meier estimator is used for the unreliability estimates for probability plotting and regression. By default, the median ranks are used.

Probability Plots for Other Distributions

This same methodology can be applied to other distributions which have [math]\displaystyle{ cdf }[/math] equations that can be linearized. Different probability papers exist for each distribution, since different distributions have different [math]\displaystyle{ cdf }[/math] equations. Weibull++ automatically creates these plots for you when choosing a probability plot for a particular distribution. Special scales on these plots allow the parameter estimates to be derived directly from the plots, similar to the way [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \eta }[/math] were obtained from the Weibull probability plot. These will be discussed in subsequent chapters on the individual distributions.

Some Shortfalls of Manual Probability Plotting

Besides the most obvious drawback to probability plotting, which is the amount of effort required, manual probability plotting is not always consistent in the results. Two people plotting a straight line through a set of points will not always draw this line the same way, and thus will come up with slightly different results. This method was used primarily before the widespread use of computers that could easily perform the calculations for more complicated parameter estimation methods, such as the least squares and maximum likelihood methods.

Least Squares Parameter Estimation (Regression Analysis)

Using the idea of probability plotting, regression analysis mathematically fits the best straight line to a set of points, in an attempt to estimate the parameters. Essentially, this is a mathematically based version of the probability plotting method discussed previously.

Background Theory

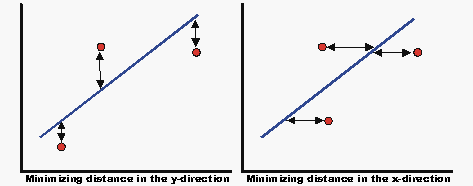
The method of linear least squares is used for all regression analysis performed by Weibull++, except for the cases of the three-parameter Weibull, mixed Weibull, gamma and generalized gamma distributions where a non-linear regression technique is employed. The terms linear regression and least squares are used synonymously in this reference. The term rank regression is used instead of least squares, or linear regression, because the regression is performed on the rank values, more specifically, the median rank values (represented on the y-axis). The method of least squares requires that a straight line be fitted to a set of data points, such that the sum of the squares of the distance of the points to the fitted line is minimized. This minimization can be performed in either the vertical or horizontal direction. If the regression is on [math]\displaystyle{ X }[/math], then the line is fitted so that the horizontal deviations from the points to the line are minimized. If the regression is on Y, then this means that the distance of the vertical deviations from the points to the line is minimized. This is illustrated in the following figure.

Rank Regression on [math]\displaystyle{ Y }[/math]

Assume that a set of data pairs [math]\displaystyle{ ({x_1},{y_1}) }[/math], [math]\displaystyle{ ({{x}_{2}},{{y}_{2}}) }[/math],..., [math]\displaystyle{ ({{x}_{N}},{{y}_{N}}) }[/math] were obtained and plotted, and that the [math]\displaystyle{ x }[/math] -values are known exactly. Then, according to the least squares principle, which minimizes the vertical distance between the data points and the straight line fitted to the data, the best fitting straight line to these data is the straight line [math]\displaystyle{ y=\hat{a}+\hat{b}x }[/math] (where the recently introduced [math]\displaystyle{ (\hat{ }) }[/math] symbol indicates that this value is an estimate) such that: .. and where [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat b }[/math] are the least squares estimates of [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math],and [math]\displaystyle{ N }[/math] is the number of data points. These equations are minimized by estimates of [math]\displaystyle{ \widehat a }[/math] and [math]\displaystyle{ \widehat{b} }[/math] such that:

[math]\displaystyle{ \hat{a}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}}{N}=\bar{y}-\hat{b}\bar{x} }[/math]

and:

[math]\displaystyle{ \hat{b}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}{{y}_{i}}-\tfrac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}}{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,x_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}} \right)}^{2}}}{N}} }[/math]

Rank Regression on X

Assume that a set of data pairs .., [math]\displaystyle{ ({x_2},{y_2}) }[/math],..., [math]\displaystyle{ ({x_N},{y_N}) }[/math]were obtained and plotted, and that the y-values are known exactly. The same least squares principle is applied, this time minimizing the horizontal distance between the data points and the straight line fitted to the data. The best fitting straight line to these data is the straight line [math]\displaystyle{ x=\widehat{a}+\widehat{b}y }[/math] such that:

[math]\displaystyle{ \underset{i=1}{\overset{N}{\mathop \sum }}\,{{(\widehat{a}+\widehat{b}{{y}_{i}}-{{x}_{i}})}^{2}}=min(a,b)\underset{i=1}{\overset{N}{\mathop \sum }}\,{{(a+b{{y}_{i}}-{{x}_{i}})}^{2}} }[/math]

Again, [math]\displaystyle{ \widehat{a} }[/math] and [math]\displaystyle{ \widehat b }[/math] are the least squares estimates of and [math]\displaystyle{ b, }[/math] and [math]\displaystyle{ N }[/math] is the number of data points. These equations are minimized by estimates of [math]\displaystyle{ \widehat a }[/math] and [math]\displaystyle{ \widehat{b} }[/math] such that:

[math]\displaystyle{ \hat{a}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}=\bar{x}-\hat{b}\bar{y} }[/math]

and:

[math]\displaystyle{ \widehat{b}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}{{y}_{i}}-\tfrac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}}{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,y_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}} \right)}^{2}}}{N}} }[/math]

The corresponding relations for determining the parameters for specific distributions (i.e., Weibull, exponential, etc.), are presented in the chapters covering that distribution.

The Correlation Coefficient

The correlation coefficient is a measure of how well the linear regression model fits the data and is usually denoted by [math]\displaystyle{ \rho }[/math]. In the case of life data analysis, it is a measure for the strength of the linear relation (correlation) between the median ranks and the data. The population correlation coefficient is defined as follows:

[math]\displaystyle{ \rho =\frac{{{\sigma }_{xy}}}{{{\sigma }_{x}}{{\sigma }_{y}}} }[/math]

where [math]\displaystyle{ {{\sigma }_{xy}}= }[/math] covariance of and [math]\displaystyle{ y }[/math] , [math]\displaystyle{ {{\sigma }_{x}}= }[/math] standard deviation of [math]\displaystyle{ x }[/math] , and [math]\displaystyle{ {\sigma _y} = }[/math] standard deviation of [math]\displaystyle{ y }[/math].

The estimator of [math]\displaystyle{ \rho }[/math] is the sample correlation coefficient, [math]\displaystyle{ \hat{\rho } }[/math], given by,

[math]\displaystyle{ \hat{\rho }=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}{{y}_{i}}-\tfrac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}}{\sqrt{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,x_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}} \right)}^{2}}}{N} \right)\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,y_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}} \right)}^{2}}}{N} \right)}} }[/math]

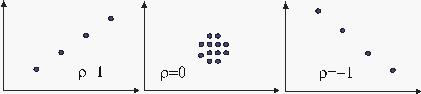
The range of [math]\displaystyle{ \hat \rho }[/math] is [math]\displaystyle{ -1\le \hat{\rho }\le 1. }[/math]

The closer the value is to [math]\displaystyle{ \pm 1 }[/math], the better the linear fit. Note that +1 indicates a perfect fit (the paired values ( [math]\displaystyle{ {{x}_{i}},{{y}_{i}} }[/math] ) lie on a straight line) with a positive slope, while -1 indicates a perfect fit with a negative slope. A correlation coefficient value of zero would indicate that the data are randomly scattered and have no pattern or correlation in relation to the regression line model.

Comments on the Least Squares Method

The least squares estimation method is quite good for functions that can be linearized. For these distributions, the calculations are relatively easy and straightforward, having closed-form solutions which can readily yield an answer without having to resort to numerical techniques or tables. Further, this technique provides a good measure of the goodness-of-fit of the chosen distribution in the correlation coefficient. Least squares is generally best used with data sets containing complete data, that is, data consisting only of single times-to-failure with no censored or interval data. Chapter 4 details the different data types, including complete, left censored, right censored (or suspended) and interval data.

MLE (Maximum Likelihood) Parameter Estimation for Complete Data

From a statistical point of view, the method of maximum likelihood estimation is, with some exceptions, considered to be the most robust of the parameter estimation techniques discussed here. This method is presented in this section for complete data, that is, data consisting only of single times-to-failure.

Background on Theory

The basic idea behind MLE is to obtain the most likely values of the parameters, for a given distribution, that will best describe the data. As an example, consider the following data (-3, 0, 4) and assume that you are trying to estimate the mean of the data. Now, if you have to choose the most likely value for the mean from -5, 1 and 10, which one would you choose? In this case, the most likely value is 1 (given your limit on choices). Similarly, under MLE, one determines the most likely values for the parameters of the assumed distribution.

It is mathematically formulated as follows:

If [math]\displaystyle{ x }[/math] is a continuous random variable with [math]\displaystyle{ pdf: }[/math]

[math]\displaystyle{ f(x;{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) }[/math]

where [math]\displaystyle{ {\theta _1},{\theta _2},...,{\theta _k} }[/math] are [math]\displaystyle{ k }[/math] unknown parameters which need to be estimated, with independent observations, , which correspond in the case of life data analysis to failure times. The likelihood function is given by:

[math]\displaystyle{ L({{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}|{{x}_{1}},{{x}_{2}},...,{{x}_{R}})=L=\underset{i=1}{\overset{R}{\mathop \prod }}\,f({{x}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) }[/math]

[math]\displaystyle{ i=1,2,...,R }[/math]

The logarithmic likelihood function is given by:

[math]\displaystyle{ \Lambda = \ln L =\sum_{i = 1}^R \ln f({x_i};{\theta _1},{\theta _2},...,{\theta _k}) }[/math]

The maximum likelihood estimators (or parameter values) of [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}, }[/math] are obtained by maximizing [math]\displaystyle{ L }[/math] or [math]\displaystyle{ \Lambda . }[/math]

By maximizing [math]\displaystyle{ \Lambda , }[/math] which is much easier to work with than [math]\displaystyle{ L }[/math], the maximum likelihood estimators (MLE) of [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}} }[/math] are the simultaneous solutions of [math]\displaystyle{ k }[/math] equations such that:

[math]\displaystyle{ \frac{\partial{\Lambda}}{\partial{\theta_j}}=0, \text{ j=1,2...,k} }[/math]

Even though it is common practice to plot the MLE solutions using median ranks (points are plotted according to median ranks and the line according to the MLE solutions), this is not completely representative. As can be seen from the equations above, the MLE method is independent of any kind of ranks. For this reason, the MLE solution often appears not to track the data on the probability plot. This is perfectly acceptable since the two methods are independent of each other, and in no way suggests that the solution is wrong.

Comments on the MLE Method

The MLE method has many large sample properties that make it attractive for use. It is asymptotically consistent, which means that as the sample size gets larger, the estimates converge to the right values. It is asymptotically efficient, which means that for large samples, it produces the most precise estimates. It is asymptotically unbiased, which means that for large samples one expects to get the right value on average. The distribution of the estimates themselves is normal, if the sample is large enough, and this is the basis for the usual Fisher Matrix confidence bounds discussed later. These are all excellent large sample properties.

Unfortunately, the size of the sample necessary to achieve these properties can be quite large: thirty to fifty to more than a hundred exact failure times, depending on the application. With fewer points, the methods can be badly biased. It is known, for example, that MLE estimates of the shape parameter for the Weibull distribution are badly biased for small sample sizes, and the effect can be increased depending on the amount of censoring. This bias can cause major discrepancies in analysis. There are also pathological situations when the asymptotic properties of the MLE do not apply. One of these is estimating the location parameter for the three-parameter Weibull distribution when the shape parameter has a value close to 1. These problems, too, can cause major discrepancies.

However, MLE can handle suspensions and interval data better than rank regression, particularly when dealing with a heavily censored data set with few exact failure times or when the censoring times are unevenly distributed. It can also provide estimates with one or no observed failures, which rank regression cannot do. As a rule of thumb, our recommendation is to use rank regression techniques when the sample sizes are small and without heavy censoring (censoring is discussed in Chapter 4). When heavy or uneven censoring is present, when a high proportion of interval data is present and/or when the sample size is sufficient, MLE should be preferred.

Bayesian Statistics

Up to this point, we have dealt exclusively with what is commonly referred to as classical statistics. In this section, another school of thought in statistical analysis will be introduced, namely Bayesian statistics. The premise of Bayesian statistics (within the context of life data analysis) is to incorporate prior knowledge, along with a given set of current observations, in order to make statistical inferences. The prior information could come from operational or observational data, from previous comparable experiments or from engineering knowledge. This type of analysis can be particularly useful when there is limited test data for a given design or failure mode but there is a strong prior understanding of the failure rate behavior for that design or mode. By incorporating prior information about the parameter(s), a posterior distribution for the parameter(s) can be obtained and inferences on the model parameters and their functions can be made. This section is intended to give a quick and elementary overview of Bayesian methods, focused primarily on the material necessary for understanding the Bayesian analysis methods available in Weibull++. Extensive coverage of the subject can be found in numerous books dealing with Bayesian statistics.

Bayes’s Rule

Bayes’s rule provides the framework for combining prior information with sample data. In this reference, we apply Bayes’s rule for combining prior information on the assumed distribution's parameter(s) with sample data in order to make inferences based on the model. The prior knowledge about the parameter(s) is expressed in terms of a [math]\displaystyle{ \varphi (\theta ), }[/math] called the prior distribution. The posterior distribution of [math]\displaystyle{ \theta }[/math] given the sample data, using Bayes rule, provides the updated information about the parameters [math]\displaystyle{ \theta }[/math]. This is expressed with the following posterior [math]\displaystyle{ pdf }[/math]:

[math]\displaystyle{ f(\theta |Data) = \frac{L(Data|\theta )\varphi (\theta )}{\int_{\zeta}^{} L(Data|\theta )\varphi(\theta )d (\theta)} }[/math]

where:

[math]\displaystyle{ \theta }[/math] is a vector of the parameters of the chosen distribution,

[math]\displaystyle{ \zeta }[/math] is the range of [math]\displaystyle{ \theta }[/math] ,

[math]\displaystyle{ L(Data|\theta) }[/math]is the likelihood function based on the chosen distribution and data

[math]\displaystyle{ \varphi(\theta ) }[/math] is the prior distribution for each of the parameters.

The integral in Eqn. (BayesRuleGeneral) is often referred to as the marginal probability and can be interpreted as the probability of obtaining the sample data given a prior distribution and it's a constant number. Generally, the integral in Eqn. (BayesRuleGeneral) does not have a closed form solution and numerical methods are needed for its solution.

As can be seen from Eqn. (BayesRuleGeneral), there is a significant difference between classical and Bayesian statistics. First, the idea of prior information does not exist in classical statistics. All inferences in classical statistics are based on the sample data. On the other hand, in the Bayesian framework, prior information constitutes the basis of the theory. Another difference is in the overall approach of making inferences and their interpretation. For example, in Bayesian analysis the parameters of the distribution to be fitted are the random variables. In reality, there is no distribution fitted to the data in the Bayesian case.

For instance, consider the case where data is obtained from a reliability test. Based on prior experience on a similar product, the analyst believes that shape parameter of the Weibull distribution has a value between [math]\displaystyle{ {\beta _1} }[/math] and [math]\displaystyle{ {{\beta }_{2}} }[/math] and wants to utilize this information. This can be achieved by using the Bayes theorem. At this point, the analyst is automatically forcing the Weibull distribution as a model for the data and with a shape parameter between [math]\displaystyle{ {\beta _1} }[/math] and [math]\displaystyle{ {\beta _2} }[/math]. In this example, the range of values for the shape parameter is the prior distribution, which in this case is Uniform. By applying Eqn. (BayesRuleGeneral), the posterior distribution of the shape parameter will be obtained. Thus, we end up with a distribution for the parameter rather than an estimate of the parameter, as in classical statistics.

To better illustrate the example, assume that a set of failure data was provided along with a distribution for the shape parameter (i.e. uniform prior) of the Weibull (automatically assuming that the data are Weibull distributed). Based on that, a new distribution (the posterior) for that parameter is then obtained using Eqn. (BayesRuleGeneral). This posterior distribution of the parameter may or may not resemble in form the assumed prior distribution. In other words, in this example the prior distribution of [math]\displaystyle{ \beta }[/math] was assumed to be uniform but the posterior is most likely not a uniform distribution.

The question now becomes: what is the value of the shape parameter? What about the reliability and other results of interest? In order to answer these questions, we have to remember that in the Bayesian framework all of these metrics are random variables. Therefore, in order to obtain an estimate, a probability needs to be specified or we can use the expected value of the posterior distribution.

In order to demonstrate the procedure of obtaining results from the posterior distribution, we will rewrite Eqn. (BayesRuleGeneral) for a single parameter [math]\displaystyle{ {\theta _1} }[/math]:

[math]\displaystyle{ f(\theta |Data) = \frac{L(Data|\theta_1 )\varphi (\theta_1 )}{\int_{\zeta}^{} L(Data|\theta_1 )\varphi(\theta_1 )d (\theta)} }[/math]

The expected value (or mean value) of the parameter [math]\displaystyle{ {{\theta }_{1}} }[/math] can be obtained using Eqns. (mean) and (BayesRuleSingle):

[math]\displaystyle{ E({\theta _1}) = {m_{{\theta _1}}} = \int_{\zeta}^{}{\theta _1} \cdot f({\theta _1}|Data)d{\theta _1} }[/math]

An alternative result for [math]\displaystyle{ {\theta _1} }[/math] would be the median value. Using Eqns. (median) and (BayesRuleSingle):

[math]\displaystyle{ \int_{-\infty ,0}^{{\theta }_{0.5}}f({{\theta }_{1}}|Data)d{{\theta }_{1}}=0.5 }[/math]

Eqn. (bayesMedian) is solved for [math]\displaystyle{ {\theta _{0.5}} }[/math] the median value of [math]\displaystyle{ {\theta _1} }[/math]

Similarly, any other percentile of the posterior [math]\displaystyle{ pdf }[/math] can be calculated and reported. For example, one could calculate the [math]\displaystyle{ 90th }[/math] percentile of [math]\displaystyle{ {\theta _1} }[/math]’s posterior [math]\displaystyle{ pdf }[/math]:

[math]\displaystyle{ \int_{-\infty ,0}^{{{\theta }_{0.9}}}f({{\theta }_{1}}|Data)d{{\theta }_{1}}=0.9 }[/math]

This calculation will be used in Chapter 5 for obtaining confidence bounds on the parameter(s).

The next step will be to make inferences on the reliability. Since the parameter [math]\displaystyle{ {\theta _1} }[/math] is a random variable described by the posterior [math]\displaystyle{ pdf, }[/math] all subsequent functions of [math]\displaystyle{ {{\theta }_{1}} }[/math] are distributed random variables as well and entirely based on the posterior [math]\displaystyle{ pdf }[/math] of [math]\displaystyle{ {{\theta }_{1}} }[/math]. Therefore, expected value, median or other percentile values will also need to be calculated. For example, the expected reliability at time [math]\displaystyle{ T }[/math] is:

[math]\displaystyle{ E[R(T|Data)] = \int_{\varsigma}^{} R(T)f(\theta |Data)d{\theta} }[/math]

In other words, at a given time [math]\displaystyle{ T }[/math], there is a distribution that governs the reliability value at that time, [math]\displaystyle{ T }[/math], and by using Eqn. (BayesRel), the expected (or mean) value of the reliability is obtained. Other percentiles of this distribution can also be obtained. A similar procedure is followed for other functions of [math]\displaystyle{ {\theta _1} }[/math], such as failure rate, reliable life, etc.

Prior Distributions

Prior distributions play a very important role in Bayesian Statistics. They are essentially the basis in Bayesian analysis. Different types of prior distributions exist, namely informative and non-informative. Non-informative prior distributions (a.k.a. vague, flat and diffuse) are distributions that have no population basis and play a minimal role in the posterior distribution. The idea behind the use of non-informative prior distributions is to make inferences that are not greatly affected by external information or when external information is not available. The uniform distribution is frequently used as a non-informative prior.

On the other hand, informative priors have a stronger influence on the posterior distribution. The influence of the prior distribution on the posterior is related to the sample size of the data and the form of the prior. Generally speaking, large sample sizes are required to modify strong priors, where weak priors are overwhelmed by even relatively small sample sizes. Informative priors are typically obtained from past data.