One Factor Designs
As explained in Simple Linear Regression Analysis and Multiple Linear Regression Analysis, the analysis of observational studies involves the use of regression models. The analysis of experimental studies involves the use of analysis of variance (ANOVA) models. For a comparison of the two models see Fitting ANOVA Models. In single factor experiments, ANOVA models are used to compare the mean response values at different levels of the factor. Each level of the factor is investigated to see if the response is significantly different from the response at other levels of the factor. The analysis of single factor experiments is often referred to as one-way ANOVA.
To illustrate the use of ANOVA models in the analysis of experiments, consider a single factor experiment where the analyst wants to see if the surface finish of certain parts is affected by the speed of a lathe machine. Data is collected for three speeds (or three treatments). Each treatment is replicated four times. Therefore, this experiment design is balanced. Surface finish values recorded using randomization are shown in the following table.
The ANOVA model for this experiment can be stated as follows:
- [math]\displaystyle{ {{Y}_{ij}}={{\mu }_{i}}+{{\epsilon }_{ij}}\,\! }[/math]
The ANOVA model assumes that the response at each factor level, [math]\displaystyle{ i\,\! }[/math], is the sum of the mean response at the [math]\displaystyle{ i\,\! }[/math]th level, [math]\displaystyle{ {{\mu }_{i}}\,\! }[/math], and a random error term, [math]\displaystyle{ {{\epsilon }_{ij}}\,\! }[/math]. The subscript [math]\displaystyle{ i\,\! }[/math] denotes the factor level while the subscript [math]\displaystyle{ j\,\! }[/math] denotes the replicate. If there are [math]\displaystyle{ {{n}_{a}}\,\! }[/math] levels of the factor and [math]\displaystyle{ m\,\! }[/math] replicates at each level then [math]\displaystyle{ i=1,2,...,{{n}_{a}}\,\! }[/math] and [math]\displaystyle{ j=1,2,...,m\,\! }[/math]. The random error terms, [math]\displaystyle{ {{\epsilon }_{ij}}\,\! }[/math], are assumed to be normally and independently distributed with a mean of zero and variance of [math]\displaystyle{ {{\sigma }^{2}}\,\! }[/math]. Therefore, the response at each level can be thought of as a normally distributed population with a mean of [math]\displaystyle{ {{\mu }_{i}}\,\! }[/math] and constant variance of [math]\displaystyle{ {{\sigma }^{2}}\,\! }[/math]. The equation given above is referred to as the means model.
The ANOVA model of the means model can also be written using [math]\displaystyle{ {{\mu }_{i}}=\mu +{{\tau }_{i}}\,\! }[/math], where [math]\displaystyle{ \mu \,\! }[/math] represents the overall mean and [math]\displaystyle{ {{\tau }_{i}}\,\! }[/math] represents the effect due to the [math]\displaystyle{ i\,\! }[/math]th treatment.
- [math]\displaystyle{ {{Y}_{ij}}=\mu +{{\tau }_{i}}+{{\epsilon }_{ij}}\,\! }[/math]
Such an ANOVA model is called the effects model. In the effects models the treatment effects, [math]\displaystyle{ {{\tau }_{i}}\,\! }[/math], represent the deviations from the overall mean, [math]\displaystyle{ \mu \,\! }[/math]. Therefore, the following constraint exists on the [math]\displaystyle{ {{\tau }_{i}}\,\! }[/math]s:
- [math]\displaystyle{ \underset{i=1}{\overset{{{n}_{a}}}{\mathop \sum }}\,{{\tau }_{i}}=0\,\! }[/math]
Fitting ANOVA Models
To fit ANOVA models and carry out hypothesis testing in single factor experiments, it is convenient to express the effects model of the effects model in the form [math]\displaystyle{ y=X\beta +\epsilon \,\! }[/math] (that was used for multiple linear regression models in Multiple Linear Regression Analysis). This can be done as shown next. Using the effects model, the ANOVA model for the single factor experiment in the first table can be expressed as:
- [math]\displaystyle{ {{Y}_{ij}}=\mu +{{\tau }_{i}}+{{\epsilon }_{ij}}\,\! }[/math]
where [math]\displaystyle{ \mu \,\! }[/math] represents the overall mean and [math]\displaystyle{ {{\tau }_{i}}\,\! }[/math] represents the [math]\displaystyle{ i\,\! }[/math]th treatment effect. There are three treatments in the first table (500, 600 and 700). Therefore, there are three treatment effects, [math]\displaystyle{ {{\tau }_{1}}\,\! }[/math], [math]\displaystyle{ {{\tau }_{2}}\,\! }[/math] and [math]\displaystyle{ {{\tau }_{3}}\,\! }[/math]. The following constraint exists for these effects:
- [math]\displaystyle{ \begin{align} \underset{i=1}{\overset{3}{\mathop \sum }}\,{{\tau }_{i}}= & 0 \\ \text{or } {{\tau }_{1}}+{{\tau }_{2}}+{{\tau }_{3}}= & 0 \end{align}\,\! }[/math]
For the first treatment, the ANOVA model for the single factor experiment in the above table can be written as:
- [math]\displaystyle{ {{Y}_{1j}}=\mu +{{\tau }_{1}}+0\cdot {{\tau }_{2}}+0\cdot {{\tau }_{3}}+{{\epsilon }_{1j}}\,\! }[/math]
Using [math]\displaystyle{ {{\tau }_{3}}=-({{\tau }_{1}}+{{\tau }_{2}})\,\! }[/math], the model for the first treatment is:
- [math]\displaystyle{ \begin{align} {{Y}_{1j}}= & \mu +{{\tau }_{1}}+0\cdot {{\tau }_{2}}-0\cdot ({{\tau }_{1}}+{{\tau }_{2}})+{{\epsilon }_{1j}} \\ \text{or }{{Y}_{1j}}= & \mu +{{\tau }_{1}}+0\cdot {{\tau }_{2}}+{{\epsilon }_{1j}} \end{align}\,\! }[/math]
Models for the second and third treatments can be obtained in a similar way. The models for the three treatments are:
- [math]\displaystyle{ \begin{align} \text{First Treatment}: & {{Y}_{1j}}=1\cdot \mu +1\cdot {{\tau }_{1}}+0\cdot {{\tau }_{2}}+{{\epsilon }_{1j}} \\ \text{Second Treatment}: & {{Y}_{2j}}=1\cdot \mu +0\cdot {{\tau }_{1}}+1\cdot {{\tau }_{2}}+{{\epsilon }_{2j}} \\ \text{Third Treatment}: & {{Y}_{3j}}=1\cdot \mu -1\cdot {{\tau }_{1}}-1\cdot {{\tau }_{2}}+{{\epsilon }_{3j}} \end{align}\,\! }[/math]
The coefficients of the treatment effects [math]\displaystyle{ {{\tau }_{1}}\,\! }[/math] and [math]\displaystyle{ {{\tau }_{2}}\,\! }[/math] can be expressed using two indicator variables, [math]\displaystyle{ {{x}_{1}}\,\! }[/math] and [math]\displaystyle{ {{x}_{2}}\,\! }[/math], as follows:
- [math]\displaystyle{ \begin{align} \text{Treatment Effect }{{\tau }_{1}}: & {{x}_{1}}=1,\text{ }{{x}_{2}}=0 \\ \text{Treatment Effect }{{\tau }_{2}}: & {{x}_{1}}=0,\text{ }{{x}_{2}}=1\text{ } \\ \text{Treatment Effect }{{\tau }_{3}}: & {{x}_{1}}=-1,\text{ }{{x}_{2}}=-1\text{ } \end{align}\,\! }[/math]
Using the indicator variables [math]\displaystyle{ {{x}_{1}}\,\! }[/math] and [math]\displaystyle{ {{x}_{2}}\,\! }[/math], the ANOVA model for the data in the first table now becomes:
- [math]\displaystyle{ Y=\mu +{{x}_{1}}\cdot {{\tau }_{1}}+{{x}_{2}}\cdot {{\tau }_{2}}+\epsilon \,\! }[/math]
The equation can be rewritten by including subscripts [math]\displaystyle{ i\,\! }[/math] (for the level of the factor) and [math]\displaystyle{ j\,\! }[/math] (for the replicate number) as:
- [math]\displaystyle{ {{Y}_{ij}}=\mu +{{x}_{i1}}\cdot {{\tau }_{1}}+{{x}_{i2}}\cdot {{\tau }_{2}}+{{\epsilon }_{ij}}\,\! }[/math]
The equation given above represents the "regression version" of the ANOVA model.
Treat Numerical Factors as Qualitative or Quantitative?
It can be seen from the equation given above that in an ANOVA model each factor is treated as a qualitative factor. In the present example the factor, lathe speed, is a quantitative factor with three levels. But the ANOVA model treats this factor as a qualitative factor with three levels. Therefore, two indicator variables, [math]\displaystyle{ {{x}_{1}}\,\! }[/math] and [math]\displaystyle{ {{x}_{2}}\,\! }[/math], are required to represent this factor.
Note that in a regression model a variable can either be treated as a quantitative or a qualitative variable. The factor, lathe speed, would be used as a quantitative factor and represented with a single predictor variable in a regression model. For example, if a first order model were to be fitted to the data in the first table, then the regression model would take the form [math]\displaystyle{ {{Y}_{ij}}={{\beta }_{0}}+{{\beta }_{1}}{{x}_{i1}}+{{\epsilon }_{ij}}\,\! }[/math]. If a second order regression model were to be fitted, the regression model would be [math]\displaystyle{ {{Y}_{ij}}={{\beta }_{0}}+{{\beta }_{1}}{{x}_{i1}}+{{\beta }_{2}}x_{i1}^{2}+{{\epsilon }_{ij}}\,\! }[/math]. Notice that unlike these regression models, the regression version of the ANOVA model does not make any assumption about the nature of relationship between the response and the factor being investigated.
The choice of treating a particular factor as a quantitative or qualitative variable depends on the objective of the experimenter. In the case of the data of the first table, the objective of the experimenter is to compare the levels of the factor to see if change in the levels leads to a significant change in the response. The objective is not to make predictions on the response for a given level of the factor. Therefore, the factor is treated as a qualitative factor in this case. If the objective of the experimenter were prediction or optimization, the experimenter would focus on aspects such as the nature of relationship between the factor, lathe speed, and the response, surface finish, so that the factor should be modeled as a quantitative factor to make accurate predictions.
Expression of the ANOVA Model as Y = XΒ + ε
The regression version of the ANOVA model can be expanded for the three treatments and four replicates of the data in the first table as follows:
The corresponding matrix notation is:
- [math]\displaystyle{ y=X\beta +\epsilon \,\! }[/math]
- where
- [math]\displaystyle{ y=\left[ \begin{matrix} {{Y}_{11}} \\ {{Y}_{21}} \\ {{Y}_{31}} \\ {{Y}_{12}} \\ {{Y}_{22}} \\ . \\ . \\ . \\ {{Y}_{34}} \\ \end{matrix} \right]=X\beta +\epsilon =\left[ \begin{matrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 1 & -1 & -1 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \\ . & . & . \\ . & . & . \\ . & . & . \\ 1 & -1 & -1 \\ \end{matrix} \right]\left[ \begin{matrix} \mu \\ {{\tau }_{1}} \\ {{\tau }_{2}} \\ \end{matrix} \right]+\left[ \begin{matrix} {{\epsilon }_{11}} \\ {{\epsilon }_{21}} \\ {{\epsilon }_{31}} \\ {{\epsilon }_{12}} \\ {{\epsilon }_{22}} \\ . \\ . \\ . \\ {{\epsilon }_{34}} \\ \end{matrix} \right]\,\! }[/math]
- Thus:
- [math]\displaystyle{ \begin{align} y= & X\beta +\epsilon \\ & & \\ & \left[ \begin{matrix} 6 \\ 13 \\ 23 \\ 13 \\ 16 \\ . \\ . \\ . \\ 18 \\ \end{matrix} \right]= & \left[ \begin{matrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 1 & -1 & -1 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \\ . & . & . \\ . & . & . \\ . & . & . \\ 1 & -1 & -1 \\ \end{matrix} \right]\left[ \begin{matrix} \mu \\ {{\tau }_{1}} \\ {{\tau }_{2}} \\ \end{matrix} \right]+\left[ \begin{matrix} {{\epsilon }_{11}} \\ {{\epsilon }_{21}} \\ {{\epsilon }_{31}} \\ {{\epsilon }_{12}} \\ {{\epsilon }_{22}} \\ . \\ . \\ . \\ {{\epsilon }_{34}} \\ \end{matrix} \right] \end{align}\,\! }[/math]
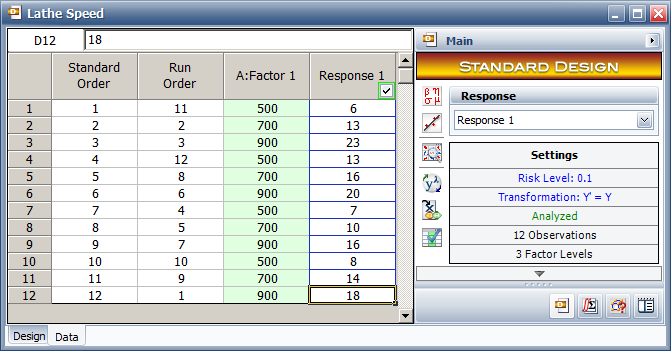
The matrices [math]\displaystyle{ y\,\! }[/math], [math]\displaystyle{ X\,\! }[/math] and [math]\displaystyle{ \beta \,\! }[/math] are used in the calculation of the sum of squares in the next section. The data in the first table can be entered into the DOE folio as shown in the figure below.
Hypothesis Test in Single Factor Experiments
The hypothesis test in single factor experiments examines the ANOVA model to see if the response at any level of the investigated factor is significantly different from that at the other levels. If this is not the case and the response at all levels is not significantly different, then it can be concluded that the investigated factor does not affect the response. The test on the ANOVA model is carried out by checking to see if any of the treatment effects, [math]\displaystyle{ {{\tau }_{i}}\,\! }[/math], are non-zero. The test is similar to the test of significance of regression mentioned in Simple Linear Regression Analysis and Multiple Linear Regression Analysis in the context of regression models. The hypotheses statements for this test are:
- [math]\displaystyle{ \begin{align} & {{H}_{0}}: & {{\tau }_{1}}={{\tau }_{2}}=...={{\tau }_{{{n}_{a}}}}=0 \\ & {{H}_{1}}: & {{\tau }_{i}}\ne 0\text{ for at least one }i \end{align}\,\! }[/math]
The test for [math]\displaystyle{ {{H}_{0}}\,\! }[/math] is carried out using the following statistic:
- [math]\displaystyle{ {{F}_{0}}=\frac{M{{S}_{TR}}}{M{{S}_{E}}}\,\! }[/math]
where [math]\displaystyle{ M{{S}_{TR}}\,\! }[/math] represents the mean square for the ANOVA model and [math]\displaystyle{ M{{S}_{E}}\,\! }[/math] is the error mean square. Note that in the case of ANOVA models we use the notation [math]\displaystyle{ M{{S}_{TR}}\,\! }[/math] (treatment mean square) for the model mean square and [math]\displaystyle{ S{{S}_{TR}}\,\! }[/math] (treatment sum of squares) for the model sum of squares (instead of [math]\displaystyle{ M{{S}_{R}}\,\! }[/math], regression mean square, and [math]\displaystyle{ S{{S}_{R}}\,\! }[/math], regression sum of squares, used in Simple Linear Regression Analysis and Multiple Linear Regression Analysis). This is done to indicate that the model under consideration is the ANOVA model and not the regression model. The calculations to obtain [math]\displaystyle{ M{{S}_{TR}}\,\! }[/math] and [math]\displaystyle{ S{{S}_{TR}}\,\! }[/math] are identical to the calculations to obtain [math]\displaystyle{ M{{S}_{R}}\,\! }[/math] and [math]\displaystyle{ S{{S}_{R}}\,\! }[/math] explained in Multiple Linear Regression Analysis.
Calculation of the Statistic [math]\displaystyle{ {{F}_{0}}\,\! }[/math]
The sum of squares to obtain the statistic [math]\displaystyle{ {{F}_{0}}\,\! }[/math] can be calculated as explained in Multiple Linear Regression Analysis. Using the data in the first table, the model sum of squares, [math]\displaystyle{ S{{S}_{TR}}\,\! }[/math], can be calculated as:
- [math]\displaystyle{ \begin{align} S{{S}_{TR}}= & {{y}^{\prime }}[H-(\frac{1}{{{n}_{a}}\cdot m})J]y \\ = & {{\left[ \begin{matrix} 6 \\ 13 \\ . \\ . \\ 18 \\ \end{matrix} \right]}^{\prime }}\left[ \begin{matrix} 0.1667 & -0.0833 & . & . & -0.0833 \\ -0.0833 & 0.1667 & . & . & -0.0833 \\ . & . & . & . & . \\ . & . & . & . & . \\ -0.0833 & -0.0833 & . & . & 0.1667 \\ \end{matrix} \right]\left[ \begin{matrix} 6 \\ 13 \\ . \\ . \\ 18 \\ \end{matrix} \right] \\ = & 232.1667 \end{align}\,\! }[/math]
In the previous equation, [math]\displaystyle{ {{n}_{a}}\,\! }[/math] represents the number of levels of the factor, [math]\displaystyle{ m\,\! }[/math] represents the replicates at each level, [math]\displaystyle{ y\,\! }[/math] represents the vector of the response values, [math]\displaystyle{ H\,\! }[/math] represents the hat matrix and [math]\displaystyle{ J\,\! }[/math] represents the matrix of ones. (For details on each of these terms, refer to Multiple Linear Regression Analysis.)
Since two effect terms, [math]\displaystyle{ {{\tau }_{1}}\,\! }[/math] and [math]\displaystyle{ {{\tau }_{2}}\,\! }[/math], are used in the regression version of the ANOVA model, the degrees of freedom associated with the model sum of squares, [math]\displaystyle{ S{{S}_{TR}}\,\! }[/math], is two.
- [math]\displaystyle{ dof(S{{S}_{TR}})=2\,\! }[/math]
The total sum of squares, [math]\displaystyle{ S{{S}_{T}}\,\! }[/math], can be obtained as follows:
- [math]\displaystyle{ \begin{align} S{{S}_{T}}= & {{y}^{\prime }}[I-(\frac{1}{{{n}_{a}}\cdot m})J]y \\ = & {{\left[ \begin{matrix} 6 \\ 13 \\ . \\ . \\ 18 \\ \end{matrix} \right]}^{\prime }}\left[ \begin{matrix} 0.9167 & -0.0833 & . & . & -0.0833 \\ -0.0833 & 0.9167 & . & . & -0.0833 \\ . & . & . & . & . \\ . & . & . & . & . \\ -0.0833 & -0.0833 & . & . & 0.9167 \\ \end{matrix} \right]\left[ \begin{matrix} 6 \\ 13 \\ . \\ . \\ 18 \\ \end{matrix} \right] \\ = & 306.6667 \end{align}\,\! }[/math]
In the previous equation, [math]\displaystyle{ I\,\! }[/math] is the identity matrix. Since there are 12 data points in all, the number of degrees of freedom associated with [math]\displaystyle{ S{{S}_{T}}\,\! }[/math] is 11.
- [math]\displaystyle{ dof(S{{S}_{T}})=11\,\! }[/math]
Knowing [math]\displaystyle{ S{{S}_{T}}\,\! }[/math] and [math]\displaystyle{ S{{S}_{TR}}\,\! }[/math], the error sum of squares is:
- [math]\displaystyle{ \begin{align} S{{S}_{E}}= & S{{S}_{T}}-S{{S}_{TR}} \\ = & 306.6667-232.1667 \\ = & 74.5 \end{align}\,\! }[/math]
The number of degrees of freedom associated with [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} dof(S{{S}_{E}})= & dof(S{{S}_{T}})-dof(S{{S}_{TR}}) \\ = & 11-2 \\ = & 9 \end{align}\,\! }[/math]
The test statistic can now be calculated using the equation given in Hypothesis Test in Single Factor Experiments as:
- [math]\displaystyle{ \begin{align} {{f}_{0}}= & \frac{M{{S}_{TR}}}{M{{S}_{E}}} \\ = & \frac{S{{S}_{TR}}/dof(S{{S}_{TR}})}{S{{S}_{E}}/dof(S{{S}_{E}})} \\ = & \frac{232.1667/2}{74.5/9} \\ = & 14.0235 \end{align}\,\! }[/math]
The [math]\displaystyle{ p\,\! }[/math] value for the statistic based on the [math]\displaystyle{ F\,\! }[/math] distribution with 2 degrees of freedom in the numerator and 9 degrees of freedom in the denominator is:
- [math]\displaystyle{ \begin{align} p\text{ }value= & 1-P(F\le {{f}_{0}}) \\ = & 1-0.9983 \\ = & 0.0017 \end{align}\,\! }[/math]
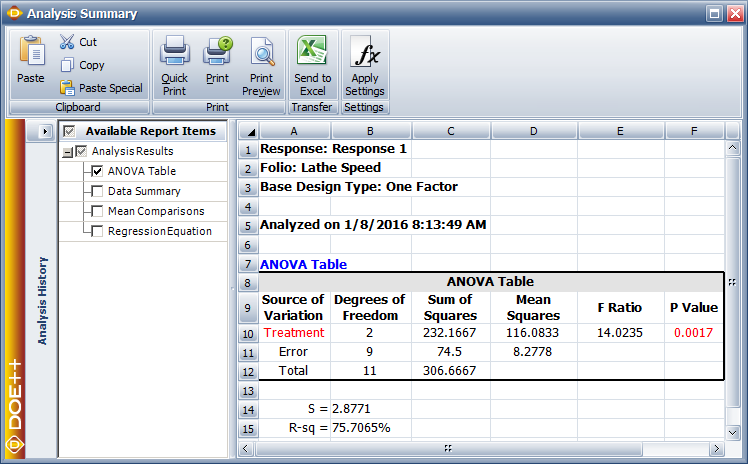
Assuming that the desired significance level is 0.1, since [math]\displaystyle{ p\,\! }[/math] value < 0.1, [math]\displaystyle{ {{H}_{0}}\,\! }[/math] is rejected and it is concluded that change in the lathe speed has a significant effect on the surface finish. The Weibull++ DOE folio displays these results in the ANOVA table, as shown in the figure below. The values of S and R-sq are the standard error and the coefficient of determination for the model, respectively. These values are explained in Multiple Linear Regression Analysis and indicate how well the model fits the data. The values in the figure below indicate that the fit of the ANOVA model is fair.
Confidence Interval on the ith Treatment Mean
The response at each treatment of a single factor experiment can be assumed to be a normal population with a mean of [math]\displaystyle{ {{\mu }_{i}}\,\! }[/math] and variance of [math]\displaystyle{ {{\sigma }^{2}}\,\! }[/math] provided that the error terms can be assumed to be normally distributed. A point estimator of [math]\displaystyle{ {{\mu }_{i}}\,\! }[/math] is the average response at each treatment, [math]\displaystyle{ {{\bar{y}}_{i\cdot }}\,\! }[/math]. Since this is a sample average, the associated variance is [math]\displaystyle{ {{\sigma }^{2}}/{{m}_{i}}\,\! }[/math], where [math]\displaystyle{ {{m}_{i}}\,\! }[/math] is the number of replicates at the [math]\displaystyle{ i\,\! }[/math]th treatment. Therefore, the confidence interval on [math]\displaystyle{ {{\mu }_{i}}\,\! }[/math] is based on the [math]\displaystyle{ t\,\! }[/math] distribution. Recall from Statistical Background on DOE (inference on population mean when variance is unknown) that:
- [math]\displaystyle{ \begin{align} {{T}_{0}}= & \frac{{{{\bar{y}}}_{i\cdot }}-{{\mu }_{i}}}{\sqrt{{{{\hat{\sigma }}}^{2}}/{{m}_{i}}}} \\ = & \frac{{{{\bar{y}}}_{i\cdot }}-{{\mu }_{i}}}{\sqrt{M{{S}_{E}}/{{m}_{i}}}} \end{align}\,\! }[/math]
has a [math]\displaystyle{ t\,\! }[/math] distribution with degrees of freedom [math]\displaystyle{ =dof(S{{S}_{E}})\,\! }[/math]. Therefore, a 100 ([math]\displaystyle{ 1-\alpha \,\! }[/math]) percent confidence interval on the [math]\displaystyle{ i\,\! }[/math]th treatment mean, [math]\displaystyle{ {{\mu }_{i}}\,\! }[/math], is:
- [math]\displaystyle{ {{\bar{y}}_{i\cdot }}\pm {{t}_{\alpha /2,dof(S{{S}_{E}})}}\sqrt{\frac{M{{S}_{E}}}{{{m}_{i}}}}\,\! }[/math]
For example, for the first treatment of the lathe speed we have:
- [math]\displaystyle{ \begin{align} {{{\hat{\mu }}}_{1}}= & {{{\bar{y}}}_{1\cdot }} \\ = & \frac{6+13+7+8}{4} \\ = & 8.5 \end{align}\,\! }[/math]
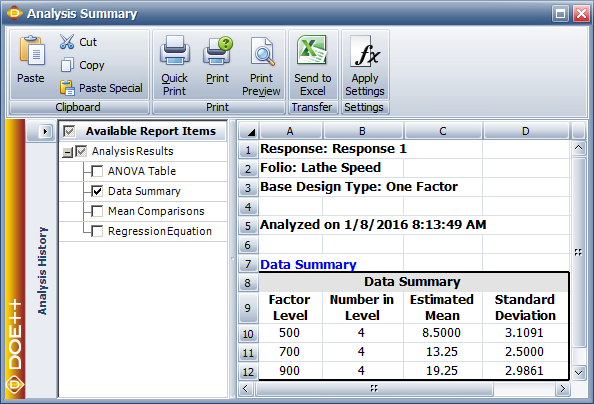
In the DOE folio, this value is displayed as the Estimated Mean for the first level, as shown in the Data Summary table in the figure below. The value displayed as the standard deviation for this level is simply the sample standard deviation calculated using the observations corresponding to this level. The 90% confidence interval for this treatment is:
- [math]\displaystyle{ \begin{align} = & {{{\bar{y}}}_{1\cdot }}\pm {{t}_{\alpha /2,dof(S{{S}_{E}})}}\sqrt{\frac{M{{S}_{E}}}{{{m}_{i}}}} \\ = & {{{\bar{y}}}_{1\cdot }}\pm {{t}_{0.05,9}}\sqrt{\frac{M{{S}_{E}}}{4}} \\ = & 8.5\pm 1.833\sqrt{\frac{(74.5/9)}{4}} \\ = & 8.5\pm 1.833(1.44) \\ = & 8.5\pm 2.64 \end{align}\,\! }[/math]
The 90% limits on [math]\displaystyle{ {{\mu }_{1}}\,\! }[/math] are 5.9 and 11.1, respectively.
Confidence Interval on the Difference in Two Treatment Means
The confidence interval on the difference in two treatment means, [math]\displaystyle{ {{\mu }_{i}}-{{\mu }_{j}}\,\! }[/math], is used to compare two levels of the factor at a given significance. If the confidence interval does not include the value of zero, it is concluded that the two levels of the factor are significantly different. The point estimator of [math]\displaystyle{ {{\mu }_{i}}-{{\mu }_{j}}\,\! }[/math] is [math]\displaystyle{ {{\bar{y}}_{i\cdot }}-{{\bar{y}}_{j\cdot }}\,\! }[/math]. The variance for [math]\displaystyle{ {{\bar{y}}_{i\cdot }}-{{\bar{y}}_{j\cdot }}\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} var({{{\bar{y}}}_{i\cdot }}-{{{\bar{y}}}_{j\cdot }})= & var({{{\bar{y}}}_{i\cdot }})+var({{{\bar{y}}}_{j\cdot }}) \\ = & {{\sigma }^{2}}/{{m}_{i}}+{{\sigma }^{2}}/{{m}_{j}} \end{align}\,\! }[/math]
For balanced designs all [math]\displaystyle{ {{m}_{i}}=m\,\! }[/math]. Therefore:
- [math]\displaystyle{ var({{\bar{y}}_{i\cdot }}-{{\bar{y}}_{j\cdot }})=2{{\sigma }^{2}}/m\,\! }[/math]
The standard deviation for [math]\displaystyle{ {{\bar{y}}_{i\cdot }}-{{\bar{y}}_{j\cdot }}\,\! }[/math] can be obtained by taking the square root of [math]\displaystyle{ var({{\bar{y}}_{i\cdot }}-{{\bar{y}}_{j\cdot }})\,\! }[/math] and is referred to as the pooled standard error:
- [math]\displaystyle{ \begin{align} Pooled\text{ }Std.\text{ }Error= & \sqrt{var({{{\bar{y}}}_{i\cdot }}-{{{\bar{y}}}_{j\cdot }})} \\ = & \sqrt{2{{{\hat{\sigma }}}^{2}}/m} \end{align}\,\! }[/math]
The [math]\displaystyle{ t\,\! }[/math] statistic for the difference is:
- [math]\displaystyle{ \begin{align} {{T}_{0}}= & \frac{{{{\bar{y}}}_{i\cdot }}-{{{\bar{y}}}_{j\cdot }}-({{\mu }_{i}}-{{\mu }_{j}})}{\sqrt{2{{{\hat{\sigma }}}^{2}}/m}} \\ = & \frac{{{{\bar{y}}}_{i\cdot }}-{{{\bar{y}}}_{j\cdot }}-({{\mu }_{i}}-{{\mu }_{j}})}{\sqrt{2M{{S}_{E}}/m}} \end{align}\,\! }[/math]
Then a 100 (1- [math]\displaystyle{ \alpha \,\! }[/math]) percent confidence interval on the difference in two treatment means, [math]\displaystyle{ {{\mu }_{i}}-{{\mu }_{j}}\,\! }[/math], is:
- [math]\displaystyle{ {{\bar{y}}_{i\cdot }}-{{\bar{y}}_{j\cdot }}\pm {{t}_{\alpha /2,dof(S{{S}_{E}})}}\sqrt{\frac{2M{{S}_{E}}}{m}}\,\! }[/math]
For example, an estimate of the difference in the first and second treatment means of the lathe speed, [math]\displaystyle{ {{\mu }_{1}}-{{\mu }_{2}}\,\! }[/math], is:
- [math]\displaystyle{ \begin{align} {{{\hat{\mu }}}_{1}}-{{{\hat{\mu }}}_{2}}= & {{{\bar{y}}}_{1\cdot }}-{{{\bar{y}}}_{2\cdot }} \\ = & 8.5-13.25 \\ = & -4.75 \end{align}\,\! }[/math]
The pooled standard error for this difference is:
- [math]\displaystyle{ \begin{align} Pooled\text{ }Std.\text{ }Error= & \sqrt{var({{{\bar{y}}}_{1\cdot }}-{{{\bar{y}}}_{2\cdot }})} \\ = & \sqrt{2{{{\hat{\sigma }}}^{2}}/m} \\ = & \sqrt{2M{{S}_{E}}/m} \\ = & \sqrt{\frac{2(74.5/9)}{4}} \\ = & 2.0344 \end{align}\,\! }[/math]
To test [math]\displaystyle{ {{H}_{0}}:{{\mu }_{1}}-{{\mu }_{2}}=0\,\! }[/math], the [math]\displaystyle{ t\,\! }[/math] statistic is:
- [math]\displaystyle{ \begin{align} {{t}_{0}}= & \frac{{{{\bar{y}}}_{1\cdot }}-{{{\bar{y}}}_{2\cdot }}-({{\mu }_{1}}-{{\mu }_{2}})}{\sqrt{2M{{S}_{E}}/m}} \\ = & \frac{-4.75-(0)}{\sqrt{\tfrac{2(74.5/9)}{4}}} \\ = & \frac{-4.75}{2.0344} \\ = & -2.3348 \end{align}\,\! }[/math]
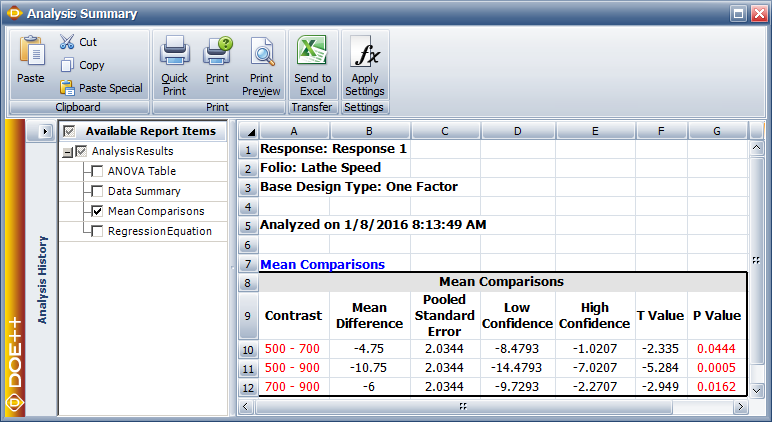
In the DOE folio, the value of the statistic is displayed in the Mean Comparisons table under the column T Value as shown in the figure below. The 90% confidence interval on the difference [math]\displaystyle{ {{\mu }_{1}}-{{\mu }_{2}}\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} = & {{{\bar{y}}}_{1\cdot }}-{{{\bar{y}}}_{2\cdot }}\pm {{t}_{\alpha /2,dof(S{{S}_{E}})}}\sqrt{\frac{2M{{S}_{E}}}{m}} \\ = & {{{\bar{y}}}_{1\cdot }}-{{{\bar{y}}}_{2\cdot }}\pm {{t}_{0.05,9}}\sqrt{\frac{2M{{S}_{E}}}{m}} \\ = & -4.75\pm 1.833\sqrt{\frac{2(74.5/9)}{4}} \\ = & -4.75\pm 1.833(2.0344) \\ = & -4.75\pm 3.729 \end{align}\,\! }[/math]
Hence the 90% limits on [math]\displaystyle{ {{\mu }_{1}}-{{\mu }_{2}}\,\! }[/math] are [math]\displaystyle{ -8.479\,\! }[/math] and [math]\displaystyle{ -1.021\,\! }[/math], respectively. These values are displayed under the Low CI and High CI columns in the following figure. Since the confidence interval for this pair of means does not included zero, it can be concluded that these means are significantly different at 90% confidence. This conclusion can also be arrived at using the [math]\displaystyle{ p\,\! }[/math] value noting that the hypothesis is two-sided. The [math]\displaystyle{ p\,\! }[/math] value corresponding to the statistic [math]\displaystyle{ {{t}_{0}}=-2.3348\,\! }[/math], based on the [math]\displaystyle{ t\,\! }[/math] distribution with 9 degrees of freedom is:
- [math]\displaystyle{ \begin{align} p\text{ }value= & 2\times (1-P(T\le |{{t}_{0}}|)) \\ = & 2\times (1-P(T\le 2.3348)) \\ = & 2\times (1-0.9778) \\ = & 0.0444 \end{align}\,\! }[/math]
Since [math]\displaystyle{ p\,\! }[/math] value < 0.1, the means are significantly different at 90% confidence. Bounds on the difference between other treatment pairs can be obtained in a similar manner and it is concluded that all treatments are significantly different.
Residual Analysis
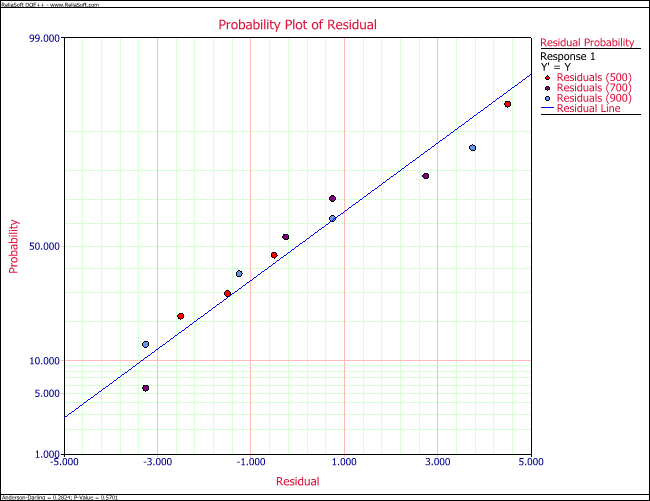
Plots of residuals, [math]\displaystyle{ {{e}_{ij}}\,\! }[/math], similar to the ones discussed in the previous chapters on regression, are used to ensure that the assumptions associated with the ANOVA model are not violated. The ANOVA model assumes that the random error terms, [math]\displaystyle{ {{\epsilon }_{ij}}\,\! }[/math], are normally and independently distributed with the same variance for each treatment. The normality assumption can be checked by obtaining a normal probability plot of the residuals.
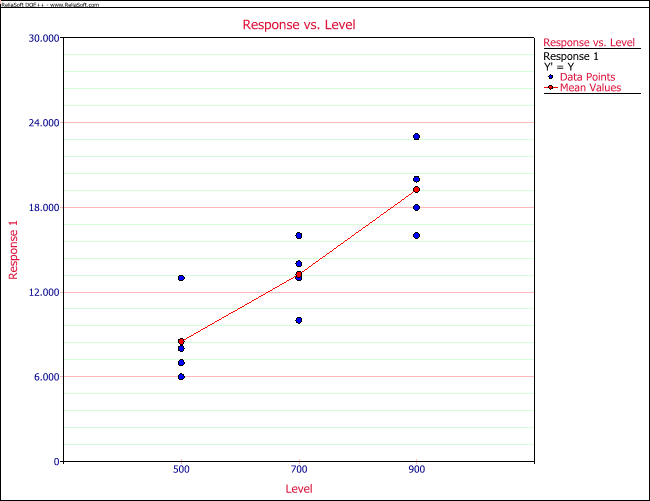
Equality of variance is checked by plotting residuals against the treatments and the treatment averages, [math]\displaystyle{ {{\bar{y}}_{i\cdot }}\,\! }[/math] (also referred to as fitted values), and inspecting the spread in the residuals. If a pattern is seen in these plots, then this indicates the need to use a suitable transformation on the response that will ensure variance equality. Box-Cox transformations are discussed in the next section. To check for independence of the random error terms residuals are plotted against time or run-order to ensure that a pattern does not exist in these plots. Residual plots for the given example are shown in the following two figures. The plots show that the assumptions associated with the ANOVA model are not violated.
Box-Cox Method
Transformations on the response may be used when residual plots for an experiment show a pattern. This indicates that the equality of variance does not hold for the residuals of the given model. The Box-Cox method can be used to automatically identify a suitable power transformation for the data based on the relationship:
- [math]\displaystyle{ {{Y}^{*}}={{Y}^{\lambda }}\,\! }[/math]
[math]\displaystyle{ \lambda \,\! }[/math] is determined using the given data such that [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] is minimized. The values of [math]\displaystyle{ {{Y}^{\lambda }}\,\! }[/math] are not used as is because of issues related to calculation or comparison of [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] values for different values of [math]\displaystyle{ \lambda \,\! }[/math]. For example, for [math]\displaystyle{ \lambda =0\,\! }[/math] all response values will become 1. Therefore, the following relationship is used to obtain [math]\displaystyle{ {{Y}^{\lambda }}\,\! }[/math] :
- [math]\displaystyle{ Y^{\lambda }=\left\{ \begin{array}{cc} \frac{y^{\lambda }-1}{\lambda \dot{y}^{\lambda -1}} & \lambda \neq 0 \\ \dot{y}\ln y & \lambda =0 \end{array} \right.\,\! }[/math]
where [math]\displaystyle{ \dot{y}={{\ln }^{-1}}[(1/n)\mathop{}_{}^{}\ln y]\,\! }[/math].
Once all [math]\displaystyle{ {{Y}^{\lambda }}\,\! }[/math] values are obtained for a value of [math]\displaystyle{ \lambda \,\! }[/math], the corresponding [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] for these values is obtained using [math]\displaystyle{ {{y}^{\lambda \prime }}[I-H]{{y}^{\lambda }}\,\! }[/math]. The process is repeated for a number of [math]\displaystyle{ \lambda \,\! }[/math] values to obtain a plot of [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] against [math]\displaystyle{ \lambda \,\! }[/math]. Then the value of [math]\displaystyle{ \lambda \,\! }[/math] corresponding to the minimum [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] is selected as the required transformation for the given data. The DOE folio plots [math]\displaystyle{ \ln S{{S}_{E}}\,\! }[/math] values against [math]\displaystyle{ \lambda \,\! }[/math] values because the range of [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] values is large and if this is not done, all values cannot be displayed on the same plot. The range of search for the best [math]\displaystyle{ \lambda \,\! }[/math] value in the software is from [math]\displaystyle{ -5\,\! }[/math] to [math]\displaystyle{ 5\,\! }[/math], because larger values of of [math]\displaystyle{ \lambda \,\! }[/math] are usually not meaningful. The DOE folio also displays a recommended transformation based on the best [math]\displaystyle{ \lambda \,\! }[/math] value obtained as per the second table.
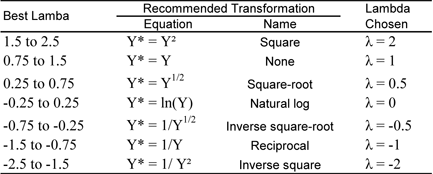
Confidence intervals on the selected [math]\displaystyle{ \lambda \,\! }[/math] values are also available. Let [math]\displaystyle{ S{{S}_{E}}(\lambda )\,\! }[/math] be the value of [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] corresponding to the selected value of [math]\displaystyle{ \lambda \,\! }[/math]. Then, to calculate the 100 (1- [math]\displaystyle{ \alpha \,\! }[/math]) percent confidence intervals on [math]\displaystyle{ \lambda \,\! }[/math], we need to calculate [math]\displaystyle{ S{{S}^{*}}\,\! }[/math] as shown next:
- [math]\displaystyle{ S{{S}^{*}}=S{{S}_{E}}(\lambda )\left( 1+\frac{t_{\alpha /2,dof(S{{S}_{E}})}^{2}}{dof(S{{S}_{E}})} \right)\,\! }[/math]
The required limits for [math]\displaystyle{ \lambda \,\! }[/math] are the two values of [math]\displaystyle{ \lambda \,\! }[/math] corresponding to the value [math]\displaystyle{ S{{S}^{*}}\,\! }[/math] (on the plot of [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] against [math]\displaystyle{ \lambda \,\! }[/math]). If the limits for [math]\displaystyle{ \lambda \,\! }[/math] do not include the value of one, then the transformation is applicable for the given data.
Note that the power transformations are not defined for response values that are negative or zero. The DOE folio deals with negative and zero response values using the following equations (that involve addition of a suitable quantity to all of the response values if a zero or negative response value is encountered).
- [math]\displaystyle{ \begin{align} y(i)& = y(i)+\left| {{y}_{\min }} \right|\times 1.1 & \text{Negative Response} \\ y(i)& = y(i)+1 & \text{Zero Response} \end{align}\,\! }[/math]
Here [math]\displaystyle{ {{y}_{\min }}\,\! }[/math] represents the minimum response value and [math]\displaystyle{ \left| {{y}_{\min }} \right|\,\! }[/math] represents the absolute value of the minimum response.
Example
To illustrate the Box-Cox method, consider the experiment given in the first table. Transformed response values for various values of [math]\displaystyle{ \lambda \,\! }[/math] can be calculated using the equation for [math]\displaystyle{ {Y}^{\lambda}\,\! }[/math] given in Box-Cox Method. Knowing the hat matrix, [math]\displaystyle{ H\,\! }[/math], [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] values corresponding to each of these [math]\displaystyle{ \lambda \,\! }[/math] values can easily be obtained using [math]\displaystyle{ {{y}^{\lambda \prime }}[I-H]{{y}^{\lambda }}\,\! }[/math]. [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] values calculated for [math]\displaystyle{ \lambda \,\! }[/math] values between [math]\displaystyle{ -5\,\! }[/math] and [math]\displaystyle{ 5\,\! }[/math] for the given data are shown below:
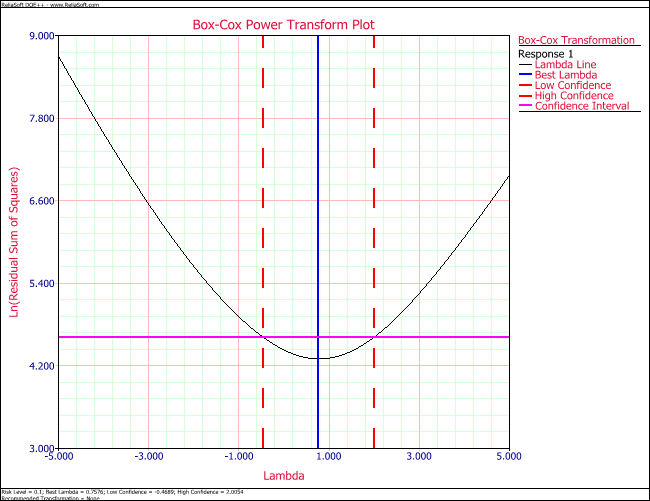
A plot of [math]\displaystyle{ \ln S{{S}_{E}}\,\! }[/math] for various [math]\displaystyle{ \lambda \,\! }[/math] values, as obtained from the DOE folio, is shown in the following figure. The value of [math]\displaystyle{ \lambda \,\! }[/math] that gives the minimum [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] is identified as 0.7841. The [math]\displaystyle{ S{{S}_{E}}\,\! }[/math] value corresponding to this value of [math]\displaystyle{ \lambda \,\! }[/math] is 73.74. A 90% confidence interval on this [math]\displaystyle{ \lambda \,\! }[/math] value is calculated as follows. [math]\displaystyle{ S{{S}^{*}}\,\! }[/math] can be obtained as shown next:
- [math]\displaystyle{ \begin{align} S{{S}^{*}}= & S{{S}_{E}}(\lambda )\left( 1+\frac{t_{\alpha /2,dof(S{{S}_{E}})}^{2}}{dof(S{{S}_{E}})} \right) \\ = & 73.74\left( 1+\frac{t_{0.05,9}^{2}}{9} \right) \\ = & 73.74\left( 1+\frac{{{1.833}^{2}}}{9} \right) \\ = & 101.27 \end{align}\,\! }[/math]
Therefore, [math]\displaystyle{ \ln S{{S}^{*}}=4.6178\,\! }[/math]. The [math]\displaystyle{ \lambda \,\! }[/math] values corresponding to this value from the following figure are [math]\displaystyle{ -0.4689\,\! }[/math] and [math]\displaystyle{ 2.0054\,\! }[/math]. Therefore, the 90% confidence limits on are [math]\displaystyle{ -0.4689\,\! }[/math] and [math]\displaystyle{ 2.0054\,\! }[/math]. Since the confidence limits include the value of 1, this indicates that a transformation is not required for the data in the first table.