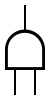
AND Gate

This page describes the AND gate and it's applications in Fault Tree diagrams used in Reliability and Safety Engineering.

In an AND gate, the output event occurs if all input events occur (or event A AND event B AND event C). When used in reliability and safety engineering an event is usualy a failure, a failure mode, or other undesirable event.

If one is looking at system reliability with each event represnting a component of the system then this this implies that all components must fail (input) in order for the system to fail (output). When using RBDs, the equivalent is a simple parallel configuration.

System Reliability Example

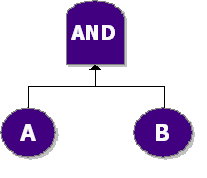
Consider a system with two components, A and B. The system fails if both A and B fail. Then the fault tree diagram is an AND gate (represinting the system level) with two events A and B. This is shown in the next figure.

Assuming independence then the reliability equation for either configuration is:

[math]\displaystyle{ {{R}_{System}}={{R}_{A}}+{{R}_{B}}-{{R}_{A}}\cdot {{R}_{B}} }[/math]

If we assume that the Relaibility of A is 0.90 and of B 0.85 then

[math]\displaystyle{ {{R}_{System}}=0.90+0.85-0.90\cdot 0.85 }[/math]

[math]\displaystyle{ {{R}_{System}}=0.985 }[/math]

Reliability deals with the probability of an event not occuring (the event being probability of failure of A, or Q(A)=P(A)), then if we are dealing directly with probabilities then P(A and B) = P(A ∩ B) = P(A) P(B).

[math]\displaystyle{ {{Q}_{System}}={{Q}_{A}}\cdot {{Q}_{B}} }[/math]

or

[math]\displaystyle{ {{Q}_{System}}=(1-0.90)\cdot (1-0.85) }[/math]

[math]\displaystyle{ {{Q}_{System}}=(0.015 }[/math].

Recall that

[math]\displaystyle{ {{R}_{System}}=1-{{Q}_{System}} }[/math]

[math]\displaystyle{ {{R}_{System}}=1-{0.015}=0.985. }[/math].