New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at BlockSim examples and BlockSim reference examples.
This example validates the results for complex systems in BlockSim's analytical and simulation diagrams.
Reference Case
The data set is from example 4.9 on page 85 in the book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.
Data
Some systems are made up of independent series, parallel, series, series-parallel, parallel-series, k-out-of-n, and redundant subsystems. The reliability of such an engineering system (presented in Figure 4.17 on page 85 of the book) is computed at 600 hours of mission time. Each component has an exponential life distribution model with a different lambda. Failures rates are presented in the table below.
| Components of the System
|
Number of Failures, [math]\displaystyle{ \lambda }[/math]
(x10-4 per hour)
|
| Component 1 |
1.2
|
| Component 2 |
2.3
|
| Component 3 |
0.9
|
| Component 4 |
1.6
|
| Component 5 |
4.8
|
| Component 6 |
3.3
|
| Component 7 |
1.7
|
| Component 8 |
2.5
|
| Component 9 |
4.3
|
| Component 10 |
4.3
|
Result
This example is solved by the system reduction method, which involves collapsing a system sequentially into the foregoing susbsystems, each represented by an equivalent reliability block, until the entire system is represented by a single reliability block. The system reliability is calculated as 93.67%.
Results in BlockSim
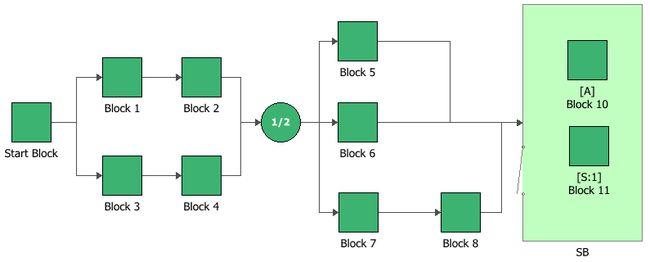
In BlockSim, the engineering system RBD is configured as shown below.
Each component is modeled using an exponential distribution with the corresponding lambda (failure rates) given in the table.
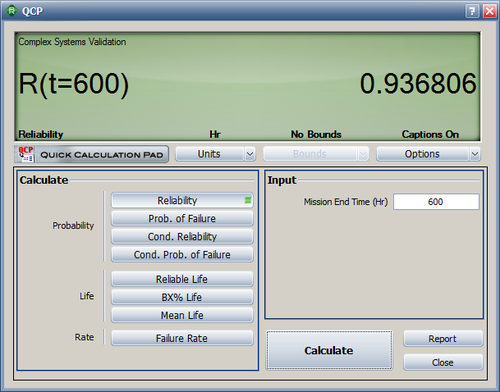
Analytical Proof
The reliability of the system at a mission time of 600 hours is calculated in the QCP as 93.68%. The difference of 0.01% is due to rounding errors and is negligible.
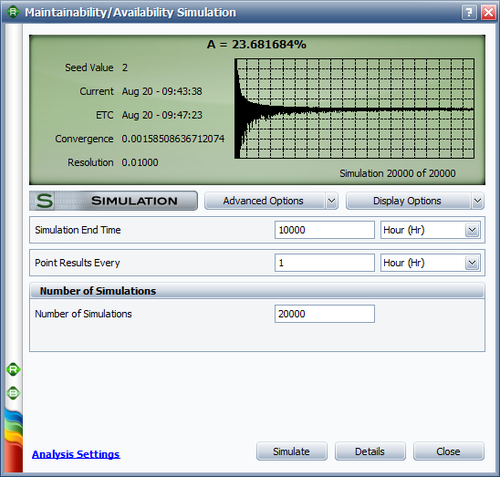
Simulation Proof
We can also estimate the results by using the simulation tool in BlockSim. The simulation settings are shown below.
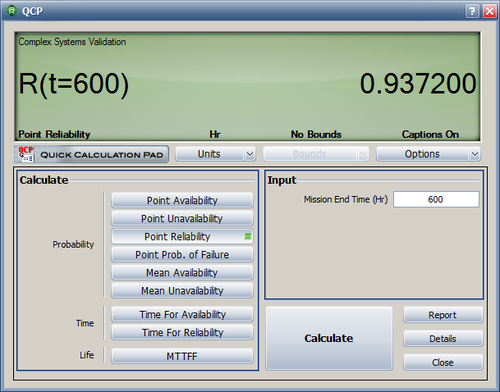
The point reliability of the system at a mission time of 600 hours is calculated as 93.72%.