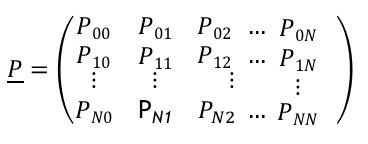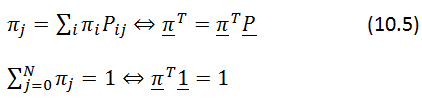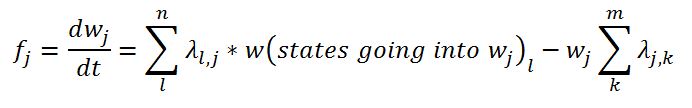Markov Diagrams

The term “Markov Chain", invented by Russian mathematician Andrey Markov, is used across many applications to represent a stochastic process made up of a sequence of random variables representing the evolution of a system, where the future state only depends on the current state of the system as past and future states are independent. Events are “chained” or “linked” serially together though memoryless transitions from one state to another. The term memoryless is used because past events are forgotten as they are irrelevant since an event or state is only dependent on the state or event that immediately preceded it.

Concept and Methodology

The concept behind the method is that given a system of states with transitions between them the analysis will give the probability of being in a particular state at a particular time. If some of the states are considered to be unavailable states for the system, then availability/reliability analysis can be performed for the system as a whole.

Discrete Markov Chains: Limiting Probabilities

Transition Matrix

A system has finitely many states {0, 1, 2…,N} and transition from state to state is random. The matrix shows the potential inputs and outputs from one state to another to describe transitions of a Markov chain. P(X_(n+1)=j│X,_n=i)=P_ij where 0≦P_ij≦1

Markov Chain Diagram

Markov Chain State diagrams can be used to label events and transitions based upon a transition matrix.

Chapman-Kolmogorov Equation

The Chapman-Kolmogorov Equation was realized and defined independently by British mathematician Sydney Chapman and Russian mathematician Andrew Kolmogorov. It can be used to provide the transitional densities of a Markov sequence.

Let p_i⁽ⁿ⁾=P(X_n=i), then

P(X_(n+1)=j) = [math]\displaystyle{ \sum_{i \mathop =0}^{N}P }[/math] (X_n+1 = j|X_n = i)

so P_j⁽ⁿ⁺¹⁾ = [math]\displaystyle{ \sum_{i \mathop =0}^{N}P }[/math] (X_i⁽ⁿ⁾ P_ij

With vector notation [math]\displaystyle{ \underline{p} }[/math]⁽ⁿ⁾ = (p₀⁽ⁿ⁾,p₁⁽ⁿ⁾, ... ,p_N⁽ⁿ⁾) (row vector)

[math]\displaystyle{ \underline{p} }[/math]⁽ⁿ⁺¹⁾ = p⁽ⁿ⁾[math]\displaystyle{ \underline{P} }[/math] = ([math]\displaystyle{ \underline{p} }[/math]^(n-1)[math]\displaystyle{ \underline{P} }[/math]² = p⁽⁰⁾p⁽ⁿ⁺¹⁾

Let P_ij^(m) = P (X_n+m = j| X_n = i) and [math]\displaystyle{ \underline{p} }[/math]^(m) = P_ij^(m)

then [math]\displaystyle{ \underline{P} }[/math]^n+m = [math]\displaystyle{ \underline{P} }[/math]⁽ⁿ⁾ * [math]\displaystyle{ \underline{P} }[/math]^(m) and [math]\displaystyle{ \underline{P} }[/math]⁽ⁿ⁾= [math]\displaystyle{ \underline{P} }[/math]ⁿ

Accessible and Communicating States

State j is accessible from state i, if for some m,

P_ij^(m) > 0

State i communicates with state j, if j is accessible from i and also state i is accessible from j:

[math]\displaystyle{ \sum_{m \mathop =1}^{\infty}P }[/math]_ij^(m) and [math]\displaystyle{ \sum_{m \mathop =1}^{\infty}P }[/math]_ji^(m)

Markov chain is irreducible if every state i communicates with all other states and with itself.

Recurrent and Transient States

Let f_i = P (starting at state i, system will return to state i) If f_i = 1, then state i is recurrent , repeated infinitely often If f_i < 1, then state i is transient , repeated returns have smaller and smaller probabilities.

f_i = [math]\displaystyle{ \sum_{m \mathop =1}^{\infty}P }[/math]_ii^(m)

Markov chain is ergodic, if all states are recurrent and not periodic (there is no d>0 such that P_ii^(m) > 0 if and only if m is multiple of d)

Limiting Probabilities

• Theorem:

For an irreducible, ergodic Markov chain [math]\displaystyle{ \lim_{m \to \infty}P }[/math]_ij^(m) = π_j for all j for all j (10.4) and limit is independent of i( steady state probabilities):

0 ≦ π_j≦ 1

• Method:

Mean Time Spent in States

Mean time spent in recurrent states = ∞ Mean time spent in transient states : S_ij = Starting at state i , expected number of time periods that state is j S_ij =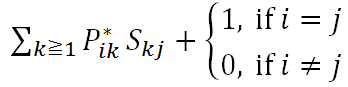

where P * contains rows and columns of transient states of matrix ▁P: S = I + P* S [math]\displaystyle{ \underline{S} }[/math] = (I-P *)^-1

Continuous Markov Chains: Applications to Non-Repairable Systems

• Non-repairable component with failure rate λ
  • P0(t) = P ( at time t component works)
  • P1(t) = P ( at time t component is broken)

P0 (t+ ∆ t) = (1- λ ∆ t) P0 (t) +0 P1 (t) Does not fail during ∆ t times

P1(t+ ∆ t) = λ ∆ t P0 (t) + 1 P1 (t) since P (Fails in ∆ Time) =1- e^{- λ∆t} ≈ 1- (1- [math]\displaystyle{ \tfrac{\lambda\Delta(t)}{1!}+\tfrac{(\lambda^2(\Delta(t))^2)}{2!} }[/math] - …) ≈ λ∆t if ∆t is small

Method

The method employed to solve a continuous Markov Chain problem will be a modified RK45 Runga-Kutta-Fehlberg, which is an adaptive step size Runga-Kutta method.

User Inputs

The user must provide initial probabilities for each state (must add up to exactly 1.0), and a transition probability between each state. If a transition probability is not given, it should be assumed to be zero.

Symbol Definitions

• α_j,0 is the initial probability of being in state j (given by the user).
• ε is the user defined tolerance (accuracy). Default should be 1e^-5 and can only get smaller.
• λ_l,j is the transitional failure rate into state w_j from state w_l
• w_l is the probability of being in the state associated with the λ_l,j’s
• λ_j,k is the transitional failure rate leaving state w_j to state w_k
• f_j is the change in state probability function (for a given state w_j):
  • 

f_j is not a function of time as only constant failure rates will be allowed in initial version. This means that the various k’s calculated during the RK45 method are only functions of all the w’s and the constant failure rates, λ’s.

Here's the formula for the Runge-Kutta-Fehlberg method (RK45).

w₀ = α

k₁ = hf(t_i, w_i)

k₂ = hf(t_i+[math]\displaystyle{ \tfrac{h}{4} }[/math], w_i+[math]\displaystyle{ \tfrac{k_1}{4} }[/math])

k₃ = hf(t_i+[math]\displaystyle{ \tfrac{3h}{8} }[/math], w_i+[math]\displaystyle{ \tfrac{3}{32} }[/math]k₁+[math]\displaystyle{ \tfrac{9}{32} }[/math]k₂)

k₄ = hf(t_i+[math]\displaystyle{ \tfrac{12h}{13} }[/math], w_i+[math]\displaystyle{ \tfrac{1932}{2197} }[/math]k₁-[math]\displaystyle{ \tfrac{7200}{2197} }[/math]k₂+[math]\displaystyle{ \tfrac{7296}{2197} }[/math]k₃)

k₅ = hf(t_i+h w_i+[math]\displaystyle{ \tfrac{439}{216} }[/math]k₁-8k₂+[math]\displaystyle{ \tfrac{3680}{513} }[/math]k₃-[math]\displaystyle{ \tfrac{845}{4104} }[/math]k₄)

k₆ = hf(t_i+[math]\displaystyle{ \tfrac{h}{2} }[/math] w_i+[math]\displaystyle{ \tfrac{8}{27} }[/math]k₁-2k₂+[math]\displaystyle{ \tfrac{3544}{2565} }[/math]k₃-[math]\displaystyle{ \tfrac{1859}{4104} }[/math]k₄-[math]\displaystyle{ \tfrac{11}{40} }[/math]k₅)

w_i+1 = w_i+[math]\displaystyle{ \tfrac{25}{216} }[/math]k₁+[math]\displaystyle{ \tfrac{1408}{2565} }[/math]k₃-[math]\displaystyle{ \tfrac{2197}{4104} }[/math]k₄-[math]\displaystyle{ \tfrac{1}{5} }[/math]k₅)

w'_i+1 = w_i+[math]\displaystyle{ \tfrac{16}{135} }[/math]k₁+[math]\displaystyle{ \tfrac{6656}{12825} }[/math]k₁+[math]\displaystyle{ \tfrac{28561}{56430} }[/math]k₄-[math]\displaystyle{ \tfrac{9}{50} }[/math]k₅-[math]\displaystyle{ \tfrac{2}{55} }[/math]k₆)

R = [math]\displaystyle{ \tfrac{1}{h}| }[/math]w'_i+1-w_i+1|

δ = 0.84 * [math]\displaystyle{ \tfrac{\varepsilon}{R}^\tfrac{1}{4} }[/math]

if R≤ε keep w as the current step solution and move to the next step with step size δh

if R>ε recalculate the current step with step size δh The above method is for each individual state, and not for the system as a whole. The w is the equivalent of the probability of being in a particular state, where the subscript i represents the time based variation. This still has to be done for all the states in the system, which later on is represented by the subscript j (for each state).

Detailed Methodology

Generate an initial step size h from the available failure rates (1% of the smallest MTTF)

Use the RK45 method on all states simultaneously using the given h. (this means that each state must have its k1 value calculated/used together, then k2, then k3, etc).

If all calculations are within tolerance, keep results (RK4, so the w without the hat) and increase h to the smallest of the increases generated by the method. If some of the calculations are not within tolerance, decrease the step size to the smallest of the decreases generated by the method and recalculate with the new h. h should not be increased to more than double, so s should have a stipulation on it that forbids from that occurring. Be aware that s may become infinite if the difference between the RK4 and the RK5 is zero. This should be addressed as well with a catch of some sort to make s = 2 in that case. (So basically if s is calculated to be greater than 2 for any state, make it equal to 2 for that state).

Repeat steps 2 & 3 as necessary.

If there are multiple phases, then 1-4 needs to be done for each phase where the initial probability of being in a state is = the final value from the previous phase.

This methodology will provide the ability to give availability and unavailability metrics for the system, as well as point probabilities of being in a certain state. For the reliability metrics, the methodology differs in that each unavailable state is considered as a “sink”, or in other words all transitions from unavailable to available states are to be ignored. This could be calculated simultaneously with the availability using the same step sizes as generated there.

The two results that need to be stored are the time and the corresponding probability of being in the state for each state.