Temperature-Nonthermal (TNT)-Weibull Model
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.
|
Temperature-Nonthermal (TNT)-Weibull Model |
This example compares the results for the temperature-nonthermal life-stress relationship with a Weibull distribution.
Reference Case
Data is from Table 7.10 on page 300 in book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.
Data
Temperature and switching rate are the two stresses used in the accelerated life test for a type of 18-V compact electromagnetic relay. The cycles to failure are provided next.
| Number in Group | State F/S | Time to State | Temperature (F) | Switching Rate | Subset ID | Number in Group | State F/S | Time to State | Temperature (F) | Switching Rate | Subset ID |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | F | 47154 | 337.15 | 10 | 1 | 1 | F | 29672 | 398.15 | 10 | 3 |
| 1 | F | 51307 | 337.15 | 10 | 1 | 1 | F | 38586 | 398.15 | 10 | 3 |
| 1 | F | 86149 | 337.15 | 10 | 1 | 1 | F | 47570 | 398.15 | 10 | 3 |
| 1 | F | 89702 | 337.15 | 10 | 1 | 1 | F | 56979 | 398.15 | 10 | 3 |
| 1 | F | 90044 | 337.15 | 10 | 1 | 6 | S | 57600 | 398.15 | 10 | 3 |
| 1 | F | 129795 | 337.15 | 10 | 1 | 1 | F | 7151 | 398.15 | 30 | 4 |
| 1 | F | 218384 | 337.15 | 10 | 1 | 1 | F | 11966 | 398.15 | 30 | 4 |
| 1 | F | 223994 | 337.15 | 10 | 1 | 1 | F | 16772 | 398.15 | 30 | 4 |
| 1 | F | 227383 | 337.15 | 10 | 1 | 1 | F | 17691 | 398.15 | 30 | 4 |
| 1 | F | 229354 | 337.15 | 10 | 1 | 1 | F | 18088 | 398.15 | 30 | 4 |
| 1 | F | 244685 | 337.15 | 10 | 1 | 1 | F | 18446 | 398.15 | 30 | 4 |
| 1 | F | 253690 | 337.15 | 10 | 1 | 1 | F | 19442 | 398.15 | 30 | 4 |
| 1 | F | 270150 | 337.15 | 10 | 1 | 1 | F | 25952 | 398.15 | 30 | 4 |
| 1 | F | 281499 | 337.15 | 10 | 1 | 1 | F | 29154 | 398.15 | 30 | 4 |
| 59 | S | 288000 | 337.15 | 10 | 1 | 1 | F | 30236 | 398.15 | 30 | 4 |
| 1 | F | 45663 | 337.15 | 30 | 2 | 1 | F | 33433 | 398.15 | 30 | 4 |
| 1 | F | 123237 | 337.15 | 30 | 2 | 1 | F | 33492 | 398.15 | 30 | 4 |
| 1 | F | 192073 | 337.15 | 30 | 2 | 1 | F | 39094 | 398.15 | 30 | 4 |
| 1 | F | 212696 | 337.15 | 30 | 2 | 1 | F | 51761 | 398.15 | 30 | 4 |
| 1 | F | 304669 | 337.15 | 30 | 2 | 1 | F | 53926 | 398.15 | 30 | 4 |
| 1 | F | 323332 | 337.15 | 30 | 2 | 1 | F | 57124 | 398.15 | 30 | 4 |
| 1 | F | 346814 | 337.15 | 30 | 2 | 1 | F | 61833 | 398.15 | 30 | 4 |
| 1 | F | 452855 | 337.15 | 30 | 2 | 1 | F | 67618 | 398.15 | 30 | 4 |
| 1 | F | 480915 | 337.15 | 30 | 2 | 1 | F | 70177 | 398.15 | 30 | 4 |
| 1 | F | 496672 | 337.15 | 30 | 2 | 1 | F | 71534 | 398.15 | 30 | 4 |
| 1 | F | 557136 | 337.15 | 30 | 2 | 1 | F | 79047 | 398.15 | 30 | 4 |
| 1 | F | 570003 | 337.15 | 30 | 2 | 1 | F | 91295 | 398.15 | 30 | 4 |
| 1 | F | 12019 | 398.15 | 10 | 3 | 1 | F | 92005 | 398.15 | 30 | 4 |
| 1 | F | 18590 | 398.15 | 10 | 3 |
Result
The following temperature non-thermal life stress relationship is used:
- [math]\displaystyle{ \,\!L\left ( f,T \right )=Af^{B}e^{\left ( \frac{E_{a}}{kT} \right )} }[/math]
where [math]\displaystyle{ \,\!f }[/math] is the switching rate, [math]\displaystyle{ \,\!T }[/math] is temperature. [math]\displaystyle{ \,\!L\left ( f,T \right ) }[/math] is the life characteristic affected by the two stresses. In ALTA, this life-stress relationship is called the "temperature non-thermal" model. This relationship also can be expressed as the following:
- [math]\displaystyle{ \,\!ln\left ( L\left ( x_{1},x_{2} \right ) \right )=\alpha _{0}+\alpha _{1}x_{1}+\alpha _{2}x_{2} }[/math]
where [math]\displaystyle{ \,\!x_{1}=\frac{1}{T} }[/math] and [math]\displaystyle{ \,\!x_{2}=ln\left ( f \right ) }[/math] .
The failure time distribution is a Weibull distribution. The book has the following results:
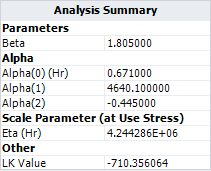
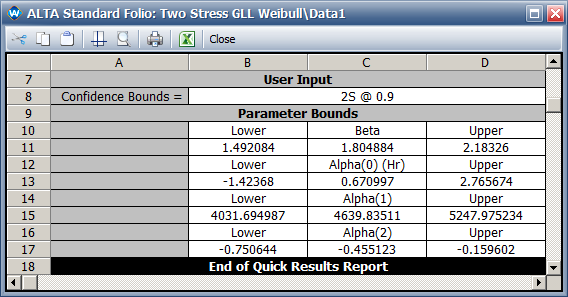
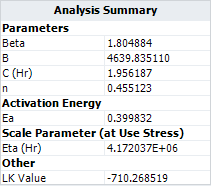
- The maximum likelihood estimation (MLE) results for the parameters are: [math]\displaystyle{ \,\!\alpha _{0}=0.671 }[/math] , [math]\displaystyle{ \,\!\alpha _{1}=4640.1 }[/math] , [math]\displaystyle{ \,\!\alpha _{2}=-0.445 }[/math] and [math]\displaystyle{ \,\!\beta =1.805 }[/math].
- The eta parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as [math]\displaystyle{ \,\!4.244\times 10^{6} }[/math].
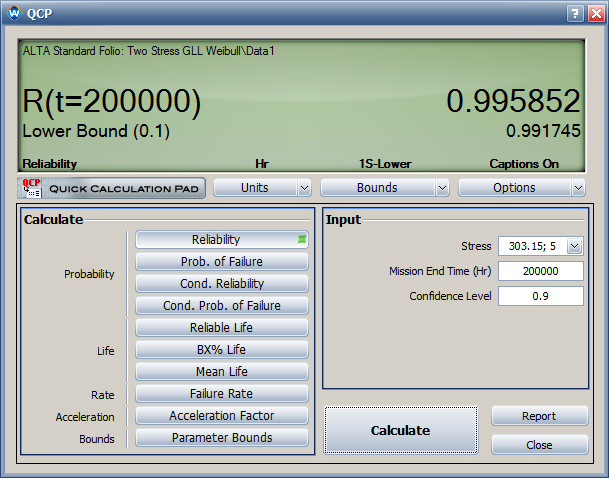
- The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992.
- The two-sided 90% confidence interval for parameter [math]\displaystyle{ \,\!\alpha _{2} }[/math] is [-0.751, -0.160].
Results in ALTA
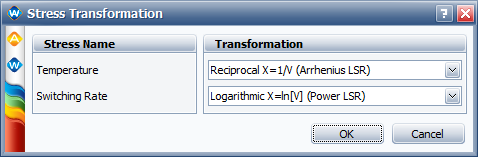
In ALTA, the General log linear model can be used. To have the same life-stress relation as the one in the book, the following transformation should be used for each stress:
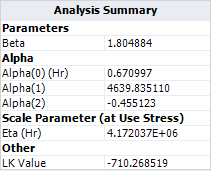
- The maximum likelihood estimation (MLE) results for the parameters are:
- These results (especially [math]\displaystyle{ \,\!\alpha _{2} }[/math]) are slightly different from the one given in the book. If we use the results in the book, then the calculated log likelihood value is -710.354601 as given below.
- This likelihood value is slightly smaller than the value given in ALTA, which is -710.268519. Therefore, the result in ALTA is better in terms of maximizing the log likelihood value.
- The η parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as [math]\displaystyle{ \,\!4.172\times 10^{6} }[/math] .
- The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 F) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992.
- The two-sided 90% confidence interval for parameter [math]\displaystyle{ \,\!\alpha _{2} }[/math] is [-0.751, -0.160].
If the temperature-Nonthermal relationship is used directly, the same results will be obtained. The following is the estimated model parameters for the temperature-nonthermal model in ALTA. By doing the right transformations for the stresses, a general log-linear model can become a temperature-nonthermal model.