General Log-Linear (GLL)-Weibull Model
From ReliaWiki
Revision as of 15:24, 13 June 2014 by Beth Ann Paape (talk | contribs)
ALTA_Reference_Examples_Banner.png
|
ALTA_Reference_Examples |
This example compares the results for the GLL life-stress relationship with a Weibull distribution.
Reference Case
The data set is from Example 7.14 on page 297 in book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.
Data
The following table shows the data.
| State F/S | Time to State (Hr) | Temperature (°C) | Group ID |
|---|---|---|---|
| F | 1138 | 100 | 1 |
| F | 1944 | 100 | 1 |
| F | 2764 | 100 | 1 |
| F | 2846 | 100 | 1 |
| F | 3246 | 100 | 1 |
| F | 3803 | 100 | 1 |
| F | 5046 | 100 | 1 |
| F | 5139 | 100 | 1 |
| S | 5500 | 100 | 1 |
| S | 5500 | 100 | 1 |
| S | 5500 | 100 | 1 |
| S | 5500 | 100 | 1 |
| F | 1121 | 120 | 2 |
| F | 1572 | 120 | 2 |
| F | 2329 | 120 | 2 |
| F | 2573 | 120 | 2 |
| F | 2702 | 120 | 2 |
| F | 3702 | 120 | 2 |
| F | 4277 | 120 | 2 |
| S | 4500 | 120 | 2 |
| F | 420 | 150 | 3 |
| F | 650 | 150 | 3 |
| F | 703 | 150 | 3 |
| F | 838 | 150 | 3 |
| F | 1086 | 150 | 3 |
| F | 1125 | 150 | 3 |
| F | 1387 | 150 | 3 |
| F | 1673 | 150 | 3 |
| F | 1896 | 150 | 3 |
| F | 2037 | 150 | 3 |
Result
The model used in the book is:
- [math]\displaystyle{ \,\!ln\left ( \eta \right )=\alpha _{0}+\alpha _{1}\frac{1}{T} }[/math]
The book has the following results:
- The model parameters are: [math]\displaystyle{ \,\!\alpha _{0}=-3.156 }[/math] , [math]\displaystyle{ \,\!\alpha _{1}=4390 }[/math] and [math]\displaystyle{ \,\!\beta =2.27 }[/math].
- The variance of each parameter is: [math]\displaystyle{ \,\!Var\left ( \alpha _{0} \right )=3.08 }[/math] , [math]\displaystyle{ \,\!Var\left ( \alpha _{1} \right )=484819.5 }[/math] and [math]\displaystyle{ \,\!Var\left ( \beta\right )=0.1396 }[/math] .
- The two-sided 90% confidence intervals for the model parameters are: [math]\displaystyle{ \,\!\left [ \alpha _{0,L},\alpha _{0,U} \right ]=\left [ -6.044, -0.269 \right ] }[/math] , [math]\displaystyle{ \,\!\left [ \alpha _{1,L},\alpha _{1,U} \right ]=\left [ 3244.8, 5535.3 \right ] }[/math] and [math]\displaystyle{ \,\!\left [ \beta _{1,L},\beta _{1,U} \right ]=\left [ 1.73, 2.97 \right ] }[/math] .
- The estimated B10 life at temperature of 35°C is 24,286 hours. The two-sided 90% confidence interval is [10371, 56867].
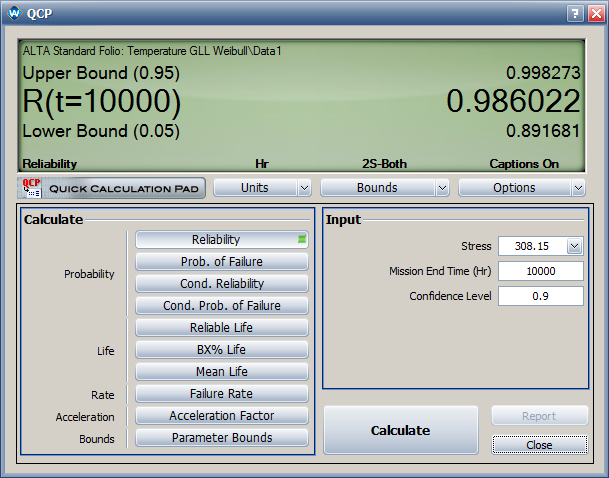
- The estimated reliability at 35°C and 10,000 hours is [math]\displaystyle{ \,\!R\left ( 10000 \right )=0.9860 }[/math] . The two-sided 90% confidence interval is [0.892, 0.998].
Results in ALTA
In ALTA, the GLL model with Weibull distribution is used. Since temperature is the stress, the reciprocal transform is used. The results are:
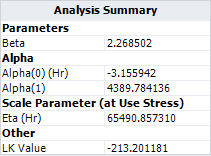
- The model parameters are:
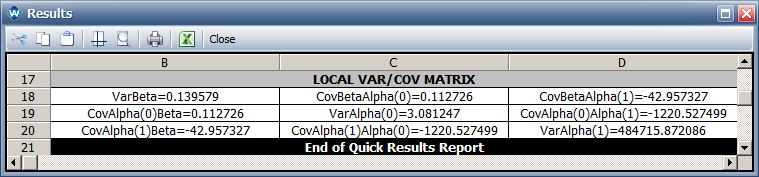
- The variances of the parameters are:
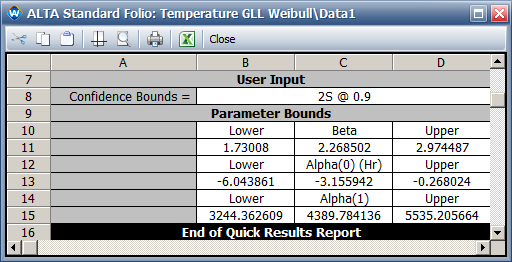
- The two-sided 90% confidence intervals for the model parameters are:
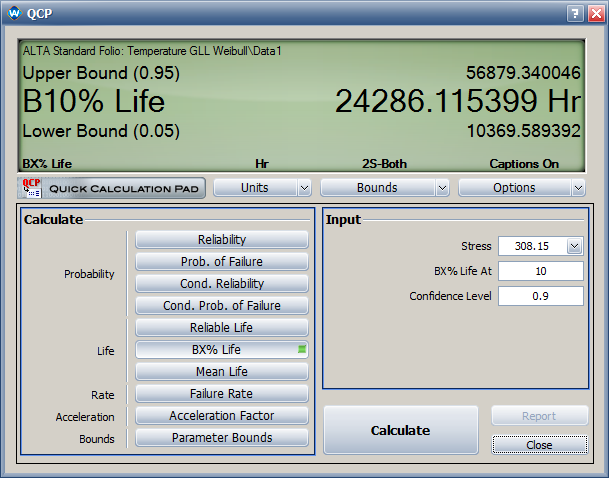
- The estimated B10 life and its two-sided 90% confidence intervals are:
- The estimated reliability with its two-sided 90% confidence interval at 35°C and 10,000 hours are: