Norris-Landzberg-Exponential Model
ALTA_Reference_Examples_Banner.png
|
ALTA_Reference_Examples |
Validate calculation of Norris-Landzberg relationship (can be done using the GLL model in ALTA with proper transformation for each stress).
Reference Case
Data is from Example 7.2 on page 257 in book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.
Data
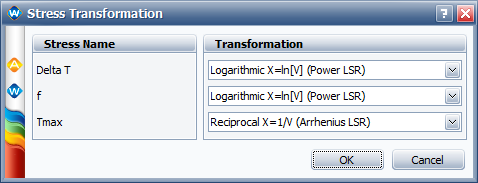
The thermal cycling profiles and test results for chip-scale package solder joints are given below. A thermal cycling profile can be represented by 3 independent stresses in Norris-Landzberg relationship. They are the maximum temperature , the temperature difference , and cycling frequency .
| Failure Time | T Max (°C) | Delta T(°C) | f |
|---|---|---|---|
| 208 | 80 | 120 | 1 |
| 225 | 80 | 120 | 2 |
| 308 | 80 | 120 | 3 |
| 142 | 100 | 140 | 2 |
| 108 | 120 | 160 | 2 |
| 169 | 100 | 120 | 2 |
| 131 | 120 | 120 | 2 |
| 1300 | 80 | 50 | 2 |
| 650 | 100 | 70 | 2 |
| 258 | 120 | 90 | 2 |
| 6231 | 30 | 50 | 2 |
| 1450 | 30 | 70 | 2 |
Result
For this data set, a multiple linear regression model is used in the book. The model parameters are estimated using the least squared estimation. The regression model is
- [math]\displaystyle{ \begin{align} eq\\ =&ln\left ( L \right )=\alpha _{0}+\alpha _{1}ln\left ( \Delta T \right )+\alpha _{3}ln\left ( \frac{1}{T_{MAX}} \right ) \end{align}\,\! }[/math]
Results in ALTA
In ALTA, the General Log-linear model is used with the proper transformation for each stress. The failure time distribution is Exponential.
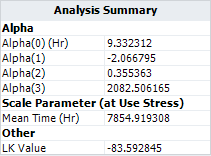
In ALTA, the maximum likelihood estimation is used. Therefore, the estimated model parameters are not exactly the same as the one given in the book where least squares method is used. The model result in ATLA is
The above results are close to what the book has.