New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
|
Lognormal MLE Solution with Right Censored Data
|
This example validates the calculations for the Lognormal MLE solution with Fisher matrix bound for right censored data in Weibull++ standard folios.
Reference Case
The data set on page 199 of the book Statistical Methods for Reliability Data by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998 is used.
Data
| Number in State
|
State F or S
|
Time to Failure
|
| 1 |
F |
252
|
| 1 |
F |
315
|
| 1 |
F |
369
|
| 1 |
F |
403
|
| 1 |
F |
474
|
| 15 |
S |
500
|
Result
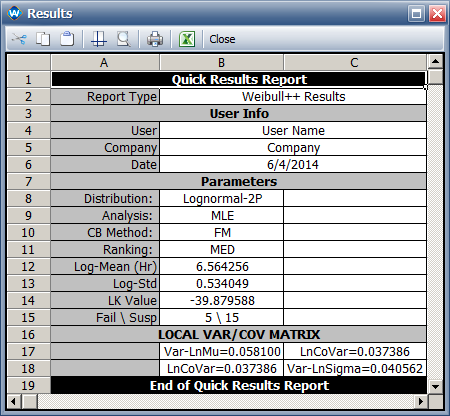
- The MLE solution is [math]\displaystyle{ \hat{\mu} = 6.56, \ \hat{\sigma} = 0.543\,\! }[/math].
- The variance and covariance matrix is
- [math]\displaystyle{
\sum =\begin{bmatrix}
0.0581 & 0.0374 \\
0.0374 & 0.0405
\end{bmatrix}\,\! }[/math]
Results in Weibull++
- The following picture shows the MLE solution and the variance/covariance matrix:
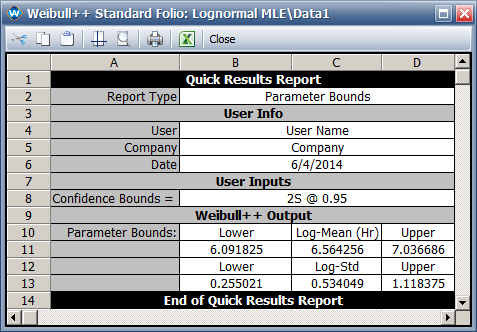
- The Fisher matrix bound for parameters are:
- For Ln-mu (using normal approximation of Eqn. 8.7 on page 187):
- [math]\displaystyle{ [\hat{\mu}'_{L}, \hat{\mu}'_{U}] = \hat{\mu}' \pm z_{(1-\alpha / 2)}se_{\hat{\mu}'}\,\! }[/math]
- For a confidence level of 0.95, it is:
- [math]\displaystyle{ \begin{alignat}{2}
[\hat{\mu}'_{L}, \hat{\mu}'_{U}] =& \hat{\mu}' \pm z_{(1-\alpha /2)}se_{\hat{\mu}'}\\
=& 6.564256 \pm 1.96 \times (0.0581)^{0.5}\\
=& [6.0918, 7.0366933]\\
\end{alignat}\,\! }[/math]
- For Ln-Std (using log-normal approximation of Eqn. 8.8 on page 188):
- [math]\displaystyle{ [\hat{\sigma}'_{L}, \hat{\sigma}'_{U}] = \hat{\sigma}'exp (\pm \frac{z_{(1-\alpha /2)}se_{\hat{\sigma}'}}{\hat{\sigma}'})\,\! }[/math]
- For confidence level of 0.95, it is:
- [math]\displaystyle{ \begin{alignat}{2}
[\hat{\sigma}'_{L}, \hat{\sigma}'_{U}] =& \hat{\sigma}'exp (\pm \frac{z_{(1-\alpha /2)}se_{\hat{\sigma}'}}{\hat{\sigma}'})\\
=& 0.534049 \times exp(\pm \tfrac{1.96\times 0.040562^{0.5}}{0.534049})\\
=& [0.255, 1.118]\\
\end{alignat} \,\! }[/math]
- The following picture shows the results in Weibull++: