Weibull-Bayesian with Prior Information on Beta
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
|
Weibull-Bayesian with Prior Information on Beta |
This example compares the Weibull-Bayesian calculation.
Reference Case
The data from Example 14.1 on page 348 in the book Statistical Methods for Reliability Data by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998 is used.
Data
| Number in State | State F or S | Time to Failure |
|---|---|---|
| 288 | S | 50 |
| 148 | S | 150 |
| 1 | F | 230 |
| 124 | S | 250 |
| 1 | F | 334 |
| 111 | S | 350 |
| 1 | F | 423 |
| 106 | S | 450 |
| 99 | S | 550 |
| 110 | S | 650 |
| 114 | S | 750 |
| 119 | S | 850 |
| 127 | S | 950 |
| 1 | F | 990 |
| 1 | F | 1009 |
| 123 | S | 1050 |
| 93 | S | 1150 |
| 47 | S | 1250 |
| 41 | S | 1350 |
| 27 | S | 1450 |
| 1 | F | 1510 |
| 11 | S | 1550 |
| 6 | S | 1650 |
| 1 | S | 1850 |
| 2 | S | 2050 |
Result
In the book, the prior distribution is set for [math]\displaystyle{ \sigma\,\! }[/math] with [math]\displaystyle{ \sigma = \frac{1}{\beta}\,\! }[/math]. The prior for [math]\displaystyle{ \sigma\,\! }[/math] is a lognormal distribution specified by [math]\displaystyle{ \sigma_{0.005}\,\! }[/math] = 0.2 and [math]\displaystyle{ \sigma_{0.995}\,\! }[/math] = 0.5. The following results are obtained using the Bayesian method:
- The 95% two-sided Bayesian confidence interval for [math]\displaystyle{ t_{0.05}\,\! }[/math] (B5% life) is [1613, 3236]. This result is given in Example 14.7 on page 357.
- The 95% two-sided Bayesian confidence interval for [math]\displaystyle{ t_{0.10}\,\! }[/math] (B10% life) is [2018, 4400]. This result is given in Example 14.7 on page 357.
- The 95% two-sided Bayesian confidence interval for F(2000) (probability of failure at time of 2000) is [0.015, 0.097]. This result is given in Example 14.8 on page 357.
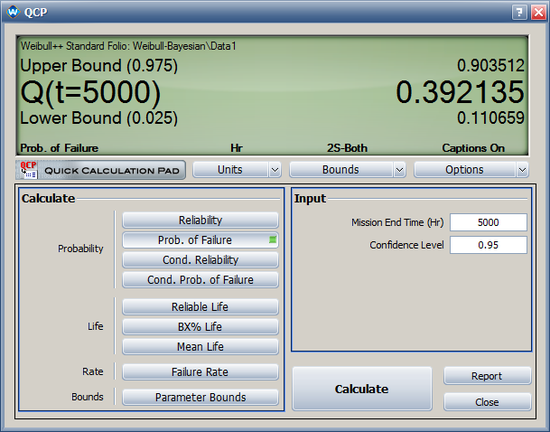
- The 95% two-sided Bayesian confidence interval for F(5000) (probability of failure at time of 5000) is [0.132, 0.905]. This result is given in Example 14.8 on page 357.
Results in Weibull++
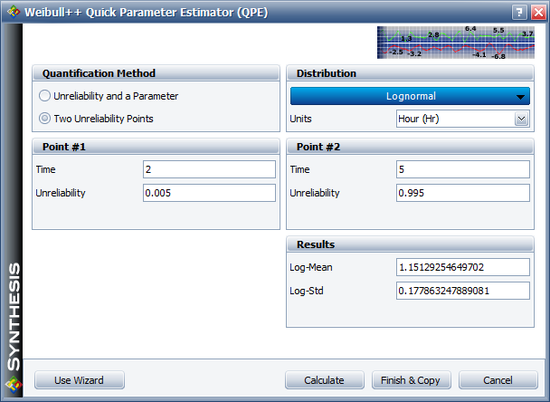
In Weibull++, the prior distribution is set for [math]\displaystyle{ \beta\,\! }[/math] directly. Based on the information of [math]\displaystyle{ \sigma\,\! }[/math], we know [math]\displaystyle{ \beta_{0.005}\,\! }[/math] = 2 and [math]\displaystyle{ \beta_{0.995}\,\! }[/math] = 5. Therefore, we can get the prior lognormal distribution for [math]\displaystyle{ \beta\,\! }[/math]. It is Log-Mean = 1.15129 and Log-Std = 0.17786.
Applying this prior distribution for Wei-Bayesian, we have the following results:
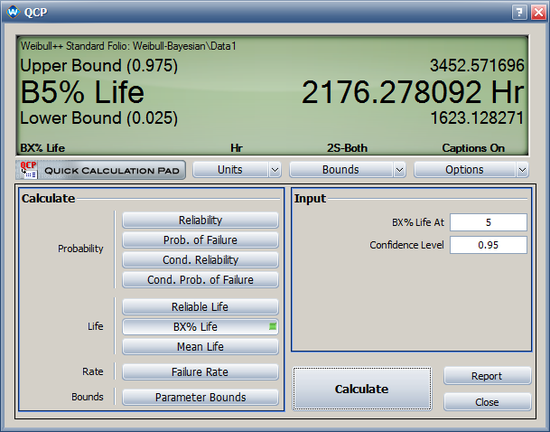
- The 95% two-sided Bayesian confidence interval for [math]\displaystyle{ t_{0.05}\,\! }[/math] (B5% life) is [1623, 3452].
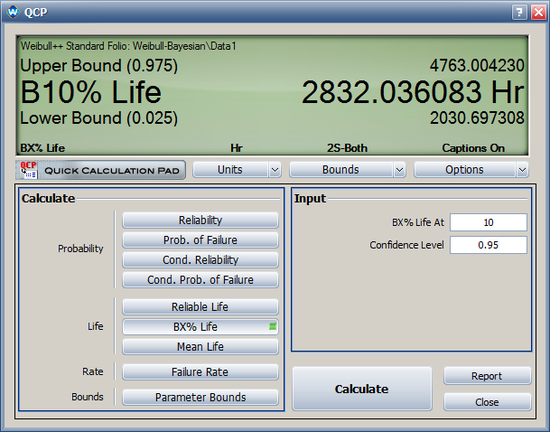
- The 95% two-sided Bayesian confidence interval for [math]\displaystyle{ t_{0.10}\,\! }[/math] (B10% life) is [2030, 4763].
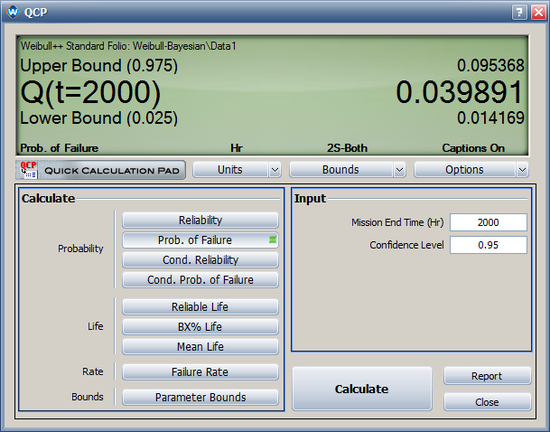
- The 95% two-sided Bayesian confidence interval for F(2000) (probability of failure at time of 2000) is [0.014, 0.095].
- The 95% two-sided Bayesian confidence interval for F(5000) (probability of failure at time of 5000) is [0.111, 0.903].
The results in Weibull++ are very close, but not exactly the same, as the results in the book. The differences are mainly caused by the fact that the prior lognormal distribution is for [math]\displaystyle{ \sigma\,\! }[/math] in the book while it is for [math]\displaystyle{ \beta\,\! }[/math] in Weibull++.