Temperature-NonThermal Relationship

Temperature-NonThermal Relationship

Introduction

When temperature and a second non-thermal stress (e.g. voltage) are the accelerated stresses of a test, then the Arrhenius and the inverse power law relationships can be combined to yield the Temperature-NonThermal (T-NT) relationship. This relationship is given by:

[math]\displaystyle{ L(U,V)=\frac{C}{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}} }[/math]

where:
• [math]\displaystyle{ U }[/math] is the non-thermal stress (i.e., voltage, vibration, etc.)
• [math]\displaystyle{ V }[/math] is the temperature (in absolute units ).

[math]\displaystyle{ B, }[/math] [math]\displaystyle{ C, }[/math] [math]\displaystyle{ n }[/math] are the parameters to be determined.

The T-NT relationship can be linearized and plotted on a Life vs. Stress plot. The relationship is linearized by taking the natural logarithm of both sides in Eqn. (Temp-Volt) or:

[math]\displaystyle{ \ln (L(V,U))=\ln (C)-n\ln (U)+\frac{B}{V} }[/math]

Since life is now a function of two stresses, a Life vs. Stress plot can only be obtained by keeping one of the two stresses constant and varying the other one. Doing so will yield the straight line described by Eqn. (ln Temp-Volt), where the term for the stress which is kept at a fixed value becomes another constant (in addition to the [math]\displaystyle{ \ln (C) }[/math] constant). When the non-thermal stress is kept constant, then Eqn. (ln Temp-Volt) becomes:

[math]\displaystyle{ \ln (L(V))=const.+\frac{B}{V} }[/math]

This is the Arrhenius equation and it is plotted on a log-reciprocal scale. When the thermal stress is kept constant, then Eqn. (ln Temp-Volt) becomes:

[math]\displaystyle{ \ln (L(U))=const.-n\ln (U) }[/math]

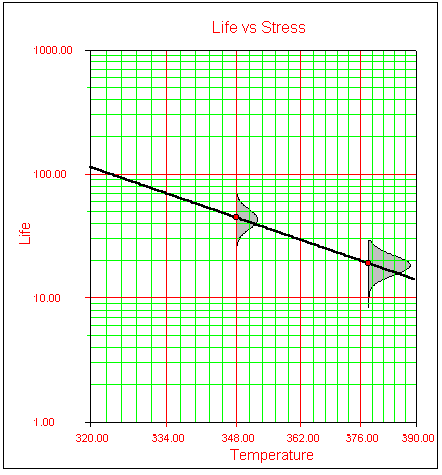
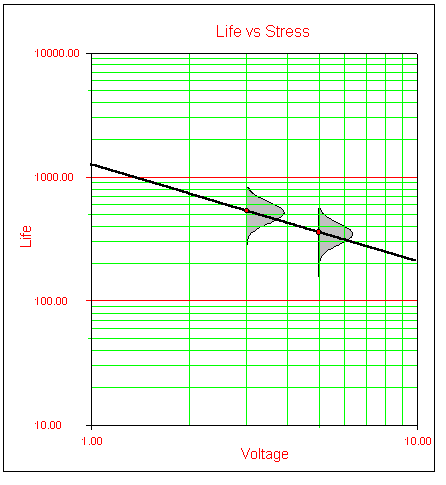
This is the inverse power law equation and it is plotted on a log-log scale. In Figs. 1 and 2, data obtained from a temperature and voltage test were analyzed and plotted on a log-reciprocal scale. In Fig. 1, life is plotted versus temperature, with voltage held at a fixed value. In Fig. 2, life is plotted versus voltage, with temperature held at a fixed value.

[math]\displaystyle{ R=459.67+{}^\circ F. }[/math]

Fig. 1: Life vs. Temperature (Arrhenius plot) at a fixed voltage level.

Fig. 2: Life vs. Voltage plot at a fixed temperature level.

A look at the Parameters [math]\displaystyle{ B }[/math] and [math]\displaystyle{ n }[/math]

Depending on which stress type is kept constant, it can be seen from Eqns. (ln Temp) and (ln Hum) that either the parameter [math]\displaystyle{ B }[/math] or the parameter [math]\displaystyle{ n }[/math] is the slope of the resulting line. If, for example, the non-thermal stress is kept constant (Fig. 1) then [math]\displaystyle{ B }[/math] is the slope of the life line in a Life vs. Temperature plot. The steeper the slope, the greater the dependency of the product's life to the temperature. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that temperature has on the life and [math]\displaystyle{ n }[/math] is a measure of the effect that the non-thermal stress has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the temperature. Similarly, the larger the value of [math]\displaystyle{ n, }[/math] the higher the dependency of the life on the non-thermal stress.

Acceleration Factor

The acceleration factor for the T-NT relationship is given by:

[math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{C}{U_{u}^{n}}{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\tfrac{C}{U_{A}^{n}}{{e}^{\tfrac{B}{{{V}_{A}}}}}}={{\left( \frac{{{U}_{A}}}{{{U}_{u}}} \right)}^{n}}{{e}^{B\left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)}} }[/math]

where:
• [math]\displaystyle{ {{L}_{USE}} }[/math] is the life at use stress level.
• [math]\displaystyle{ {{L}_{Accelerated}} }[/math] is the life at the accelerated stress level.
• [math]\displaystyle{ {{V}_{u}} }[/math] is the use temperature level.
• [math]\displaystyle{ {{V}_{A}} }[/math] is the accelerated temperature level.
• [math]\displaystyle{ {{U}_{A}} }[/math] is the accelerated non-thermal level.
• [math]\displaystyle{ {{U}_{u}} }[/math] is the use non-thermal level.
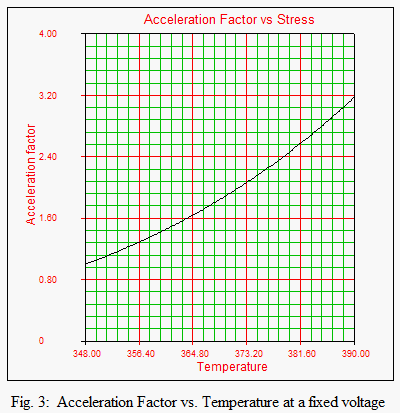
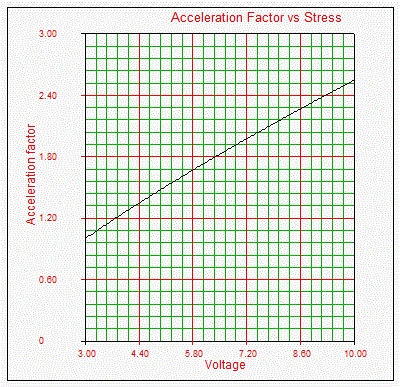
The acceleration factor is plotted versus stress in the same manner used to create the Life vs. Stress plots. That is, one stress type is kept constant and the other is varied (see Figs. 3 and 4).

[math]\displaystyle{ \begin{align} & \overline{T}= & \int\limits_{0}^{\infty }t\cdot f(t,U,V)dt \\ & = & \int\limits_{0}^{\infty }t\cdot \frac{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}{{e}^{-\tfrac{t\cdot {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}}}dt \\ & = & \frac{C}{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}} \end{align} }[/math]

Fig. 3: Acceleration Factor vs. Temperature at a fixed voltage level.

Fig. 4: Acceleration Factor vs. Voltage at a fixed temperature level.

T-NT Exponential

By setting [math]\displaystyle{ m=L(U,V) }[/math] as given in Eqn. (Temp-Volt), the exponential [math]\displaystyle{ pdf }[/math] becomes:

[math]\displaystyle{ f(t,U,V)=\frac{{{U}^{n}}}{C}{{e}^{-\tfrac{B}{V}}}\cdot {{e}^{-\tfrac{{{U}^{n}}}{C}\left( {{e}^{-\tfrac{B}{V}}} \right)t}} }[/math]

T-NT Exponential Statistical Properties Summary

Mean or MTTF

The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) for the T-NT exponential model is given by:

[math]\displaystyle{ \begin{align} & \overline{T}= & \int\limits_{0}^{\infty }t\cdot f(t,U,V)dt \\ & = & \int\limits_{0}^{\infty }t\cdot \frac{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}{{e}^{-\tfrac{t\cdot {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}}}dt \\ & = & \frac{C}{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}} \end{align} }[/math]

Median

The median, [math]\displaystyle{ \breve{T}, }[/math] for the T-NT exponential model is given by:

[math]\displaystyle{ \breve{T}=\frac{1}{\lambda }0.693=0.693\frac{C}{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}} }[/math]

Mode

The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the T-NT exponential model is given by:

[math]\displaystyle{ \tilde{T}=0 }[/math]

Standard Deviation

The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math] , for the T-NT exponential model is given by:

[math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{\lambda }=m=\frac{C}{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}} }[/math]

T-NT Exponential Reliability Function

The T-NT exponential reliability function is given by:

[math]\displaystyle{ R(T,U,V)={{e}^{-\tfrac{T\cdot {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}}} }[/math]

This function is the complement of the T-NT exponential cumulative distribution function or:

[math]\displaystyle{ R(T,U,V)=1-Q(T,U,V)=1-\mathop{}_{0}^{T}f(T)dT }[/math]

and,

[math]\displaystyle{ R(T,U,V)=1-\mathop{}_{0}^{T}\frac{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}{{e}^{-\tfrac{T\cdot {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}}}dT={{e}^{-\tfrac{T\cdot {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}}} }[/math]

Conditional Reliability

The conditional reliability function for the T-NT exponential model is given by,

[math]\displaystyle{ R(T,t,U,V)=\frac{R(T+t,U,V)}{R(T,U,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\tfrac{t\cdot {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}}} }[/math]

Reliable Life

For the T-NT exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}} }[/math] , is given by:

[math]\displaystyle{ R({{t}_{R}},U,V)={{e}^{-\tfrac{{{t}_{R}}\cdot {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}}} }[/math]

[math]\displaystyle{ \ln [R({{t}_{R}},U,V)]{{=}^{-\tfrac{{{t}_{R}}\cdot {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}}} }[/math]

or:

[math]\displaystyle{ {{t}_{R}}=-\frac{C}{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}\ln [R({{t}_{R}},U,V)] }[/math]

Parameter Estimation

Maximum Likelihood Estimation Method

Substituting the T-NT relationship into the exponential log-likelihood equation yields:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{U_{i}^{n}}{C}{{e}^{-\tfrac{B}{{{V}_{i}}}}}\cdot {{e}^{-\tfrac{U_{i}^{n}}{C}\left( {{e}^{-\tfrac{B}{{{V}_{i}}}}} \right){{T}_{i}}}} \right] \\ & & -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{U_{i}^{n}}{C}\left( {{e}^{-\tfrac{B}{{{V}_{i}}}}} \right)T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\tfrac{T_{Li}^{\prime \prime }}{C}U_{i}^{\prime \prime n}{{e}^{-\tfrac{B}{{{V}_{i}}}}}}} }[/math]

[math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\tfrac{T_{Ri}^{\prime \prime }}{C}U_{i}^{\prime \prime n}{{e}^{-\tfrac{B}{{{V}_{i}}}}}}} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure data points in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ B }[/math] is the T-NT parameter (unknown, the first of three parameters to be estimated).
• [math]\displaystyle{ C }[/math] is the second T-NT parameter (unknown, the second of three parameters to be estimated).
• [math]\displaystyle{ n }[/math] is the third T-NT parameter (unknown, the third of three parameters to be estimated).
• [math]\displaystyle{ {{V}_{i}} }[/math] is the temperature level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{U}_{i}} }[/math] is the non-thermal stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the i [math]\displaystyle{ ^{th} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the i [math]\displaystyle{ ^{th} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the i [math]\displaystyle{ ^{th} }[/math] interval.

The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ B, }[/math] [math]\displaystyle{ C }[/math] and [math]\displaystyle{ n }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0, }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial C}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial n}=0 }[/math] .

T-NT Weibull

By setting [math]\displaystyle{ \eta =L(U,V) }[/math] from Eqn. (Temp-Volt), the T-NT Weibull model is given by:

[math]\displaystyle{ f(t,U,V)=\frac{\beta {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}{{\left( \frac{t\cdot {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t\cdot {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C} \right)}^{\beta }}}} }[/math]

T-NT Weibull Statistical Properties Summary

Mean or MTTF

The mean, [math]\displaystyle{ \overline{T} }[/math] , for the T-NT Weibull model is given by:

[math]\displaystyle{ \overline{T}=\frac{C}{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right) }[/math]

where [math]\displaystyle{ \Gamma \left( \tfrac{1}{\beta }+1 \right) }[/math] is the gamma function evaluated at the value of [math]\displaystyle{ \left( \tfrac{1}{\beta }+1 \right) }[/math] .

Median

The median, [math]\displaystyle{ \breve{T}, }[/math] for the T-NT Weibull model is given by:

[math]\displaystyle{ \breve{T}=\frac{C}{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{{\left( \ln 2 \right)}^{\tfrac{1}{\beta }}} }[/math]

Mode

The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the T-NT Weibull model is given by:

[math]\displaystyle{ \tilde{T}=\frac{C}{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{{\left( 1-\frac{1}{\beta } \right)}^{\tfrac{1}{\beta }}} }[/math]

Standard Deviation

The standard deviation, [math]\displaystyle{ {{\sigma }_{T}}, }[/math] for the T-NT Weibull model is given by:

[math]\displaystyle{ {{\sigma }_{T}}=\frac{C}{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}\cdot \sqrt{\Gamma \left( \frac{2}{\beta }+1 \right)-{{\left( \Gamma \left( \frac{1}{\beta }+1 \right) \right)}^{2}}} }[/math]

T-NT Weibull Reliability Function

The T-NT Weibull reliability function is given by:

[math]\displaystyle{ R(T,U,V)={{e}^{-{{\left( \tfrac{T{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C} \right)}^{\beta }}}} }[/math]

Conditional Reliability Function

The T-NT Weibull conditional reliability function at a specified stress level is given by:

[math]\displaystyle{ R(T,t,U,V)=\frac{R(T+t,U,V)}{R(T,U,V)}=\frac{{{e}^{-{{\left( \tfrac{\left( T+t \right){{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C} \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C} \right)}^{\beta }}}}} }[/math]

or:

[math]\displaystyle{ R(T,t,U,V)={{e}^{-\left[ {{\left( \tfrac{\left( T+t \right){{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C} \right)}^{\beta }}-{{\left( \tfrac{T{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C} \right)}^{\beta }} \right]}} }[/math]

Reliable Life

For the T-NT Weibull model, the reliable life, [math]\displaystyle{ {{T}_{R}} }[/math] , of a unit for a specified reliability and starting the mission at age zero is given by:

[math]\displaystyle{ {{T}_{R}}=\frac{C}{{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{{\left\{ -\ln \left[ R\left( {{T}_{R}},U,V \right) \right] \right\}}^{\tfrac{1}{\beta }}} }[/math]

T-NT Weibull Failure Rate Function

The T-NT Weibull failure rate function, [math]\displaystyle{ \lambda (T) }[/math] , is given by:

[math]\displaystyle{ \lambda \left( T,U,V \right)=\frac{f\left( T,U,V \right)}{R\left( T,U,V \right)}=\frac{\beta {{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C}{{\left( \frac{T{{U}^{n}}{{e}^{-\tfrac{B}{V}}}}{C} \right)}^{\beta -1}} }[/math]

Parameter Estimation

Maximum Likelihood Estimation Method

Substituting the T-NT relationship into the Weibull log-likelihood function yields:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{\beta U_{i}^{n}{{e}^{-\tfrac{B}{{{V}_{i}}}}}}{C}{{\left( \frac{U_{i}^{n}{{e}^{-\tfrac{B}{{{V}_{i}}}}}}{C}{{T}_{i}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{U_{i}^{n}{{e}^{-\tfrac{B}{{{V}_{i}}}}}}{C}{{T}_{i}} \right)}^{\beta }}}} \right] \\ & & -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( \frac{U_{i}^{n}{{e}^{-\tfrac{B}{{{V}_{i}}}}}}{C}T_{i}^{\prime } \right)}^{\beta }}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{C}U_{i}^{\prime \prime n}{{e}^{-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }}}} }[/math]

[math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{C}U_{i}^{\prime \prime n}{{e}^{-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }}}} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure data points in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ \beta }[/math] is the Weibull shape parameter (unknown, the first of four parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the first T-NT parameter (unknown, the second of four parameters to be estimated).
• [math]\displaystyle{ C }[/math] is the second T-NT parameter (unknown, the third of four parameters to be estimated).
• [math]\displaystyle{ n }[/math] is the third T-NT parameter (unknown, the fourth of four parameters to be estimated).
• [math]\displaystyle{ {{V}_{i}} }[/math] is the temperature level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{U}_{i}} }[/math] is the non-thermal stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
•
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} \lt br\gt • }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ B, }[/math] [math]\displaystyle{ C, }[/math] [math]\displaystyle{ n }[/math] and [math]\displaystyle{ \beta }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0, }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial C}=0, }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial n}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \beta }=0 }[/math] .

T-NT Lognormal

The [math]\displaystyle{ pdf }[/math] of the lognormal distribution is given by:

[math]\displaystyle{ f(T)=\frac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\overline{{{T}'}}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}} }[/math]

where:

[math]\displaystyle{ {T}'=\ln (T) }[/math]

and:
• [math]\displaystyle{ T= }[/math] times-to-failure.
• [math]\displaystyle{ \overline{{{T}'}}= }[/math] mean of the natural logarithms of the times-to-failure.
• [math]\displaystyle{ {{\sigma }_{{{T}'}}}= }[/math] standard deviation of the natural logarithms of the times-to-failure.
The median of the lognormal distribution is given by:

[math]\displaystyle{ \breve{T}={{e}^{{{\overline{T}}^{\prime }}}} }[/math]

The T-NT lognormal model [math]\displaystyle{ pdf }[/math] can be obtained first by setting [math]\displaystyle{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}=L(V) }[/math] in Eqn. (Temp-Volt).
Therefore:

[math]\displaystyle{ \breve{T}=L(V)=\frac{C}{{{U}^{n}}}{{e}^{\tfrac{B}{V}}} }[/math]

or:

[math]\displaystyle{ {{e}^{{{\overline{T}}^{\prime }}}}=\frac{C}{{{U}^{n}}}{{e}^{\tfrac{B}{V}}} }[/math]

Thus:

[math]\displaystyle{ {{\overline{T}}^{\prime }}=\ln (C)-n\ln (U)+\frac{B}{V} }[/math]

Substituting Eqn.(TV-logn-mean)into Eqn. (TV-logn-pdf) yields the T-NT lognormal model [math]\displaystyle{ pdf }[/math] or:

[math]\displaystyle{ f(T,U,V)=\frac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\ln (C)+n\ln (U)-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}} }[/math]

T-N-T Lognormal Statistical Properties Summary

The Mean

• The mean life of the T-NT lognormal model (mean of the times-to-failure), [math]\displaystyle{ \bar{T} }[/math] , is given by:

[math]\displaystyle{ \begin{align} & \bar{T}= & {{e}^{\bar{{T}'}+\tfrac{1}{2}\sigma _{{{T}'}}^{2}}} \\ & = & {{e}^{\ln (C)-n\ln (U)+\tfrac{B}{V}+\tfrac{1}{2}\sigma _{{{T}'}}^{2}}} \end{align} }[/math]

• The mean of the natural logarithms of the times-to-failure, [math]\displaystyle{ {{\bar{T}}^{^{\prime }}} }[/math] , in terms of [math]\displaystyle{ \bar{T} }[/math] and [math]\displaystyle{ {{\sigma }_{T}} }[/math] is given by:

[math]\displaystyle{ {{\bar{T}}^{\prime }}=\ln \left( {\bar{T}} \right)-\frac{1}{2}\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right) }[/math]

The Standard Deviation

• The standard deviation of the T-NT lognormal model (standard deviation of the times-to-failure), [math]\displaystyle{ {{\sigma }_{T}} }[/math] , is given by:

[math]\displaystyle{ \begin{align} & {{\sigma }_{T}}= & \sqrt{\left( {{e}^{2\bar{{T}'}+\sigma _{{{T}'}}^{2}}} \right)\left( {{e}^{\sigma _{{{T}'}}^{2}}}-1 \right)} \\ & = & \sqrt{\left( {{e}^{2\left( \ln (C)-n\ln (U)+\tfrac{B}{V} \right)+\sigma _{{{T}'}}^{2}}} \right)\left( {{e}^{\sigma _{{{T}'}}^{2}}}-1 \right)} \end{align} }[/math]

• The standard deviation of the natural logarithms of the times-to-failure, [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] , in terms of [math]\displaystyle{ \bar{T} }[/math] and [math]\displaystyle{ {{\sigma }_{T}} }[/math] is given by:
•
• [math]\displaystyle{ {{\sigma }_{{{T}'}}}=\sqrt{\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)} }[/math]
•
•

The Mode

• The mode of the T-NT lognormal model is given by:

[math]\displaystyle{ \begin{align} & \tilde{T}= & {{e}^{{{\overline{T}}^{\prime }}-\sigma _{{{T}'}}^{2}}} \\ & = & {{e}^{\ln (C)-n\ln (U)+\tfrac{B}{V}-\sigma _{{{T}'}}^{2}}} \end{align} }[/math]

T-NT Lognormal Reliability

For the T-NT lognormal model, the reliability for a mission of time [math]\displaystyle{ T }[/math] , starting at age 0, for the T-NT lognormal model is determined by:

[math]\displaystyle{ R(T,U,V)=\mathop{}_{T}^{\infty }f(t,U,V)dt }[/math]

or:

[math]\displaystyle{ R(T,U,V)=\mathop{}_{{{T}^{^{\prime }}}}^{\infty }\frac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t-\ln (C)+n\ln (U)-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}dt }[/math]

Reliable Life

For the T-NT lognormal model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}, }[/math] is estimated by first solving the reliability equation with respect to time, as follows:

[math]\displaystyle{ T_{R}^{\prime }=\ln (C)-n\ln (U)+\frac{B}{V}+z\cdot {{\sigma }_{{{T}'}}} }[/math]

where:

[math]\displaystyle{ z={{\Phi }^{-1}}\left[ F\left( T_{R}^{\prime },U,V \right) \right] }[/math]

and:

[math]\displaystyle{ \Phi (z)=\frac{1}{\sqrt{2\pi }}\mathop{}_{-\infty }^{z({T}',U,V)}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt }[/math]

Since [math]\displaystyle{ {T}'=\ln (T) }[/math] the reliable life, [math]\displaystyle{ {{t}_{R}} }[/math] , is given by:

[math]\displaystyle{ {{t}_{R}}={{e}^{T_{R}^{\prime }}} }[/math]

Lognormal Failure Rate

The T-NT lognormal failure rate is given by:

[math]\displaystyle{ \lambda (T,U,V)=\frac{f(T,U,V)}{R(T,U,V)}=\frac{\tfrac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\ln (C)+n\ln (U)-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}}{\mathop{}_{{{T}'}}^{\infty }\tfrac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\ln (C)+n\ln (U)-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}dt} }[/math]

Parameter Estimation

Maximum Likelihood Estimation Method

The complete T-NT lognormal log-likelihood function is:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{{{\sigma }_{{{T}'}}}{{T}_{i}}}{{\phi }_{pdf}}\left( \frac{\ln \left( {{T}_{i}} \right)-\ln (C)+n\ln ({{U}_{i}})-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right) \right] \\ & & \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ 1-\Phi \left( \frac{\ln \left( T_{i}^{\prime } \right)-\ln (C)+n\ln ({{U}_{i}})-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right) \right] \\ & & +\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]

where:

[math]\displaystyle{ z_{Ri}^{\prime \prime }=\frac{\ln T_{Ri}^{\prime \prime }-\ln C+n\ln U_{i}^{\prime \prime }-\tfrac{B}{{{V}_{i}}}}{\sigma _{T}^{\prime }} }[/math]

[math]\displaystyle{ z_{Li}^{\prime \prime }=\frac{\ln T_{Li}^{\prime \prime }-\ln C+n\ln U_{i}^{\prime \prime }-\tfrac{B}{{{V}_{i}}}}{\sigma _{T}^{\prime }} }[/math]

[math]\displaystyle{ \phi \left( x \right)=\frac{1}{\sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( x \right)}^{2}}}} }[/math]

[math]\displaystyle{ \Phi (x)=\frac{1}{\sqrt{2\pi }}\mathop{}_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure data points in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] is the standard deviation of the natural logarithm of the times-to-failure (unknown, the first of four parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the first T-NT parameter (unknown, the second of four parameters to be estimated).
• [math]\displaystyle{ C }[/math] is the second T-NT parameter (unknown, the third of four parameters to be estimated).
• [math]\displaystyle{ n }[/math] is the third T-NT parameter (unknown, the fourth of four parameters to be estimated).
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level for the first stress type (i.e. temperature) of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{U}_{i}} }[/math] is the stress level for the second stress type (i.e. non-thermal) of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

The solution (parameter estimates) will be found by solving for [math]\displaystyle{ {{\widehat{\sigma }}_{{{T}'}}}, }[/math] [math]\displaystyle{ \widehat{B}, }[/math] [math]\displaystyle{ \widehat{C}, }[/math] [math]\displaystyle{ \widehat{n} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}=0, }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0, }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial C}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial n}=0 }[/math] .

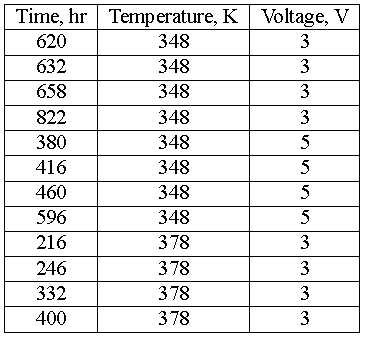
Example

Twelve electronic devices were put into a continuous accelerated test and the following data were collected.

Using ALTA and the T-NT lognormal model, the following parameters were obtained:

[math]\displaystyle{ \begin{align} & \widehat{Std}= & 0.1825579885 \\ & \widehat{B}= & 3729.6503028119 \\ & \widehat{C}= & 0.0352919977 \\ & \widehat{n}= & 0.7767966480 \end{align} }[/math]

A probability plot for the use stress levels of 323K and 2V is shown next.

File:ALTA10.5.gif

Fig. 5: Probability plot for the use stress levels of 323K and 2V.

File:ALTA10.6.gif

Fig. 6: Acceleration Factor versus temperature given a constant voltage of 2V.

An acceleration factor plot, in which one of the stresses must be kept constant, can also be obtained. For example, in the following plot, the acceleration factor is plotted versus temperature given a constant voltage of 2V, as shown next.

Appendix 10A: T-NT Confidence Bounds

Approximate Confidence Bounds for the T-NT Exponential

Confidence Bounds on the Mean Life

The mean life for the T-NT model is given by Eqn. (Temp-Volt) by setting [math]\displaystyle{ m=L(V) }[/math] . The upper [math]\displaystyle{ ({{m}_{U}}) }[/math] and lower [math]\displaystyle{ ({{m}_{L}}) }[/math] bounds on the mean life (ML estimate of the mean life) are estimated by:

[math]\displaystyle{ {{m}_{U}}=\widehat{m}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}} }[/math]

[math]\displaystyle{ {{m}_{L}}=\widehat{m}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}} }[/math]

where [math]\displaystyle{ {{K}_{\alpha }} }[/math] is defined by:

[math]\displaystyle{ \alpha =\frac{1}{\sqrt{2\pi }}\mathop{}_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }}) }[/math]

If [math]\displaystyle{ \delta }[/math] is the confidence level, then [math]\displaystyle{ \alpha =\tfrac{1-\delta }{2} }[/math] for the two-sided bounds, and [math]\displaystyle{ \alpha =1-\delta }[/math] for the one-sided bounds. The variance of [math]\displaystyle{ \widehat{m} }[/math] is given by:

[math]\displaystyle{ \begin{align} & Var(\widehat{m})= & {{\left( \frac{\partial m}{\partial B} \right)}^{2}}Var(\widehat{B})+{{\left( \frac{\partial m}{\partial C} \right)}^{2}}Var(\widehat{C}) \\ & & +{{\left( \frac{\partial m}{\partial n} \right)}^{2}}Var(\widehat{b}) \\ & & +2\left( \frac{\partial m}{\partial B} \right)\left( \frac{\partial m}{\partial C} \right)Cov(\widehat{B},\widehat{C}) \\ & & +2\left( \frac{\partial m}{\partial B} \right)\left( \frac{\partial m}{\partial n} \right)Cov(\widehat{B},\widehat{n}) \\ & & +2\left( \frac{\partial m}{\partial C} \right)\left( \frac{\partial m}{\partial n} \right)Cov(\widehat{C},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{m})= & \frac{1}{{{U}^{2\widehat{n}}}}{{e}^{2\tfrac{\widehat{B}}{V}}}[\frac{{{\widehat{C}}^{2}}}{{{V}^{2}}}Var(\widehat{B})+Var(\widehat{C}) \\ & & +{{\widehat{C}}^{2}}{{\left( \ln (U) \right)}^{2}}Var(\widehat{n}) \\ & & +\frac{2\widehat{C}}{V}Cov(\widehat{B},\widehat{C}) \\ & & -\frac{2{{\widehat{C}}^{2}}\ln (U)}{V}Cov(\widehat{B},\widehat{n}) \\ & & -2\widehat{C}\ln (U)Cov(\widehat{C},\widehat{n})] \end{align} }[/math]

The variances and covariance of [math]\displaystyle{ B, }[/math] [math]\displaystyle{ C }[/math] and [math]\displaystyle{ n }[/math] are estimated from the local Fisher matrix (evaluated at [math]\displaystyle{ \widehat{B}, }[/math] [math]\displaystyle{ \widehat{C}, }[/math] [math]\displaystyle{ \widehat{n}) }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var(\widehat{B}) & Cov(\widehat{B},\widehat{C}) & Cov(\widehat{B},\widehat{n}) \\ Cov(\widehat{C},\widehat{B}) & Var(\widehat{C}) & Cov(\widehat{C},\widehat{n}) \\ Cov(\widehat{n},\widehat{B}) & Cov(\widehat{n},\widehat{C}) & Var(\widehat{n}) \\ \end{matrix} \right]={{\left[ F \right]}^{-1}} }[/math]

where,

[math]\displaystyle{ F=\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{B}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial B\partial C} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial B\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial C\partial B} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{C}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial C\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial B} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial C} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right]. }[/math]

Confidence Bounds on Reliability

The bounds on reliability at a given time, [math]\displaystyle{ T }[/math] , are estimated by:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & {{e}^{-\tfrac{T}{{{m}_{U}}}}} \\ & {{R}_{L}}= & {{e}^{-\tfrac{T}{{{m}_{L}}}}} \end{align} }[/math]

where [math]\displaystyle{ {{m}_{U}} }[/math] and [math]\displaystyle{ {{m}_{L}} }[/math] are estimated using Eqns. (TVuUpper) and (TVuLower).

Confidence Bounds on Time

The bounds on time for a given reliability (ML estimate of time) are estimated by first solving the reliability function with respect to time:

[math]\displaystyle{ \widehat{T}=-\widehat{m}\cdot \ln (R) }[/math]

The corresponding confidence bounds are estimated from:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & -{{m}_{U}}\cdot \ln (R) \\ & {{T}_{L}}= & -{{m}_{L}}\cdot \ln (R) \end{align} }[/math]

where [math]\displaystyle{ {{m}_{U}} }[/math] and [math]\displaystyle{ {{m}_{L}} }[/math] are estimated using Eqns. (TVuUpper) and (TVuLower).

Approximate Confidence Bounds for the T-NT Weibull

Bounds on the Parameters

Using the same approach as previously discussed ( [math]\displaystyle{ \widehat{\beta } }[/math] and
[math]\displaystyle{ \widehat{C} }[/math] positive parameters):

[math]\displaystyle{ \begin{align} & {{\beta }_{U}}= & \widehat{\beta }\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}} \\ & {{\beta }_{L}}= & \widehat{\beta }\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}} \end{align} }[/math]

[math]\displaystyle{ \begin{align} & {{B}_{U}}= & \widehat{B}+{{K}_{\alpha }}\sqrt{Var(\widehat{B})} \\ & {{B}_{L}}= & \widehat{B}-{{K}_{\alpha }}\sqrt{Var(\widehat{A})} \end{align} }[/math]

[math]\displaystyle{ \begin{align} & {{C}_{U}}= & \widehat{C}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{C})}}{\widehat{C}}}} \\ & {{C}_{L}}= & \widehat{C}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{C})}}{\widehat{C}}}} \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} & {{n}_{U}}= & \widehat{n}+{{K}_{\alpha }}\sqrt{Var(\widehat{n})} \\ & {{n}_{L}}= & \widehat{n}-{{K}_{\alpha }}\sqrt{Var(\widehat{n})} \end{align} }[/math]

The variances and covariances of [math]\displaystyle{ \beta , }[/math] [math]\displaystyle{ B, }[/math] [math]\displaystyle{ C, }[/math] and [math]\displaystyle{ n }[/math] are estimated from the Fisher matrix (evaluated at [math]\displaystyle{ \widehat{\beta }, }[/math] [math]\displaystyle{ \widehat{B}, }[/math] [math]\displaystyle{ \widehat{C}, }[/math] [math]\displaystyle{ \widehat{n}) }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var(\widehat{\beta }) & Cov(\widehat{\beta },\widehat{B}) & Cov(\widehat{\beta },\widehat{C}) & Cov(\widehat{\beta },\widehat{n}) \\ Cov(\widehat{B},\widehat{\beta }) & Var(\widehat{B}) & Cov(\widehat{B},\widehat{C}) & Cov(\widehat{B},\widehat{n}) \\ Cov(\widehat{C},\widehat{\beta }) & Cov(\widehat{C},\widehat{B}) & Var(\widehat{C}) & Cov(\widehat{C},\widehat{n}) \\ Cov(\widehat{n},\widehat{\beta }) & Cov(\widehat{n},\widehat{B}) & Cov(\widehat{n},\widehat{C}) & Var(\widehat{n}) \\ \end{matrix} \right]={{\left[ F \right]}^{-1}} }[/math]

where:

[math]\displaystyle{ F=\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\beta }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial B} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial C} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial B\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{B}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial B\partial C} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial B\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial C\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial C\partial B} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{C}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial C\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial B} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial C} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right] }[/math]

Confidence Bounds on Reliability

The reliability function (ML estimate) for the T-NT Weibull model is given by:

[math]\displaystyle{ \widehat{R}(T,U,V)={{e}^{-{{\left( \tfrac{{{U}^{\widehat{n}}}{{e}^{-\tfrac{\widehat{B}}{V}}}}{\widehat{C}}T \right)}^{\widehat{\beta }}}}} }[/math]

or:

[math]\displaystyle{ \widehat{R}(T,U,V)={{e}^{-{{e}^{\ln \left[ {{\left( \tfrac{{{U}^{\widehat{n}}}{{e}^{-\tfrac{\widehat{B}}{V}}}}{\widehat{C}}T \right)}^{\widehat{\beta }}} \right]}}}} }[/math]

Setting:

[math]\displaystyle{ \widehat{u}=\ln \left[ {{\left( \frac{{{U}^{\widehat{n}}}{{e}^{-\tfrac{\widehat{B}}{V}}}}{\widehat{C}}T \right)}^{\widehat{\beta }}} \right] }[/math]

or:

[math]\displaystyle{ \widehat{u}=\widehat{\beta }\left[ \ln (T)-\frac{\widehat{B}}{V}-\ln (\widehat{C})+\widehat{n}\ln (U) \right] }[/math]

The reliability function now becomes:

[math]\displaystyle{ \widehat{R}(T,U,V)={{e}^{-e\widehat{^{u}}}} }[/math]

The next step is to find the upper and lower bounds on [math]\displaystyle{ u }[/math] :

[math]\displaystyle{ {{u}_{U}}=\widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

[math]\displaystyle{ {{u}_{L}}=\widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

where:

[math]\displaystyle{ \begin{align} & Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial B} \right)}^{2}}Var(\widehat{B}) \\ & & +{{\left( \frac{\partial \widehat{u}}{\partial C} \right)}^{2}}Var(\widehat{C})+{{\left( \frac{\partial \widehat{u}}{\partial n} \right)}^{2}}Var(\widehat{n}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial C} \right)Cov(\widehat{\beta },\widehat{B}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial C} \right)Cov(\widehat{\beta },\widehat{C}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{\beta },\widehat{n}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial B} \right)\left( \frac{\partial \widehat{u}}{\partial C} \right)Cov(\widehat{B},\widehat{C}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial B} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{B},\widehat{n}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial C} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{C},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{u})= & {{\left( \frac{\widehat{u}}{\widehat{\beta }} \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\widehat{\beta }}{V} \right)}^{2}}Var(\widehat{B}) \\ & & +{{\left( \frac{\widehat{\beta }}{\widehat{C}} \right)}^{2}}Var(\widehat{C})+{{\left( \widehat{\beta }\ln (U) \right)}^{2}}Var(\widehat{n}) \\ & & -\frac{2\widehat{u}}{V}Cov(\widehat{\beta },\widehat{B})-\frac{2\widehat{u}}{\widehat{C}}Cov(\widehat{\beta },\widehat{C}) \\ & & +2\widehat{u}\ln (U)Cov(\widehat{\beta },\widehat{n}) \\ & & +\frac{2{{\widehat{\beta }}^{2}}}{\widehat{C}V}Cov(\widehat{B},\widehat{C})-\frac{2{{\widehat{\beta }}^{2}}\ln (U)}{V}Cov(\widehat{B},\widehat{n}) \\ & & -\frac{2{{\widehat{\beta }}^{2}}\ln (U)}{\widehat{C}}Cov(\widehat{C},\widehat{n}) \end{align} }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & {{e}^{-{{e}^{\left( {{u}_{L}} \right)}}}} \\ & {{R}_{L}}= & {{e}^{-{{e}^{\left( {{u}_{U}} \right)}}}} \end{align} }[/math]

where [math]\displaystyle{ {{u}_{U}} }[/math] and .. are estimated using Eqns. (TVUupper) and (TVUlower).

Confidence Bounds on Time

The bounds on time (ML estimate of time) for a given reliability are estimated by first solving the reliability function with respect to time as follows:

[math]\displaystyle{ \begin{align} & \ln (R)= & -{{\left( \frac{{{U}^{\widehat{n}}}{{e}^{-\tfrac{\widehat{B}}{V}}}}{\widehat{C}}\widehat{T} \right)}^{\widehat{\beta }}} \\ & \ln (-\ln (R))= & \widehat{\beta }\left( \ln (\widehat{T})-\frac{\widehat{B}}{V}-\ln (\widehat{C})+\widehat{n}\ln (U) \right) \end{align} }[/math]

or:

[math]\displaystyle{ \widehat{u}=\frac{1}{\widehat{\beta }}\ln (-\ln (R))+\frac{\widehat{B}}{V}+\ln (\widehat{C})-\widehat{n}\ln (U) }[/math]

where [math]\displaystyle{ \widehat{u}=\ln \widehat{T}. }[/math]
The upper and lower bounds on [math]\displaystyle{ u }[/math] are estimated from:

[math]\displaystyle{ {{u}_{U}}=\widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

[math]\displaystyle{ {{u}_{L}}=\widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

where:

[math]\displaystyle{ \begin{align} & Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial B} \right)}^{2}}Var(\widehat{B}) \\ & & +{{\left( \frac{\partial \widehat{u}}{\partial C} \right)}^{2}}Var(\widehat{C})+{{\left( \frac{\partial \widehat{u}}{\partial n} \right)}^{2}}Var(\widehat{n}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial C} \right)Cov(\widehat{\beta },\widehat{B}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial C} \right)Cov(\widehat{\beta },\widehat{C}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{\beta },\widehat{n}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial B} \right)\left( \frac{\partial \widehat{u}}{\partial C} \right)Cov(\widehat{B},\widehat{C}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial B} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{B},\widehat{n}) \\ & & +2\left( \frac{\partial \widehat{u}}{\partial C} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{C},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{u})= & \frac{1}{{{\widehat{\beta }}^{4}}}{{\left[ \ln (-\ln (R)) \right]}^{2}}Var(\widehat{\beta }) \\ & & +\frac{1}{{{V}^{2}}}Var(\widehat{B})+\frac{1}{{{\widehat{C}}^{2}}}Var(\widehat{C})+{{\left[ \ln (U) \right]}^{2}}Var(\widehat{n}) \\ & & -\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}V}Cov(\widehat{\beta },\widehat{B}) \\ & & -\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}\widehat{C}}Cov(\widehat{\beta },\widehat{C}) \\ & & +\frac{2\ln (-\ln (R))\ln (U)}{{{\widehat{\beta }}^{2}}}Cov(\widehat{\beta },\widehat{n}) \\ & & +\frac{2}{\widehat{C}V}Cov(\widehat{B},\widehat{C}) \\ & & -\frac{2\ln (U)}{V}Cov(\widehat{B},\widehat{n})-\frac{2\ln (U)}{\widehat{C}}Cov(\widehat{C},\widehat{n}) \end{align} }[/math]

The upper and lower bounds on time are then found by:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & {{e}^{{{u}_{U}}}} \\ & {{T}_{L}}= & {{e}^{{{u}_{L}}}} \end{align} }[/math]

where [math]\displaystyle{ {{u}_{U}} }[/math] and [math]\displaystyle{ {{u}_{L}} }[/math] are estimated using Eqns. (TVUupper) and (TVUlower).

Approximate Confidence Bounds for the T-NT Lognormal

Bounds on the Parameters

Since the standard deviation, [math]\displaystyle{ {{\widehat{\sigma }}_{{{T}'}}} }[/math] , and [math]\displaystyle{ \widehat{C} }[/math] are positive parameters, [math]\displaystyle{ \ln ({{\widehat{\sigma }}_{{{T}'}}}) }[/math] and [math]\displaystyle{ \ln (\widehat{C}) }[/math] are treated as normally distributed and the bounds are estimated from:

[math]\displaystyle{ \begin{align} & {{\sigma }_{U}}= & {{\widehat{\sigma }}_{{{T}'}}}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}}\text{ (Upper bound)} \\ & & \\ & {{\sigma }_{L}}= & \frac{{{\widehat{\sigma }}_{{{T}'}}}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}}}\text{ (Lower bound)} \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} & {{C}_{U}}= & \widehat{C}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{C})}}{\widehat{C}}}}\text{ (Upper bound)} \\ & & \\ & {{C}_{L}}= & \frac{\widehat{A}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{C})}}{\widehat{C}}}}}\text{ (Lower bound)} \end{align} }[/math]

The lower and upper bounds on [math]\displaystyle{ B }[/math] and [math]\displaystyle{ n }[/math] are estimated from:

[math]\displaystyle{ \begin{align} & {{B}_{U}}= & \widehat{B}+{{K}_{\alpha }}\sqrt{Var(\widehat{B})}\text{ (Upper bound)} \\ & & \\ & {{B}_{L}}= & \widehat{B}-{{K}_{\alpha }}\sqrt{Var(\widehat{B})}\text{ (Lower bound)} \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} & {{n}_{U}}= & \widehat{n}+{{K}_{\alpha }}\sqrt{Var(\widehat{n})}\text{ (Upper bound)} \\ & & \\ & {{n}_{L}}= & \widehat{n}-{{K}_{\alpha }}\sqrt{Var(\widehat{n})}\text{ (Lower bound)} \end{align} }[/math]

The variances and covariances of [math]\displaystyle{ B }[/math] , [math]\displaystyle{ C, }[/math] [math]\displaystyle{ n, }[/math] and [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] are estimated from the local Fisher matrix (evaluated at [math]\displaystyle{ \widehat{B}, }[/math] [math]\displaystyle{ \widehat{C}, }[/math] [math]\displaystyle{ \widehat{n} }[/math] , [math]\displaystyle{ {{\widehat{\sigma }}_{{{T}'}}}) }[/math] as follows:

[math]\displaystyle{ \left( \begin{matrix} Var\left( {{\widehat{\sigma }}_{{{T}'}}} \right) & Cov\left( \widehat{B},{{\widehat{\sigma }}_{{{T}'}}} \right) & Cov\left( \widehat{C},{{\widehat{\sigma }}_{{{T}'}}} \right) & Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) \\ Cov\left( {{\widehat{\sigma }}_{{{T}'}}},\widehat{B} \right) & Var\left( \widehat{B} \right) & Cov\left( \widehat{B},\widehat{C} \right) & Cov\left( \widehat{B},\widehat{n} \right) \\ Cov\left( {{\widehat{\sigma }}_{{{T}'}}},\widehat{C} \right) & Cov\left( \widehat{C},\widehat{B} \right) & Var\left( \widehat{C} \right) & Cov\left( \widehat{C},\widehat{n} \right) \\ Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) & Cov\left( \widehat{n},\widehat{B} \right) & Cov\left( \widehat{n},\widehat{C} \right) & Var\left( \widehat{n} \right) \\ \end{matrix} \right)={{\left[ F \right]}^{-1}} }[/math]

where:

[math]\displaystyle{ F=\left( \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial \sigma _{{{T}'}}^{2}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial B} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial C} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial B\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{B}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial B\partial C} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial B\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial C\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial C\partial B} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{C}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial C\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial B} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial C} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right) }[/math]

Bounds on Reliability

The reliability of the lognormal distribution is given by:

[math]\displaystyle{ R({T}',U,V;B,C,n,{{\sigma }_{{{T}'}}})=\mathop{}_{{{T}'}}^{\infty }\frac{1}{{{\widehat{\sigma }}_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t-\ln (\widehat{C})+\widehat{n}\ln ({{U}_{i}})-\tfrac{\widehat{B}}{{{V}_{i}}}}{{{\widehat{\sigma }}_{{{T}'}}}} \right)}^{2}}}}dt }[/math]

Let [math]\displaystyle{ \widehat{z}(t,U,V;B,C,n,{{\sigma }_{T}})=\tfrac{t-\ln (\widehat{C})+\widehat{n}\ln (U)-\tfrac{\widehat{B}}{V}}{{{\widehat{\sigma }}_{{{T}'}}}}, }[/math] then [math]\displaystyle{ \tfrac{d\widehat{z}}{dt}=\tfrac{1}{{{\widehat{\sigma }}_{{{T}'}}}}. }[/math] For [math]\displaystyle{ t={T}' }[/math] , [math]\displaystyle{ \widehat{z}=\tfrac{{T}'-\ln (\widehat{C})+\widehat{n}\ln (U)-\tfrac{\widehat{B}}{V}}{{{\widehat{\sigma }}_{{{T}'}}}} }[/math] , and for [math]\displaystyle{ t=\infty , }[/math] [math]\displaystyle{ \widehat{z}=\infty . }[/math]

The above equation then becomes:

[math]\displaystyle{ R(\widehat{z})=\mathop{}_{\widehat{z}({T}',U,V)}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz }[/math]

The bounds on [math]\displaystyle{ z }[/math] are estimated from:

[math]\displaystyle{ \begin{align} & {{z}_{U}}= & \widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \\ & {{z}_{L}}= & \widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & Var(\widehat{z})= & \left( \frac{\partial \widehat{z}}{\partial B} \right)_{\widehat{B}}^{2}Var(\widehat{B})+\left( \frac{\partial \widehat{z}}{\partial C} \right)_{\widehat{C}}^{2}Var(\widehat{C}) \\ & & +\left( \frac{\partial \widehat{z}}{\partial n} \right)_{\widehat{b}}^{2}Var(\widehat{n})+\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)_{{{\widehat{\sigma }}_{{{T}'}}}}^{2}Var({{\widehat{\sigma }}_{{{T}'}}}) \\ & & +2{{\left( \frac{\partial \widehat{z}}{\partial B} \right)}_{\widehat{B}}}{{\left( \frac{\partial \widehat{z}}{\partial C} \right)}_{\widehat{C}}}Cov\left( \widehat{B},\widehat{C} \right) \\ & & +2{{\left( \frac{\partial \widehat{z}}{\partial B} \right)}_{\widehat{B}}}{{\left( \frac{\partial \widehat{z}}{\partial b} \right)}_{\widehat{n}}}Cov\left( \widehat{B},\widehat{n} \right) \\ & & +2{{\left( \frac{\partial \widehat{z}}{\partial C} \right)}_{\widehat{C}}}{{\left( \frac{\partial \widehat{z}}{\partial n} \right)}_{\widehat{n}}}Cov\left( \widehat{C},\widehat{n} \right) \\ & & +2{{\left( \frac{\partial \widehat{z}}{\partial B} \right)}_{\widehat{B}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{B},{{\widehat{\sigma }}_{{{T}'}}} \right) \\ & & +2{{\left( \frac{\partial \widehat{z}}{\partial C} \right)}_{\widehat{C}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{C},{{\widehat{\sigma }}_{{{T}'}}} \right) \\ & & +2{{\left( \frac{\partial \widehat{z}}{\partial n} \right)}_{\widehat{n}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{z})= & \frac{1}{\widehat{\sigma }_{{{T}'}}^{2}}[\frac{1}{{{V}^{2}}}Var(\widehat{B})+\frac{1}{{{C}^{2}}}Var(\widehat{C})+\ln {{(U)}^{2}}Var(\widehat{n})+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) \\ & & +\frac{2}{C\cdot V}Cov\left( \widehat{B},\widehat{C} \right)-\frac{2\ln (U)}{V}Cov\left( \widehat{B},\widehat{n} \right) \\ & & -\frac{2\ln (U)}{C}Cov\left( \widehat{C},\widehat{n} \right)+\frac{2\widehat{z}}{V}Cov\left( \widehat{B},{{\widehat{\sigma }}_{{{T}'}}} \right) \\ & & +\frac{2\widehat{z}}{C}Cov\left( \widehat{C},{{\widehat{\sigma }}_{{{T}'}}} \right)-2\widehat{z}\ln (U)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right)] \end{align} }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & \mathop{}_{{{z}_{L}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Upper bound)} \\ & {{R}_{L}}= & \mathop{}_{{{z}_{U}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Lower bound)} \end{align} }[/math]

Confidence Bounds on Time

The bounds around time for a given lognormal percentile (unreliability) are estimated by first solving the reliability equation with respect to time, as follows:

[math]\displaystyle{ {T}'(U,V;\widehat{B},\widehat{C},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}})=\ln (\widehat{C})+\widehat{n}\ln (U)-\frac{\widehat{B}}{V}+z\cdot {{\widehat{\sigma }}_{{{T}'}}} }[/math]

where:

[math]\displaystyle{ \begin{align} & {T}'(U,V;\widehat{A},\widehat{\phi },\widehat{b},{{\widehat{\sigma }}_{{{T}'}}})= & \ln (T) \\ & z= & {{\Phi }^{-1}}\left[ F({T}') \right] \end{align} }[/math]

and:

[math]\displaystyle{ \Phi (z)=\frac{1}{\sqrt{2\pi }}\mathop{}_{-\infty }^{z({T}',U,V)}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz }[/math]

The next step is to calculate the variance of [math]\displaystyle{ {T}'(U,V;\widehat{B},\widehat{C},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}}) }[/math] :

[math]\displaystyle{ \begin{align} & Var({T}')= & {{\left( \frac{\partial {T}'}{\partial B} \right)}^{2}}Var(\widehat{B})+{{\left( \frac{\partial {T}'}{\partial C} \right)}^{2}}Var(\widehat{C}) \\ & & +{{\left( \frac{\partial {T}'}{\partial n} \right)}^{2}}Var(\widehat{n})+{{\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) \\ & & +2\left( \frac{\partial {T}'}{\partial B} \right)\left( \frac{\partial {T}'}{\partial C} \right)Cov\left( \widehat{B},\widehat{C} \right) \\ & & +2\left( \frac{\partial {T}'}{\partial B} \right)\left( \frac{\partial {T}'}{\partial n} \right)Cov\left( \widehat{B},\widehat{n} \right) \\ & & +2\left( \frac{\partial {T}'}{\partial C} \right)\left( \frac{\partial {T}'}{\partial n} \right)Cov\left( \widehat{C},\widehat{n} \right) \\ & & +2\left( \frac{\partial {T}'}{\partial B} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{B},{{\widehat{\sigma }}_{{{T}'}}} \right) \\ & & +2\left( \frac{\partial {T}'}{\partial C} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{C},{{\widehat{\sigma }}_{{{T}'}}} \right) \\ & & +2\left( \frac{\partial {T}'}{\partial n} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) \end{align} }[/math]

or:

The upper and lower bounds are then found by:

[math]\displaystyle{ \begin{align} & T_{U}^{\prime }= & \ln {{T}_{U}}={T}'+{{K}_{\alpha }}\sqrt{Var({T}')} \\ & T_{L}^{\prime }= & \ln {{T}_{L}}={T}'-{{K}_{\alpha }}\sqrt{Var({T}')} \end{align} }[/math]

Solving for [math]\displaystyle{ {{T}_{U}} }[/math] and [math]\displaystyle{ {{T}_{L}} }[/math] yields:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & {{e}^{T_{U}^{\prime }}}\text{ (Upper bound)} \\ & {{T}_{L}}= & {{e}^{T_{L}^{\prime }}}\text{ (Lower bound)} \end{align} }[/math]