Complex Failure Modes Example

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.

---

This example appears in the Life Data Analysis Reference book.

Assume that a product has five independent failure modes: A, B, C, D and E. Furthermore, assume that failure of the product will occur if mode A occurs, modes B and C occur simultaneously or if modes D and E occur simultaneously. The objective is to estimate the reliability of the product at 100 hours, with 90% two-sided confidence bounds. The times-to-failure data for each mode are given in the following table.

[math]\displaystyle{ \begin{matrix} \text{TTF for A} & \text{TTF for B} & \text{TTF for C} & \text{TTF for D} & \text{TTF for E} \\ \text{276} & \text{23} & \text{499} & \text{467} & \text{67} \\ \text{320} & \text{36} & \text{545} & \text{540} & \text{72} \\ \text{323} & \text{57} & \text{661} & \text{716} & \text{81} \\ \text{558} & \text{89} & \text{738} & \text{737} & \text{108} \\ \text{674} & \text{99} & \text{987} & \text{761} & \text{110} \\ \text{829} & \text{154} & \text{1165} & \text{1093} & \text{127} \\ \text{878} & \text{200} & \text{1337} & \text{1283} & \text{148} \\ \end{matrix} }[/math]

Solution

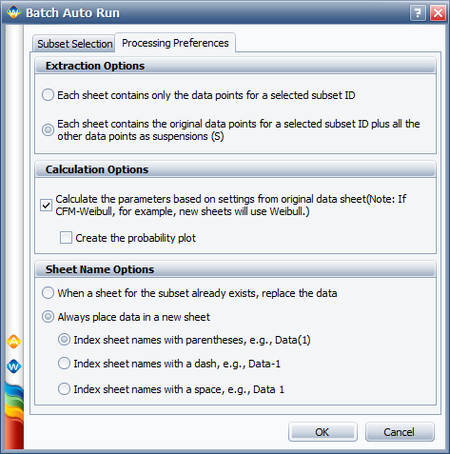
The reliability block diagram (RBD) approach can be used to analyze the failure modes. But before creating a diagram, the data sets of the failure modes need to be segregated so that each mode can be represented by a single block in the diagram. Recall that when you analyze a particular mode, the failure times for all other unrelated modes are considered to be suspensions. This captures the fact that those units operated for a period of time without experiencing the failure mode of interest before they were removed from observation when they failed due to another mode. We can easily perform this step via Weibull++'s Batch Auto Run utility. To do this, enter the data from the table into a single data sheet. Choose the 2P-Weibull distribution and the MLE analysis method, and then click the Batch Auto Run icon on the control panel. When prompted to select the subset IDs, select them all. Click the Processing Preferences tab. In the Extraction Options area, select the second option, as shown next.

This will extract the data sets that are required for the analysis. Select the check box in the Calculation Options area and click OK. The data sets are extracted into separate data sheets in the folio and automatically calculated.

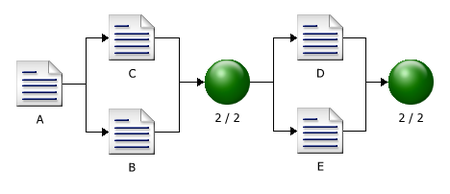
Next, create a diagram by choosing Insert > Tools > Diagram. Add blocks by right-clicking the diagram and choosing Add Block on the shortcut menu. When prompted to select the data sheet of the failure mode that the block will represent, select the data sheet for mode A. Use the same approach to add the blocks that will represent failure modes B, C , D and E. Add a connector by right-clicking the diagram sheet and choosing Connect Blocks, and then connect the blocks in an appropriate configuration to describe the relationships between the failure modes. To insert a node, which acts as a switch that the diagram paths move through, right-click the diagram and choose Add Node. Specify the number of required paths in the node by double-clicking the node and entering the appropriate number (use 2 in both nodes).

The following figure shows the completed diagram.

Click Analyze to analyze the diagram, and then use the Quick Calculation Pad (QCP) to estimate the reliability. The estimated R( [math]\displaystyle{ 100 }[/math] hours [math]\displaystyle{ ) }[/math] and the 90% two-sided confidence bounds are:

[math]\displaystyle{ \begin{matrix} {{{\hat{R}}}_{U}}(100)=0.895940 \\ \hat{R}(100)=0.824397 \\ {{{\hat{R}}}_{L}}(100)=0.719090 \\ \end{matrix} }[/math]