Eyring Relationship
Introduction
The Eyring relationship was formulated from quantum mechanics principles [9] and is most often used when thermal stress (temperature) is the acceleration variable. However, the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The relationship is given by:
- [math]\displaystyle{ L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (temperature values are in absolute units: kelvin or degrees Rankine).
• [math]\displaystyle{ A }[/math] is one of the model parameters to be determined.
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
The Eyring relationship is similar to the Arrhenius relationship. This similarity is more apparent if it is rewritten in the following way:
- [math]\displaystyle{ \begin{align} L(V)=\ & \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} =\ & \frac{{{e}^{-A}}}{V}{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
or:
- [math]\displaystyle{ L(V)=\frac{1}{V}Const.\cdot {{e}^{\tfrac{B}{V}}} }[/math]
The Arrhenius relationship is given by:
- [math]\displaystyle{ L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
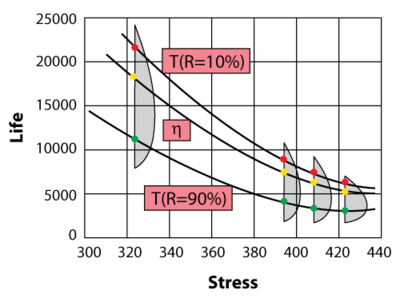
Comparing the above equation to the Arrhenius relationship, it can be seen that the only difference between the two relationships is the [math]\displaystyle{ \tfrac{1}{V} }[/math] term above. In general, both relationships yield very similar results. Like the Arrhenius, the Eyring relationship is plotted on a log-reciprocal paper.
Acceleration Factor
For the Eyring model the acceleration factor is given by:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{{{V}_{u}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{u}}} \right)}}}{\tfrac{1}{{{V}_{A}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{A}}} \right)}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{{{V}_{A}}}{{{V}_{u}}}{{e}^{B\left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)}} }[/math]
Eyring-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda \cdot {{e}^{-\lambda \cdot t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}\cdot {{e}^{-\tfrac{t}{m}}} }[/math]
The Eyring-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
- [math]\displaystyle{ m=L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
and substituting for [math]\displaystyle{ m }[/math] in the exponential [math]\displaystyle{ pdf }[/math] equation:
- [math]\displaystyle{ f(t,V)=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}\cdot t}} }[/math]
Eyring-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) for the Eyring-exponential is given by:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-tV{{e}^{\left( A-\tfrac{B}{V} \right)}}}}dt =\ \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T}, }[/math] for the Eyring-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-exponential model is [math]\displaystyle{ \tilde{T}=0. }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math], for the Eyring-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Eyring-Exponential Reliability Function
The Eyring-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
This function is the complement of the Eyring-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}dT={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Conditional Reliability
The conditional reliability function for the Eyring-exponential model is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Reliable Life
For the Eyring-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete exponential log-likelihood function of the Eyring model is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{e}^{-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot {{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
- where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the first of two parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the second of two parameters to be estimated).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{A} }[/math] and [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( 1-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left[ {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}}-\frac{1}{{{V}_{i}}} \right]+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
Eyring-Weibull
The [math]\displaystyle{ pdf }[/math] for 2-parameter Weibull distribution is given by:
- [math]\displaystyle{ f(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{\eta } \right)}^{\beta }}}} }[/math]
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] . The Eyring-Weibull model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ \frac{1}{\eta }=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
Substituting for [math]\displaystyle{ \eta }[/math] into the Weibull [math]\displaystyle{ pdf }[/math] yields:
- [math]\displaystyle{ f(t,V)=\beta \cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}}{{e}^{-{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Eyring-Weibull Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T} }[/math], or Mean Time To Failure (MTTF) for the Eyring-Weibull model is given by:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right) }[/math]
where [math]\displaystyle{ \Gamma \left( \tfrac{1}{\beta }+1 \right) }[/math] is the gamma function evaluated at the value of [math]\displaystyle{ \left( \tfrac{1}{\beta }+1 \right) }[/math] .
Median
The median, [math]\displaystyle{ \breve{T} }[/math] for the Eyring-Weibull model is given by:
- [math]\displaystyle{ \breve{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}{{\left( \ln 2 \right)}^{\tfrac{1}{\beta }}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-Weibull model is given by:
- [math]\displaystyle{ \tilde{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}{{\left( 1-\frac{1}{\beta } \right)}^{\tfrac{1}{\beta }}} }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}}, }[/math] for the Eyring-Weibull model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \sqrt{\Gamma \left( \frac{2}{\beta }+1 \right)-{{\left( \Gamma \left( \frac{1}{\beta }+1 \right) \right)}^{2}}} }[/math]
Eyring-Weibull Reliability Function
The Eyring-Weibull reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-{{\left( V\cdot T\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Conditional Reliability Function
The Eyring-Weibull conditional reliability function at a specified stress level is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-{{\left( \left( T+t \right)\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}}}{{{e}^{-{{\left( V\cdot T\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}}} }[/math]
or:
- [math]\displaystyle{ R(T,t,V)={{e}^{-\left[ {{\left( \left( T+t \right)\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}-{{\left( V\cdot T\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }} \right]}} }[/math]
Reliable Life
For the Eyring-Weibull model, the reliable life, [math]\displaystyle{ {{t}_{R}} }[/math] , of a unit for a specified reliability and starting the mission at age zero is given by:
- [math]\displaystyle{ {{t}_{R}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}{{\left\{ -\ln \left[ R\left( {{T}_{R}},V \right) \right] \right\}}^{\tfrac{1}{\beta }}} }[/math]
Eyring-Weibull Failure Rate Function
The Eyring-Weibull failure rate function, [math]\displaystyle{ \lambda (T) }[/math] , is given by:
- [math]\displaystyle{ \lambda \left( T,V \right)=\frac{f\left( T,V \right)}{R\left( T,V \right)}=\beta {{\left( T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}} }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The Eyring-Weibull log-likelihood function is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \beta \cdot {{V}_{i}}\cdot {{e}^{A-\tfrac{B}{{{V}_{i}}}}}{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta -1}}{{e}^{-{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( {{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}T_{i}^{\prime } \right)}^{\beta }}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-{{\left( T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-{{\left( T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure data points in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ \beta }[/math] is the Weibull shape parameter (unknown, the first of three parameters to be estimated).
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the second of three parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the third of three parameters to be estimated).
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the i [math]\displaystyle{ ^{th} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the i [math]\displaystyle{ ^{th} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the i [math]\displaystyle{ ^{th} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \beta , }[/math] [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \beta }=0, }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math]
where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}-\beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} -\beta \underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( T_{i}^{\prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} \overset{FI}{\mathop{-\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\beta V_{i}^{\beta }{{e}^{A\beta -\tfrac{B\beta }{{{V}_{i}}}}}\left[ {{(T_{Li}^{\prime \prime })}^{\beta }}R_{Li}^{\prime \prime }-{{(T_{Ri}^{\prime \prime })}^{\beta }}R_{Ri}^{\prime \prime } \right]}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & -\beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}\frac{1}{{{V}_{i}}}+\beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}\frac{1}{{{V}_{i}}}{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} +\beta \underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }\frac{1}{{{V}_{i}}}{{\left( T_{i}^{\prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} +\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\beta V_{i}^{(\beta -1)}{{e}^{A\beta -\tfrac{B\beta }{{{V}_{i}}}}}\left[ {{(T_{Li}^{\prime \prime })}^{\beta }}R_{Li}^{\prime \prime }-{{(T_{Ri}^{\prime \prime })}^{\beta }}R_{Ri}^{\prime \prime } \right]}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda}{\partial \beta}= & \frac{1}{\beta}\sum_{i=1}^{F_e} N_i\frac{1}{V_i}+\sum_{i=1}^{F_e} N_i ln\left(T_iV_i e^{A-\tfrac{B}{V_i}}\right) -\sum_{i=1}^{F_e} N_i\left(T_iV_i e^{A-\tfrac{B}{V_i}}\right)^\beta ln\left(T_iV)i e^{A-\tfrac{B}{V_i}}\right)\\ & -\sum_{i=1}^S N_i^'\left(T_i^'V_I e^{A-\tfrac{B}{V_i}}\right)^\beta ln\left(T_iV)i e^{A-\tfrac{B}{V_i}}\right) -\sum_{i=1}^{FI} N_i^{''}V_i e^{A-\tfrac{B}{V_i}}\frac{R_{Li}^{''} T_{Li}^{''}\left(ln(T_{Li}^' V_i)+A-\tfrac{B}{V_i}\right)-R_{Ri}^{''} T_{Ri}^{''}\left(ln(T_{Ri}^{''} V_i)+A-\tfrac{B}{V_i}\right)}{R_{L_i}^{''}-F_{Ri}^{''}} \end{align} }[/math]
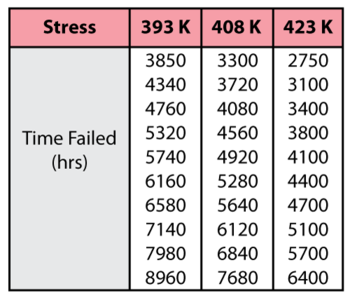
Consider the following times-to-failure data at three different stress levels.
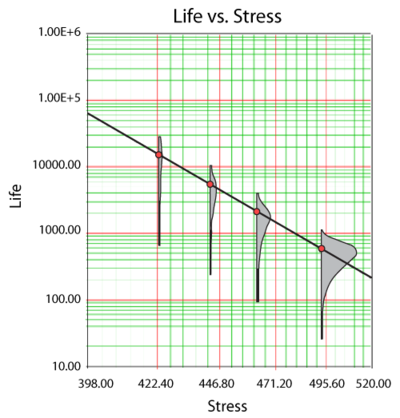
The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding:
- [math]\displaystyle{ \widehat{\beta }=4.29186497\,\! }[/math]
- [math]\displaystyle{ \widehat{A}=-11.08784624\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1454.08635742\,\! }[/math]
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align}\,\! }[/math]
Eyring-Lognormal
The [math]\displaystyle{ pdf }[/math] of the lognormal distribution is given by:
- [math]\displaystyle{ f(T)=\frac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\overline{{{T}'}}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}} }[/math]
where:
- [math]\displaystyle{ {T}'=\ln (T) }[/math]
- [math]\displaystyle{ T=\text{times-to-failure} }[/math]
and
• [math]\displaystyle{ \overline{{{T}'}}= }[/math] mean of the natural logarithms of the times-to-failure.
• [math]\displaystyle{ {{\sigma }_{{{T}'}}}= }[/math] standard deviation of the natural logarithms of the times-to-failure.
The Eyring-lognormal model can be obtained first by setting [math]\displaystyle{ \breve{T}=L(V) }[/math]:
- [math]\displaystyle{ \breve{T}=L(V)=\frac{1}{V}{{e}^{-(A-\tfrac{B}{V})}} }[/math]
or:
- [math]\displaystyle{ {{e}^{{{\overline{T}}^{\prime }}}}=\frac{1}{V}{{e}^{-(A-\tfrac{B}{V})}} }[/math]
Thus:
- [math]\displaystyle{ {{\overline{T}}^{\prime }}=-\ln (V)-A+\frac{B}{V} }[/math]
Substituting this into the lognormal [math]\displaystyle{ pdf }[/math] yields the Eyring-lognormal model [math]\displaystyle{ pdf }[/math]:
- [math]\displaystyle{ f(T,V)=\frac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}} }[/math]
Eyring-Lognormal Statistical Properties Summary
The Mean
The mean life of the Eyring-lognormal model (mean of the times-to-failure), [math]\displaystyle{ \bar{T} }[/math] , is given by:
- [math]\displaystyle{ \begin{align} \bar{T}=\ {{e}^{\bar{{T}'}+\tfrac{1}{2}\sigma _{{{T}'}}^{2}}} =\ {{e}^{-\ln (V)-A+\tfrac{B}{V}+\tfrac{1}{2}\sigma _{{{T}'}}^{2}}} \end{align} }[/math]
The mean of the natural logarithms of the times-to-failure, [math]\displaystyle{ {{\bar{T}}^{^{\prime }}} }[/math] , in terms of [math]\displaystyle{ \bar{T} }[/math] and [math]\displaystyle{ {{\sigma }_{T}} }[/math] is given by:
- [math]\displaystyle{ {{\bar{T}}^{\prime }}=\ln \left( {\bar{T}} \right)-\frac{1}{2}\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right) }[/math]
The Median
The median of the Eyring-lognormal model is given by:
- [math]\displaystyle{ \breve{T}={{e}^{{{\overline{T}}^{\prime }}}} }[/math]
The Standard Deviation
The standard deviation of the Eyring-lognormal model (standard deviation of the times-to-failure), [math]\displaystyle{ {{\sigma }_{T}} }[/math] , is given by:
- [math]\displaystyle{ \begin{align} & {{\sigma }_{T}}= & \sqrt{\left( {{e}^{2\bar{{T}'}+\sigma _{{{T}'}}^{2}}} \right)\left( {{e}^{\sigma _{{{T}'}}^{2}}}-1 \right)} =\ \sqrt{\left( {{e}^{2\left( -\ln (V)-A+\tfrac{B}{V} \right)+\sigma _{{{T}'}}^{2}}} \right)\left( {{e}^{\sigma _{{{T}'}}^{2}}}-1 \right)} \end{align} }[/math]
The standard deviation of the natural logarithms of the times-to-failure, [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] , in terms of [math]\displaystyle{ \bar{T} }[/math] and [math]\displaystyle{ {{\sigma }_{T}} }[/math] is given by:
- [math]\displaystyle{ {{\sigma }_{{{T}'}}}=\sqrt{\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)} }[/math]
The Mode
The mode of the Eyring-lognormal model is given by:
- [math]\displaystyle{ \begin{align} & \tilde{T}= & {{e}^{{{\overline{T}}^{\prime }}-\sigma _{{{T}'}}^{2}}} =\ {{e}^{-\ln (V)-A+\tfrac{B}{V}-\sigma _{{{T}'}}^{2}}} \end{align} }[/math]
Eyring-Lognormal Reliability Function
The reliability for a mission of time [math]\displaystyle{ T }[/math] , starting at age 0, for the Eyring-lognormal model is determined by:
- [math]\displaystyle{ R(T,V)=\int_{T}^{\infty }f(t,V)dt }[/math]
or:
- [math]\displaystyle{ R(T,V)=\int_{{{T}^{^{\prime }}}}^{\infty }\frac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}dt }[/math]
There is no closed form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability we will not discuss manual solution methods.
Reliable Life
For the Eyring-lognormal model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}, }[/math] is estimated by first solving the reliability equation with respect to time, as follows:
- [math]\displaystyle{ T_{R}^{\prime }=-\ln (V)-A+\frac{B}{V}+z\cdot {{\sigma }_{{{T}'}}} }[/math]
where:
- [math]\displaystyle{ z={{\Phi }^{-1}}\left[ F\left( T_{R}^{\prime },V \right) \right] }[/math]
and:
- [math]\displaystyle{ \Phi (z)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{z({T}',V)}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt }[/math]
Since [math]\displaystyle{ {T}'=\ln (T) }[/math] the reliable life, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ {{t}_{R}}={{e}^{T_{R}^{\prime }}} }[/math]
Eyring-Lognormal Failure Rate
The Eyring-lognormal failure rate is given by:
- [math]\displaystyle{ \lambda (T,V)=\frac{f(T,V)}{R(T,V)}=\frac{\tfrac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}}{\int_{{{T}'}}^{\infty }\tfrac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}dt} }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete Eyring-lognormal log-likelihood function is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{{{\sigma }_{{{T}'}}}{{T}_{i}}}\phi \left( \frac{\ln \left( {{T}_{i}} \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right) \right] \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ 1-\Phi \left( \frac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right) \right] +\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]
where:
- [math]\displaystyle{ z_{Li}^{\prime \prime }=\frac{\ln T_{Li}^{\prime \prime }+\ln {{V}_{i}}+A-\tfrac{B}{{{V}_{i}}}}{\sigma _{T}^{\prime }} }[/math]
- [math]\displaystyle{ z_{Ri}^{\prime \prime }=\frac{\ln T_{Ri}^{\prime \prime }+\ln {{V}_{i}}+A-\tfrac{B}{{{V}_{i}}}}{\sigma _{T}^{\prime }} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure data points in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] is the standard deviation of the natural logarithm of the times-to-failure (unknown, the first of three parameters to be estimated).
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the second of three parameters to be estimated).
• [math]\displaystyle{ C }[/math] is the second Eyring parameter (unknown, the third of three parameters to be estimated).
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the i [math]\displaystyle{ ^{th} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for [math]\displaystyle{ {{\widehat{\sigma }}_{{{T}'}}}, }[/math] [math]\displaystyle{ \widehat{A}, }[/math] [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}=0, }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] :
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & -\frac{1}{\sigma _{{{T}'}}^{2}}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}(\ln ({{T}_{i}})+\ln ({{V}_{i}})+A-\frac{B}{{{V}_{i}}}) -\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)} \overset{FI}{\mathop{+\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\varphi (z_{Ri}^{\prime \prime })-\varphi (z_{Li}^{\prime \prime })}{\sigma _{T}^{\prime }(\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime }))} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= \frac{1}{\sigma _{{{T}'}}^{2}}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\frac{1}{{{V}_{i}}}(\ln ({{T}_{i}})+\ln ({{V}_{i}})+A-\frac{B}{{{V}_{i}}}) +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{1}{{{V}_{i}}}\frac{\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)} \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\varphi (z_{Ri}^{\prime \prime })-\varphi (z_{Li}^{\prime \prime })}{\sigma _{T}^{\prime }{{V}_{i}}(\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime }))} \\ & \frac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}= \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{\left( \ln ({{T}_{i}})+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}} \right)}^{2}}}{\sigma _{{{T}'}}^{3}}-\frac{1}{{{\sigma }_{{{T}'}}}} \right) +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)} \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{z_{Ri}^{\prime \prime }\varphi (z_{Ri}^{\prime \prime })-z_{Li}^{\prime \prime }\varphi (z_{Li}^{\prime \prime })}{\sigma _{T}^{\prime }(\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime }))} \end{align} }[/math]
and:
- [math]\displaystyle{ \phi \left( x \right)=\frac{1}{\sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( x \right)}^{2}}}} }[/math]
- [math]\displaystyle{ \Phi (x)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt }[/math]
Introduction
The Eyring relationship was formulated from quantum mechanics principles [9] and is most often used when thermal stress (temperature) is the acceleration variable. However, the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The relationship is given by:
- [math]\displaystyle{ L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (temperature values are in absolute units: kelvin or degrees Rankine).
• [math]\displaystyle{ A }[/math] is one of the model parameters to be determined.
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
The Eyring relationship is similar to the Arrhenius relationship. This similarity is more apparent if it is rewritten in the following way:
- [math]\displaystyle{ \begin{align} L(V)=\ & \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} =\ & \frac{{{e}^{-A}}}{V}{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
or:
- [math]\displaystyle{ L(V)=\frac{1}{V}Const.\cdot {{e}^{\tfrac{B}{V}}} }[/math]
The Arrhenius relationship is given by:
- [math]\displaystyle{ L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
Comparing the above equation to the Arrhenius relationship, it can be seen that the only difference between the two relationships is the [math]\displaystyle{ \tfrac{1}{V} }[/math] term above. In general, both relationships yield very similar results. Like the Arrhenius, the Eyring relationship is plotted on a log-reciprocal paper.
Acceleration Factor
For the Eyring model the acceleration factor is given by:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{{{V}_{u}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{u}}} \right)}}}{\tfrac{1}{{{V}_{A}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{A}}} \right)}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{{{V}_{A}}}{{{V}_{u}}}{{e}^{B\left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)}} }[/math]
Eyring-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda \cdot {{e}^{-\lambda \cdot t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}\cdot {{e}^{-\tfrac{t}{m}}} }[/math]
The Eyring-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
- [math]\displaystyle{ m=L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
and substituting for [math]\displaystyle{ m }[/math] in the exponential [math]\displaystyle{ pdf }[/math] equation:
- [math]\displaystyle{ f(t,V)=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}\cdot t}} }[/math]
Eyring-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) for the Eyring-exponential is given by:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-tV{{e}^{\left( A-\tfrac{B}{V} \right)}}}}dt =\ \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T}, }[/math] for the Eyring-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-exponential model is [math]\displaystyle{ \tilde{T}=0. }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math], for the Eyring-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Eyring-Exponential Reliability Function
The Eyring-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
This function is the complement of the Eyring-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}dT={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Conditional Reliability
The conditional reliability function for the Eyring-exponential model is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Reliable Life
For the Eyring-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete exponential log-likelihood function of the Eyring model is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{e}^{-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot {{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
- where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the first of two parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the second of two parameters to be estimated).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{A} }[/math] and [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( 1-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left[ {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}}-\frac{1}{{{V}_{i}}} \right]+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
Eyring-Weibull
The [math]\displaystyle{ pdf }[/math] for 2-parameter Weibull distribution is given by:
- [math]\displaystyle{ f(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{\eta } \right)}^{\beta }}}} }[/math]
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] . The Eyring-Weibull model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ \frac{1}{\eta }=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
Substituting for [math]\displaystyle{ \eta }[/math] into the Weibull [math]\displaystyle{ pdf }[/math] yields:
- [math]\displaystyle{ f(t,V)=\beta \cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}}{{e}^{-{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Eyring-Weibull Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T} }[/math], or Mean Time To Failure (MTTF) for the Eyring-Weibull model is given by:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right) }[/math]
where [math]\displaystyle{ \Gamma \left( \tfrac{1}{\beta }+1 \right) }[/math] is the gamma function evaluated at the value of [math]\displaystyle{ \left( \tfrac{1}{\beta }+1 \right) }[/math] .
Median
The median, [math]\displaystyle{ \breve{T} }[/math] for the Eyring-Weibull model is given by:
- [math]\displaystyle{ \breve{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}{{\left( \ln 2 \right)}^{\tfrac{1}{\beta }}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-Weibull model is given by:
- [math]\displaystyle{ \tilde{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}{{\left( 1-\frac{1}{\beta } \right)}^{\tfrac{1}{\beta }}} }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}}, }[/math] for the Eyring-Weibull model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \sqrt{\Gamma \left( \frac{2}{\beta }+1 \right)-{{\left( \Gamma \left( \frac{1}{\beta }+1 \right) \right)}^{2}}} }[/math]
Eyring-Weibull Reliability Function
The Eyring-Weibull reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-{{\left( V\cdot T\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Conditional Reliability Function
The Eyring-Weibull conditional reliability function at a specified stress level is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-{{\left( \left( T+t \right)\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}}}{{{e}^{-{{\left( V\cdot T\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}}} }[/math]
or:
- [math]\displaystyle{ R(T,t,V)={{e}^{-\left[ {{\left( \left( T+t \right)\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}-{{\left( V\cdot T\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }} \right]}} }[/math]
Reliable Life
For the Eyring-Weibull model, the reliable life, [math]\displaystyle{ {{t}_{R}} }[/math] , of a unit for a specified reliability and starting the mission at age zero is given by:
- [math]\displaystyle{ {{t}_{R}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}{{\left\{ -\ln \left[ R\left( {{T}_{R}},V \right) \right] \right\}}^{\tfrac{1}{\beta }}} }[/math]
Eyring-Weibull Failure Rate Function
The Eyring-Weibull failure rate function, [math]\displaystyle{ \lambda (T) }[/math] , is given by:
- [math]\displaystyle{ \lambda \left( T,V \right)=\frac{f\left( T,V \right)}{R\left( T,V \right)}=\beta {{\left( T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}} }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The Eyring-Weibull log-likelihood function is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \beta \cdot {{V}_{i}}\cdot {{e}^{A-\tfrac{B}{{{V}_{i}}}}}{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta -1}}{{e}^{-{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( {{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}T_{i}^{\prime } \right)}^{\beta }}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-{{\left( T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-{{\left( T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure data points in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ \beta }[/math] is the Weibull shape parameter (unknown, the first of three parameters to be estimated).
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the second of three parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the third of three parameters to be estimated).
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the i [math]\displaystyle{ ^{th} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the i [math]\displaystyle{ ^{th} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the i [math]\displaystyle{ ^{th} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \beta , }[/math] [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \beta }=0, }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math]
where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}-\beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} -\beta \underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( T_{i}^{\prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} \overset{FI}{\mathop{-\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\beta V_{i}^{\beta }{{e}^{A\beta -\tfrac{B\beta }{{{V}_{i}}}}}\left[ {{(T_{Li}^{\prime \prime })}^{\beta }}R_{Li}^{\prime \prime }-{{(T_{Ri}^{\prime \prime })}^{\beta }}R_{Ri}^{\prime \prime } \right]}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & -\beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}\frac{1}{{{V}_{i}}}+\beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}\frac{1}{{{V}_{i}}}{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} +\beta \underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }\frac{1}{{{V}_{i}}}{{\left( T_{i}^{\prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} +\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\beta V_{i}^{(\beta -1)}{{e}^{A\beta -\tfrac{B\beta }{{{V}_{i}}}}}\left[ {{(T_{Li}^{\prime \prime })}^{\beta }}R_{Li}^{\prime \prime }-{{(T_{Ri}^{\prime \prime })}^{\beta }}R_{Ri}^{\prime \prime } \right]}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda}{\partial \beta}= & \frac{1}{\beta}\sum_{i=1}^{F_e} N_i\frac{1}{V_i}+\sum_{i=1}^{F_e} N_i ln\left(T_iV_i e^{A-\tfrac{B}{V_i}}\right) -\sum_{i=1}^{F_e} N_i\left(T_iV_i e^{A-\tfrac{B}{V_i}}\right)^\beta ln\left(T_iV)i e^{A-\tfrac{B}{V_i}}\right)\\ & -\sum_{i=1}^S N_i^'\left(T_i^'V_I e^{A-\tfrac{B}{V_i}}\right)^\beta ln\left(T_iV)i e^{A-\tfrac{B}{V_i}}\right) -\sum_{i=1}^{FI} N_i^{''}V_i e^{A-\tfrac{B}{V_i}}\frac{R_{Li}^{''} T_{Li}^{''}\left(ln(T_{Li}^' V_i)+A-\tfrac{B}{V_i}\right)-R_{Ri}^{''} T_{Ri}^{''}\left(ln(T_{Ri}^{''} V_i)+A-\tfrac{B}{V_i}\right)}{R_{L_i}^{''}-F_{Ri}^{''}} \end{align} }[/math]
Consider the following times-to-failure data at three different stress levels.
The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding:
- [math]\displaystyle{ \widehat{\beta }=4.29186497\,\! }[/math]
- [math]\displaystyle{ \widehat{A}=-11.08784624\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1454.08635742\,\! }[/math]
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align}\,\! }[/math]
Eyring-Lognormal
The [math]\displaystyle{ pdf }[/math] of the lognormal distribution is given by:
- [math]\displaystyle{ f(T)=\frac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\overline{{{T}'}}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}} }[/math]
where:
- [math]\displaystyle{ {T}'=\ln (T) }[/math]
- [math]\displaystyle{ T=\text{times-to-failure} }[/math]
and
• [math]\displaystyle{ \overline{{{T}'}}= }[/math] mean of the natural logarithms of the times-to-failure.
• [math]\displaystyle{ {{\sigma }_{{{T}'}}}= }[/math] standard deviation of the natural logarithms of the times-to-failure.
The Eyring-lognormal model can be obtained first by setting [math]\displaystyle{ \breve{T}=L(V) }[/math]:
- [math]\displaystyle{ \breve{T}=L(V)=\frac{1}{V}{{e}^{-(A-\tfrac{B}{V})}} }[/math]
or:
- [math]\displaystyle{ {{e}^{{{\overline{T}}^{\prime }}}}=\frac{1}{V}{{e}^{-(A-\tfrac{B}{V})}} }[/math]
Thus:
- [math]\displaystyle{ {{\overline{T}}^{\prime }}=-\ln (V)-A+\frac{B}{V} }[/math]
Substituting this into the lognormal [math]\displaystyle{ pdf }[/math] yields the Eyring-lognormal model [math]\displaystyle{ pdf }[/math]:
- [math]\displaystyle{ f(T,V)=\frac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}} }[/math]
Eyring-Lognormal Statistical Properties Summary
The Mean
The mean life of the Eyring-lognormal model (mean of the times-to-failure), [math]\displaystyle{ \bar{T} }[/math] , is given by:
- [math]\displaystyle{ \begin{align} \bar{T}=\ {{e}^{\bar{{T}'}+\tfrac{1}{2}\sigma _{{{T}'}}^{2}}} =\ {{e}^{-\ln (V)-A+\tfrac{B}{V}+\tfrac{1}{2}\sigma _{{{T}'}}^{2}}} \end{align} }[/math]
The mean of the natural logarithms of the times-to-failure, [math]\displaystyle{ {{\bar{T}}^{^{\prime }}} }[/math] , in terms of [math]\displaystyle{ \bar{T} }[/math] and [math]\displaystyle{ {{\sigma }_{T}} }[/math] is given by:
- [math]\displaystyle{ {{\bar{T}}^{\prime }}=\ln \left( {\bar{T}} \right)-\frac{1}{2}\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right) }[/math]
The Median
The median of the Eyring-lognormal model is given by:
- [math]\displaystyle{ \breve{T}={{e}^{{{\overline{T}}^{\prime }}}} }[/math]
The Standard Deviation
The standard deviation of the Eyring-lognormal model (standard deviation of the times-to-failure), [math]\displaystyle{ {{\sigma }_{T}} }[/math] , is given by:
- [math]\displaystyle{ \begin{align} & {{\sigma }_{T}}= & \sqrt{\left( {{e}^{2\bar{{T}'}+\sigma _{{{T}'}}^{2}}} \right)\left( {{e}^{\sigma _{{{T}'}}^{2}}}-1 \right)} =\ \sqrt{\left( {{e}^{2\left( -\ln (V)-A+\tfrac{B}{V} \right)+\sigma _{{{T}'}}^{2}}} \right)\left( {{e}^{\sigma _{{{T}'}}^{2}}}-1 \right)} \end{align} }[/math]
The standard deviation of the natural logarithms of the times-to-failure, [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] , in terms of [math]\displaystyle{ \bar{T} }[/math] and [math]\displaystyle{ {{\sigma }_{T}} }[/math] is given by:
- [math]\displaystyle{ {{\sigma }_{{{T}'}}}=\sqrt{\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)} }[/math]
The Mode
The mode of the Eyring-lognormal model is given by:
- [math]\displaystyle{ \begin{align} & \tilde{T}= & {{e}^{{{\overline{T}}^{\prime }}-\sigma _{{{T}'}}^{2}}} =\ {{e}^{-\ln (V)-A+\tfrac{B}{V}-\sigma _{{{T}'}}^{2}}} \end{align} }[/math]
Eyring-Lognormal Reliability Function
The reliability for a mission of time [math]\displaystyle{ T }[/math] , starting at age 0, for the Eyring-lognormal model is determined by:
- [math]\displaystyle{ R(T,V)=\int_{T}^{\infty }f(t,V)dt }[/math]
or:
- [math]\displaystyle{ R(T,V)=\int_{{{T}^{^{\prime }}}}^{\infty }\frac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}dt }[/math]
There is no closed form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability we will not discuss manual solution methods.
Reliable Life
For the Eyring-lognormal model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}, }[/math] is estimated by first solving the reliability equation with respect to time, as follows:
- [math]\displaystyle{ T_{R}^{\prime }=-\ln (V)-A+\frac{B}{V}+z\cdot {{\sigma }_{{{T}'}}} }[/math]
where:
- [math]\displaystyle{ z={{\Phi }^{-1}}\left[ F\left( T_{R}^{\prime },V \right) \right] }[/math]
and:
- [math]\displaystyle{ \Phi (z)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{z({T}',V)}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt }[/math]
Since [math]\displaystyle{ {T}'=\ln (T) }[/math] the reliable life, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ {{t}_{R}}={{e}^{T_{R}^{\prime }}} }[/math]
Eyring-Lognormal Failure Rate
The Eyring-lognormal failure rate is given by:
- [math]\displaystyle{ \lambda (T,V)=\frac{f(T,V)}{R(T,V)}=\frac{\tfrac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}}{\int_{{{T}'}}^{\infty }\tfrac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}dt} }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete Eyring-lognormal log-likelihood function is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{{{\sigma }_{{{T}'}}}{{T}_{i}}}\phi \left( \frac{\ln \left( {{T}_{i}} \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right) \right] \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ 1-\Phi \left( \frac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right) \right] +\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]
where:
- [math]\displaystyle{ z_{Li}^{\prime \prime }=\frac{\ln T_{Li}^{\prime \prime }+\ln {{V}_{i}}+A-\tfrac{B}{{{V}_{i}}}}{\sigma _{T}^{\prime }} }[/math]
- [math]\displaystyle{ z_{Ri}^{\prime \prime }=\frac{\ln T_{Ri}^{\prime \prime }+\ln {{V}_{i}}+A-\tfrac{B}{{{V}_{i}}}}{\sigma _{T}^{\prime }} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure data points in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] is the standard deviation of the natural logarithm of the times-to-failure (unknown, the first of three parameters to be estimated).
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the second of three parameters to be estimated).
• [math]\displaystyle{ C }[/math] is the second Eyring parameter (unknown, the third of three parameters to be estimated).
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the i [math]\displaystyle{ ^{th} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for [math]\displaystyle{ {{\widehat{\sigma }}_{{{T}'}}}, }[/math] [math]\displaystyle{ \widehat{A}, }[/math] [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}=0, }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] :
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & -\frac{1}{\sigma _{{{T}'}}^{2}}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}(\ln ({{T}_{i}})+\ln ({{V}_{i}})+A-\frac{B}{{{V}_{i}}}) -\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)} \overset{FI}{\mathop{+\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\varphi (z_{Ri}^{\prime \prime })-\varphi (z_{Li}^{\prime \prime })}{\sigma _{T}^{\prime }(\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime }))} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= \frac{1}{\sigma _{{{T}'}}^{2}}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\frac{1}{{{V}_{i}}}(\ln ({{T}_{i}})+\ln ({{V}_{i}})+A-\frac{B}{{{V}_{i}}}) +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{1}{{{V}_{i}}}\frac{\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)} \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\varphi (z_{Ri}^{\prime \prime })-\varphi (z_{Li}^{\prime \prime })}{\sigma _{T}^{\prime }{{V}_{i}}(\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime }))} \\ & \frac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}= \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{\left( \ln ({{T}_{i}})+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}} \right)}^{2}}}{\sigma _{{{T}'}}^{3}}-\frac{1}{{{\sigma }_{{{T}'}}}} \right) +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)} \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{z_{Ri}^{\prime \prime }\varphi (z_{Ri}^{\prime \prime })-z_{Li}^{\prime \prime }\varphi (z_{Li}^{\prime \prime })}{\sigma _{T}^{\prime }(\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime }))} \end{align} }[/math]
and:
- [math]\displaystyle{ \phi \left( x \right)=\frac{1}{\sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( x \right)}^{2}}}} }[/math]
- [math]\displaystyle{ \Phi (x)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt }[/math]
Template loop detected: Template:Generalized eyring
Template loop detected: Template:Eyring confidence bounds
Introduction
The Eyring relationship was formulated from quantum mechanics principles [9] and is most often used when thermal stress (temperature) is the acceleration variable. However, the Eyring relationship is also often used for stress variables other than temperature, such as humidity. The relationship is given by:
- [math]\displaystyle{ L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (temperature values are in absolute units: kelvin or degrees Rankine).
• [math]\displaystyle{ A }[/math] is one of the model parameters to be determined.
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
The Eyring relationship is similar to the Arrhenius relationship. This similarity is more apparent if it is rewritten in the following way:
- [math]\displaystyle{ \begin{align} L(V)=\ & \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} =\ & \frac{{{e}^{-A}}}{V}{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
or:
- [math]\displaystyle{ L(V)=\frac{1}{V}Const.\cdot {{e}^{\tfrac{B}{V}}} }[/math]
The Arrhenius relationship is given by:
- [math]\displaystyle{ L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
Comparing the above equation to the Arrhenius relationship, it can be seen that the only difference between the two relationships is the [math]\displaystyle{ \tfrac{1}{V} }[/math] term above. In general, both relationships yield very similar results. Like the Arrhenius, the Eyring relationship is plotted on a log-reciprocal paper.
Acceleration Factor
For the Eyring model the acceleration factor is given by:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{{{V}_{u}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{u}}} \right)}}}{\tfrac{1}{{{V}_{A}}}\text{ }{{e}^{-\left( A-\tfrac{B}{{{V}_{A}}} \right)}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{{{V}_{A}}}{{{V}_{u}}}{{e}^{B\left( \tfrac{1}{{{V}_{u}}}-\tfrac{1}{{{V}_{A}}} \right)}} }[/math]
Eyring-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda \cdot {{e}^{-\lambda \cdot t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}\cdot {{e}^{-\tfrac{t}{m}}} }[/math]
The Eyring-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
- [math]\displaystyle{ m=L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
and substituting for [math]\displaystyle{ m }[/math] in the exponential [math]\displaystyle{ pdf }[/math] equation:
- [math]\displaystyle{ f(t,V)=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}\cdot t}} }[/math]
Eyring-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) for the Eyring-exponential is given by:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-tV{{e}^{\left( A-\tfrac{B}{V} \right)}}}}dt =\ \frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T}, }[/math] for the Eyring-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-exponential model is [math]\displaystyle{ \tilde{T}=0. }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math], for the Eyring-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
Eyring-Exponential Reliability Function
The Eyring-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
This function is the complement of the Eyring-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}V{{e}^{\left( A-\tfrac{B}{V} \right)}}{{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}}dT={{e}^{-T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Conditional Reliability
The conditional reliability function for the Eyring-exponential model is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
Reliable Life
For the Eyring-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-{{t}_{R}}\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete exponential log-likelihood function of the Eyring model is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{e}^{-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot {{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}\cdot T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
- where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the first of two parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the second of two parameters to be estimated).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{A} }[/math] and [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( 1-{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{V}_{i}}\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left[ {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}{{T}_{i}}-\frac{1}{{{V}_{i}}} \right]+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\cdot {{e}^{\left( A-\tfrac{B}{{{V}_{i}}} \right)}}T_{i}^{\prime } \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\left( T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime } \right){{e}^{A-\tfrac{B}{{{V}_{i}}}}}}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
Eyring-Weibull
The [math]\displaystyle{ pdf }[/math] for 2-parameter Weibull distribution is given by:
- [math]\displaystyle{ f(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{\eta } \right)}^{\beta }}}} }[/math]
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] . The Eyring-Weibull model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}} }[/math]
or:
- [math]\displaystyle{ \frac{1}{\eta }=V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} }[/math]
Substituting for [math]\displaystyle{ \eta }[/math] into the Weibull [math]\displaystyle{ pdf }[/math] yields:
- [math]\displaystyle{ f(t,V)=\beta \cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}}{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}}{{e}^{-{{\left( t\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Eyring-Weibull Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T} }[/math], or Mean Time To Failure (MTTF) for the Eyring-Weibull model is given by:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right) }[/math]
where [math]\displaystyle{ \Gamma \left( \tfrac{1}{\beta }+1 \right) }[/math] is the gamma function evaluated at the value of [math]\displaystyle{ \left( \tfrac{1}{\beta }+1 \right) }[/math] .
Median
The median, [math]\displaystyle{ \breve{T} }[/math] for the Eyring-Weibull model is given by:
- [math]\displaystyle{ \breve{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}{{\left( \ln 2 \right)}^{\tfrac{1}{\beta }}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] for the Eyring-Weibull model is given by:
- [math]\displaystyle{ \tilde{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}{{\left( 1-\frac{1}{\beta } \right)}^{\tfrac{1}{\beta }}} }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}}, }[/math] for the Eyring-Weibull model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \sqrt{\Gamma \left( \frac{2}{\beta }+1 \right)-{{\left( \Gamma \left( \frac{1}{\beta }+1 \right) \right)}^{2}}} }[/math]
Eyring-Weibull Reliability Function
The Eyring-Weibull reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-{{\left( V\cdot T\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}} }[/math]
Conditional Reliability Function
The Eyring-Weibull conditional reliability function at a specified stress level is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-{{\left( \left( T+t \right)\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}}}{{{e}^{-{{\left( V\cdot T\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}}}} }[/math]
or:
- [math]\displaystyle{ R(T,t,V)={{e}^{-\left[ {{\left( \left( T+t \right)\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }}-{{\left( V\cdot T\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta }} \right]}} }[/math]
Reliable Life
For the Eyring-Weibull model, the reliable life, [math]\displaystyle{ {{t}_{R}} }[/math] , of a unit for a specified reliability and starting the mission at age zero is given by:
- [math]\displaystyle{ {{t}_{R}}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}{{\left\{ -\ln \left[ R\left( {{T}_{R}},V \right) \right] \right\}}^{\tfrac{1}{\beta }}} }[/math]
Eyring-Weibull Failure Rate Function
The Eyring-Weibull failure rate function, [math]\displaystyle{ \lambda (T) }[/math] , is given by:
- [math]\displaystyle{ \lambda \left( T,V \right)=\frac{f\left( T,V \right)}{R\left( T,V \right)}=\beta {{\left( T\cdot V\cdot {{e}^{\left( A-\tfrac{B}{V} \right)}} \right)}^{\beta -1}} }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The Eyring-Weibull log-likelihood function is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \beta \cdot {{V}_{i}}\cdot {{e}^{A-\tfrac{B}{{{V}_{i}}}}}{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta -1}}{{e}^{-{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( {{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}}T_{i}^{\prime } \right)}^{\beta }}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-{{\left( T_{Li}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-{{\left( T_{Ri}^{\prime \prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }}}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure data points in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ \beta }[/math] is the Weibull shape parameter (unknown, the first of three parameters to be estimated).
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the second of three parameters to be estimated).
• [math]\displaystyle{ B }[/math] is the second Eyring parameter (unknown, the third of three parameters to be estimated).
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the i [math]\displaystyle{ ^{th} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the i [math]\displaystyle{ ^{th} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the i [math]\displaystyle{ ^{th} }[/math] interval.
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \beta , }[/math] [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \beta }=0, }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math]
where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & \beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}-\beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} -\beta \underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( T_{i}^{\prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} \overset{FI}{\mathop{-\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\beta V_{i}^{\beta }{{e}^{A\beta -\tfrac{B\beta }{{{V}_{i}}}}}\left[ {{(T_{Li}^{\prime \prime })}^{\beta }}R_{Li}^{\prime \prime }-{{(T_{Ri}^{\prime \prime })}^{\beta }}R_{Ri}^{\prime \prime } \right]}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & -\beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}\frac{1}{{{V}_{i}}}+\beta \underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}\frac{1}{{{V}_{i}}}{{\left( {{T}_{i}}{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} +\beta \underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }\frac{1}{{{V}_{i}}}{{\left( T_{i}^{\prime }{{V}_{i}}{{e}^{A-\tfrac{B}{{{V}_{i}}}}} \right)}^{\beta }} +\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\beta V_{i}^{(\beta -1)}{{e}^{A\beta -\tfrac{B\beta }{{{V}_{i}}}}}\left[ {{(T_{Li}^{\prime \prime })}^{\beta }}R_{Li}^{\prime \prime }-{{(T_{Ri}^{\prime \prime })}^{\beta }}R_{Ri}^{\prime \prime } \right]}{R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda}{\partial \beta}= & \frac{1}{\beta}\sum_{i=1}^{F_e} N_i\frac{1}{V_i}+\sum_{i=1}^{F_e} N_i ln\left(T_iV_i e^{A-\tfrac{B}{V_i}}\right) -\sum_{i=1}^{F_e} N_i\left(T_iV_i e^{A-\tfrac{B}{V_i}}\right)^\beta ln\left(T_iV)i e^{A-\tfrac{B}{V_i}}\right)\\ & -\sum_{i=1}^S N_i^'\left(T_i^'V_I e^{A-\tfrac{B}{V_i}}\right)^\beta ln\left(T_iV)i e^{A-\tfrac{B}{V_i}}\right) -\sum_{i=1}^{FI} N_i^{''}V_i e^{A-\tfrac{B}{V_i}}\frac{R_{Li}^{''} T_{Li}^{''}\left(ln(T_{Li}^' V_i)+A-\tfrac{B}{V_i}\right)-R_{Ri}^{''} T_{Ri}^{''}\left(ln(T_{Ri}^{''} V_i)+A-\tfrac{B}{V_i}\right)}{R_{L_i}^{''}-F_{Ri}^{''}} \end{align} }[/math]
Consider the following times-to-failure data at three different stress levels.
The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding:
- [math]\displaystyle{ \widehat{\beta }=4.29186497\,\! }[/math]
- [math]\displaystyle{ \widehat{A}=-11.08784624\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1454.08635742\,\! }[/math]
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align}\,\! }[/math]
Eyring-Lognormal
The [math]\displaystyle{ pdf }[/math] of the lognormal distribution is given by:
- [math]\displaystyle{ f(T)=\frac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\overline{{{T}'}}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}} }[/math]
where:
- [math]\displaystyle{ {T}'=\ln (T) }[/math]
- [math]\displaystyle{ T=\text{times-to-failure} }[/math]
and
• [math]\displaystyle{ \overline{{{T}'}}= }[/math] mean of the natural logarithms of the times-to-failure.
• [math]\displaystyle{ {{\sigma }_{{{T}'}}}= }[/math] standard deviation of the natural logarithms of the times-to-failure.
The Eyring-lognormal model can be obtained first by setting [math]\displaystyle{ \breve{T}=L(V) }[/math]:
- [math]\displaystyle{ \breve{T}=L(V)=\frac{1}{V}{{e}^{-(A-\tfrac{B}{V})}} }[/math]
or:
- [math]\displaystyle{ {{e}^{{{\overline{T}}^{\prime }}}}=\frac{1}{V}{{e}^{-(A-\tfrac{B}{V})}} }[/math]
Thus:
- [math]\displaystyle{ {{\overline{T}}^{\prime }}=-\ln (V)-A+\frac{B}{V} }[/math]
Substituting this into the lognormal [math]\displaystyle{ pdf }[/math] yields the Eyring-lognormal model [math]\displaystyle{ pdf }[/math]:
- [math]\displaystyle{ f(T,V)=\frac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}} }[/math]
Eyring-Lognormal Statistical Properties Summary
The Mean
The mean life of the Eyring-lognormal model (mean of the times-to-failure), [math]\displaystyle{ \bar{T} }[/math] , is given by:
- [math]\displaystyle{ \begin{align} \bar{T}=\ {{e}^{\bar{{T}'}+\tfrac{1}{2}\sigma _{{{T}'}}^{2}}} =\ {{e}^{-\ln (V)-A+\tfrac{B}{V}+\tfrac{1}{2}\sigma _{{{T}'}}^{2}}} \end{align} }[/math]
The mean of the natural logarithms of the times-to-failure, [math]\displaystyle{ {{\bar{T}}^{^{\prime }}} }[/math] , in terms of [math]\displaystyle{ \bar{T} }[/math] and [math]\displaystyle{ {{\sigma }_{T}} }[/math] is given by:
- [math]\displaystyle{ {{\bar{T}}^{\prime }}=\ln \left( {\bar{T}} \right)-\frac{1}{2}\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right) }[/math]
The Median
The median of the Eyring-lognormal model is given by:
- [math]\displaystyle{ \breve{T}={{e}^{{{\overline{T}}^{\prime }}}} }[/math]
The Standard Deviation
The standard deviation of the Eyring-lognormal model (standard deviation of the times-to-failure), [math]\displaystyle{ {{\sigma }_{T}} }[/math] , is given by:
- [math]\displaystyle{ \begin{align} & {{\sigma }_{T}}= & \sqrt{\left( {{e}^{2\bar{{T}'}+\sigma _{{{T}'}}^{2}}} \right)\left( {{e}^{\sigma _{{{T}'}}^{2}}}-1 \right)} =\ \sqrt{\left( {{e}^{2\left( -\ln (V)-A+\tfrac{B}{V} \right)+\sigma _{{{T}'}}^{2}}} \right)\left( {{e}^{\sigma _{{{T}'}}^{2}}}-1 \right)} \end{align} }[/math]
The standard deviation of the natural logarithms of the times-to-failure, [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] , in terms of [math]\displaystyle{ \bar{T} }[/math] and [math]\displaystyle{ {{\sigma }_{T}} }[/math] is given by:
- [math]\displaystyle{ {{\sigma }_{{{T}'}}}=\sqrt{\ln \left( \frac{\sigma _{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)} }[/math]
The Mode
The mode of the Eyring-lognormal model is given by:
- [math]\displaystyle{ \begin{align} & \tilde{T}= & {{e}^{{{\overline{T}}^{\prime }}-\sigma _{{{T}'}}^{2}}} =\ {{e}^{-\ln (V)-A+\tfrac{B}{V}-\sigma _{{{T}'}}^{2}}} \end{align} }[/math]
Eyring-Lognormal Reliability Function
The reliability for a mission of time [math]\displaystyle{ T }[/math] , starting at age 0, for the Eyring-lognormal model is determined by:
- [math]\displaystyle{ R(T,V)=\int_{T}^{\infty }f(t,V)dt }[/math]
or:
- [math]\displaystyle{ R(T,V)=\int_{{{T}^{^{\prime }}}}^{\infty }\frac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}dt }[/math]
There is no closed form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability we will not discuss manual solution methods.
Reliable Life
For the Eyring-lognormal model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}, }[/math] is estimated by first solving the reliability equation with respect to time, as follows:
- [math]\displaystyle{ T_{R}^{\prime }=-\ln (V)-A+\frac{B}{V}+z\cdot {{\sigma }_{{{T}'}}} }[/math]
where:
- [math]\displaystyle{ z={{\Phi }^{-1}}\left[ F\left( T_{R}^{\prime },V \right) \right] }[/math]
and:
- [math]\displaystyle{ \Phi (z)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{z({T}',V)}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt }[/math]
Since [math]\displaystyle{ {T}'=\ln (T) }[/math] the reliable life, [math]\displaystyle{ {{t}_{R,}} }[/math] is given by:
- [math]\displaystyle{ {{t}_{R}}={{e}^{T_{R}^{\prime }}} }[/math]
Eyring-Lognormal Failure Rate
The Eyring-lognormal failure rate is given by:
- [math]\displaystyle{ \lambda (T,V)=\frac{f(T,V)}{R(T,V)}=\frac{\tfrac{1}{T\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}}{\int_{{{T}'}}^{\infty }\tfrac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'+\ln (V)+A-\tfrac{B}{V}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}}dt} }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The complete Eyring-lognormal log-likelihood function is composed of two summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{{{\sigma }_{{{T}'}}}{{T}_{i}}}\phi \left( \frac{\ln \left( {{T}_{i}} \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right) \right] \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ 1-\Phi \left( \frac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right) \right] +\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]
where:
- [math]\displaystyle{ z_{Li}^{\prime \prime }=\frac{\ln T_{Li}^{\prime \prime }+\ln {{V}_{i}}+A-\tfrac{B}{{{V}_{i}}}}{\sigma _{T}^{\prime }} }[/math]
- [math]\displaystyle{ z_{Ri}^{\prime \prime }=\frac{\ln T_{Ri}^{\prime \prime }+\ln {{V}_{i}}+A-\tfrac{B}{{{V}_{i}}}}{\sigma _{T}^{\prime }} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure data points in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] is the standard deviation of the natural logarithm of the times-to-failure (unknown, the first of three parameters to be estimated).
• [math]\displaystyle{ A }[/math] is the Eyring parameter (unknown, the second of three parameters to be estimated).
• [math]\displaystyle{ C }[/math] is the second Eyring parameter (unknown, the third of three parameters to be estimated).
• [math]\displaystyle{ {{V}_{i}} }[/math] is the stress level of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the i [math]\displaystyle{ ^{th} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
The solution (parameter estimates) will be found by solving for [math]\displaystyle{ {{\widehat{\sigma }}_{{{T}'}}}, }[/math] [math]\displaystyle{ \widehat{A}, }[/math] [math]\displaystyle{ \widehat{B} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}=0, }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial A}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] :
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial A}= & -\frac{1}{\sigma _{{{T}'}}^{2}}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}(\ln ({{T}_{i}})+\ln ({{V}_{i}})+A-\frac{B}{{{V}_{i}}}) -\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)} \overset{FI}{\mathop{+\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\varphi (z_{Ri}^{\prime \prime })-\varphi (z_{Li}^{\prime \prime })}{\sigma _{T}^{\prime }(\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime }))} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= \frac{1}{\sigma _{{{T}'}}^{2}}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\frac{1}{{{V}_{i}}}(\ln ({{T}_{i}})+\ln ({{V}_{i}})+A-\frac{B}{{{V}_{i}}}) +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{1}{{{V}_{i}}}\frac{\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)} \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{\varphi (z_{Ri}^{\prime \prime })-\varphi (z_{Li}^{\prime \prime })}{\sigma _{T}^{\prime }{{V}_{i}}(\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime }))} \\ & \frac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}= \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{\left( \ln ({{T}_{i}})+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}} \right)}^{2}}}{\sigma _{{{T}'}}^{3}}-\frac{1}{{{\sigma }_{{{T}'}}}} \right) +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)+\ln ({{V}_{i}})+A-\tfrac{B}{{{V}_{i}}}}{{{\sigma }_{{{T}'}}}} \right)} \overset{FI}{\mathop{\underset{i=1}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{z_{Ri}^{\prime \prime }\varphi (z_{Ri}^{\prime \prime })-z_{Li}^{\prime \prime }\varphi (z_{Li}^{\prime \prime })}{\sigma _{T}^{\prime }(\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime }))} \end{align} }[/math]
and:
- [math]\displaystyle{ \phi \left( x \right)=\frac{1}{\sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( x \right)}^{2}}}} }[/math]
- [math]\displaystyle{ \Phi (x)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt }[/math]
Template loop detected: Template:Generalized eyring
Template loop detected: Template:Eyring confidence bounds