Template:Example: Lognormal Distribution Likelihood Ratio Bound (Reliability)

Lognormal Distribution Likelihood Ratio Bound Example (Reliability)

For the data given in Example 5, determine the two-sided 75% confidence bounds on the reliability estimate for [math]\displaystyle{ t=65 }[/math] . The ML estimate for the reliability at [math]\displaystyle{ t=65 }[/math] is 64.261%.

Solution

In this example, we are trying to determine the two-sided 75% confidence bounds on the reliability estimate of 64.261%. This is accomplished by substituting [math]\displaystyle{ t=65 }[/math] and [math]\displaystyle{ \alpha =0.75 }[/math] into the likelihood function, and varying [math]\displaystyle{ {{\sigma'}} }[/math] until the maximum and minimum values of [math]\displaystyle{ R }[/math] are found. The following table gives the values of [math]\displaystyle{ R }[/math] based on given values of [math]\displaystyle{ {{\sigma' }} }[/math] .

[math]\displaystyle{ \begin{matrix} {{\sigma'}} & {{R}_{1}} & {{R}_{2}} & {{\sigma'}} & {{R}_{1}} & {{R}_{2}} \\ 0.24 & 61.107% & 75.910% & 0.37 & 43.573% & 78.845% \\ 0.25 & 55.906% & 78.742% & 0.38 & 43.807% & 78.180% \\ 0.26 & 55.528% & 80.131% & 0.39 & 44.147% & 77.448% \\ 0.27 & 50.067% & 80.903% & 0.40 & 44.593% & 76.646% \\ 0.28 & 48.206% & 81.319% & 0.41 & 45.146% & 75.767% \\ 0.29 & 46.779% & 81.499% & 0.42 & 45.813% & 74.802% \\ 0.30 & 45.685% & 81.508% & 0.43 & 46.604% & 73.737% \\ 0.31 & 44.857% & 81.387% & 0.44 & 47.538% & 72.551% \\ 0.32 & 44.250% & 81.159% & 0.45 & 48.645% & 71.212% \\ 0.33 & 43.827% & 80.842% & 0.46 & 49.980% & 69.661% \\ 0.34 & 43.565% & 80.446% & 0.47 & 51.652% & 67.789% \\ 0.35 & 43.444% & 79.979% & 0.48 & 53.956% & 65.299% \\ 0.36 & 43.450% & 79.444% & {} & {} & {} \\ \end{matrix} }[/math]

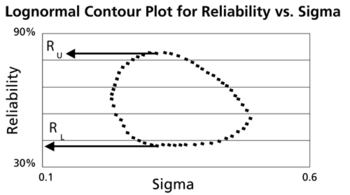
This data set is represented graphically in the following contour plot:

As can be determined from the table, the lowest calculated value for [math]\displaystyle{ R }[/math] is 43.444%, while the highest is 81.508%. These represent the two-sided 75% confidence limits on the reliability at [math]\displaystyle{ t=65 }[/math] .