Inverse Power Law Relationship

Introduction

The inverse power law (IPL) model (or relationship) is commonly used for non-thermal accelerated stresses and is given by:

[math]\displaystyle{ L(V)=\frac{1}{K{{V}^{n}}} }[/math]

where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.

• [math]\displaystyle{ V }[/math] represents the stress level.

• [math]\displaystyle{ K }[/math] is one of the model parameters to be determined, [math]\displaystyle{ (K\gt 0). }[/math]

• [math]\displaystyle{ n }[/math] is another model parameter to be determined.

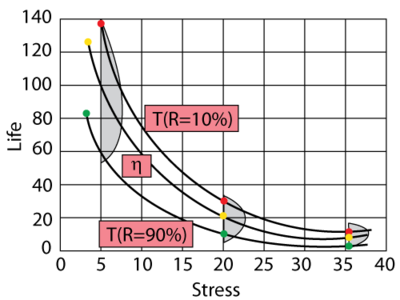
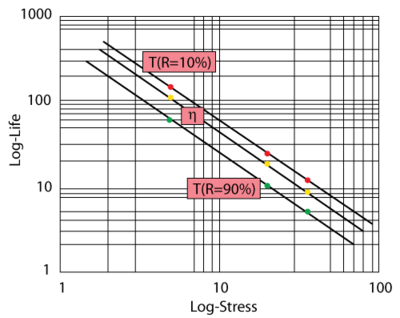
The inverse power law appears as a straight line when plotted on a log-log paper. The equation of the line is given by:

[math]\displaystyle{ \ln (L)=-\ln (K)-n\ln (V) }[/math]

Plotting methods are widely used in estimating the parameters of the inverse power law relationship since obtaining [math]\displaystyle{ K }[/math] and [math]\displaystyle{ n }[/math] is as simple as finding the slope and the intercept in the above equation.

A Look at the Parameter [math]\displaystyle{ n }[/math]

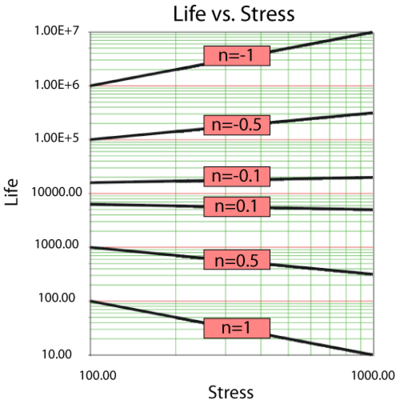
The parameter [math]\displaystyle{ n }[/math] in the inverse power relationship is a measure of the effect of the stress on the life. As the absolute value of [math]\displaystyle{ n }[/math] increases, the greater the effect of the stress. Negative values of [math]\displaystyle{ n }[/math] indicate an increasing life with increasing stress. An absolute value of [math]\displaystyle{ n }[/math] approaching zero indicates small effect of the stress on the life, with no effect (constant life with stress) when [math]\displaystyle{ n=0. }[/math]

Acceleration Factor=

For the IPL relationship the acceleration factor is given by:

[math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{KV_{u}^{n}}}{\tfrac{1}{KV_{A}^{n}}}={{\left( \frac{{{V}_{A}}}{{{V}_{u}}} \right)}^{n}} }[/math]

where:
• [math]\displaystyle{ {{L}_{USE}} }[/math] is the life at use stress level.

• [math]\displaystyle{ {{L}_{Accelerated}} }[/math] is the life at the accelerated stress level.

• [math]\displaystyle{ {{V}_{u}} }[/math] is the use stress level.

• [math]\displaystyle{ {{V}_{A}} }[/math] is the accelerated stress level.

Introduction

The inverse power law (IPL) model (or relationship) is commonly used for non-thermal accelerated stresses and is given by:

[math]\displaystyle{ L(V)=\frac{1}{K{{V}^{n}}} }[/math]

where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.

• [math]\displaystyle{ V }[/math] represents the stress level.

• [math]\displaystyle{ K }[/math] is one of the model parameters to be determined, [math]\displaystyle{ (K\gt 0). }[/math]

• [math]\displaystyle{ n }[/math] is another model parameter to be determined.

The inverse power law appears as a straight line when plotted on a log-log paper. The equation of the line is given by:

[math]\displaystyle{ \ln (L)=-\ln (K)-n\ln (V) }[/math]

Plotting methods are widely used in estimating the parameters of the inverse power law relationship since obtaining [math]\displaystyle{ K }[/math] and [math]\displaystyle{ n }[/math] is as simple as finding the slope and the intercept in the above equation.

A Look at the Parameter [math]\displaystyle{ n }[/math]

The parameter [math]\displaystyle{ n }[/math] in the inverse power relationship is a measure of the effect of the stress on the life. As the absolute value of [math]\displaystyle{ n }[/math] increases, the greater the effect of the stress. Negative values of [math]\displaystyle{ n }[/math] indicate an increasing life with increasing stress. An absolute value of [math]\displaystyle{ n }[/math] approaching zero indicates small effect of the stress on the life, with no effect (constant life with stress) when [math]\displaystyle{ n=0. }[/math]

Acceleration Factor=

For the IPL relationship the acceleration factor is given by:

[math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{KV_{u}^{n}}}{\tfrac{1}{KV_{A}^{n}}}={{\left( \frac{{{V}_{A}}}{{{V}_{u}}} \right)}^{n}} }[/math]

where:
• [math]\displaystyle{ {{L}_{USE}} }[/math] is the life at use stress level.

• [math]\displaystyle{ {{L}_{Accelerated}} }[/math] is the life at the accelerated stress level.

• [math]\displaystyle{ {{V}_{u}} }[/math] is the use stress level.

• [math]\displaystyle{ {{V}_{A}} }[/math] is the accelerated stress level.

Consider the following times-to-failure data at two different stress levels.

The data set was analyzed jointly in an ALTA standard folio using the IPL-Weibull model, with a complete MLE solution over the entire data set. The analysis yields:

[math]\displaystyle{ \widehat{\beta }=2.616464\,\! }[/math]

[math]\displaystyle{ \widehat{K}=0.001022\,\! }[/math]

[math]\displaystyle{ \widehat{n}=1.327292\,\! }[/math]

IPL and the Coffin-Manson Relationship

In accelerated life testing analysis, thermal cycling is commonly treated as a low-cycle fatigue problem, using the inverse power law relationship. Coffin and Manson suggested that the number of cycles-to-failure of a metal subjected to thermal cycling is given by [28]:

[math]\displaystyle{ N=\frac{C}{{{\left( \Delta T \right)}^{\gamma }}} }[/math]

where:
• [math]\displaystyle{ N }[/math] is the number of cycles to failure.
• [math]\displaystyle{ C }[/math] is a constant, characteristic of the metal.
• [math]\displaystyle{ \gamma }[/math] is another constant, also characteristic of the metal.
• [math]\displaystyle{ \Delta T }[/math] is the range of the thermal cycle.

This relationship is basically the inverse power law relationship, where the stress [math]\displaystyle{ V, }[/math] is substituted by the range [math]\displaystyle{ \Delta V }[/math]. This is an attempt to simplify the analysis of a time-varying stress test by using a constant stress model. It is a very commonly used methodology for thermal cycling and mechanical fatigue tests. However, by performing such a simplification, the following assumptions and shortcomings are inevitable. First, the acceleration effects due to the stress rate of change are ignored. In other words, it is assumed that the failures are accelerated by the stress difference and not by how rapidly this difference occurs. Secondly, the acceleration effects due to stress relaxation and creep are ignored.

Example
In this example the use of the Coffin-Manson relationship will be illustrated. This is a very simple example which can be repeated at any time. The reader is encouraged to perform this test.

Product: ACME Paper Clip Model 4456
Reliability Target: 99% at a 90% confidence after 30 cycles of 45º

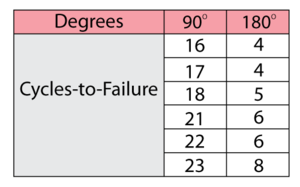
After consulting with our paper-clip engineers, the acceleration stress was determined to be the angle to which the clips are bent. Two bend stresses of 90º and 180º were used. A sample of six paper clips was tested to failure at both 90º and 180º bends with the following data obtained.

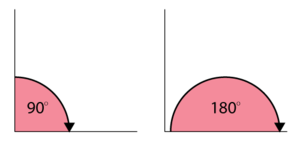
The test was performed as shown in the next figures (a side-view of the paper-clip is shown).

Using the IPL-lognormal model, determine whether the reliability target was met.


Solution
By using the IPL relationship to analyze the data, we are actually using a constant stress model to analyze a cycling process. Caution must be exercised when performing the test. The rate of change in the angle must be constant and equal for both the 90º and 180º bends and constant and equal to the rate of change in the angle for the use life of 45º bend. Rate effects are influencing the life of the paper clip. By keeping the rate constant and equal at all stress levels, we can then eliminate these rate effects from our analysis. Otherwise the analysis will not be valid.

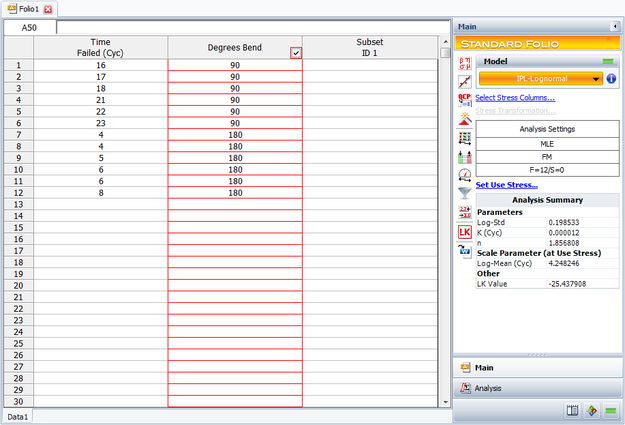
The data were entered and analyzed using ReliaSoft's ALTA.

The parameters of the IPL-lognormal model were estimated to be:

[math]\displaystyle{ \begin{align} & \sigma = & 0.198533 \\ & K= & 0.000012 \\ & n= & 1.856808 \end{align} }[/math]

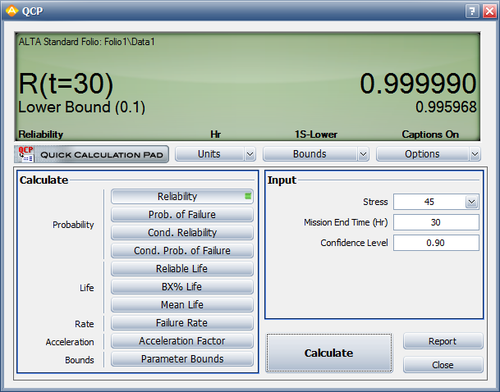
Using the QCP, the 90% lower 1-sided confidence bound on reliability after 30 cycles for a 45º bend was estimated to be [math]\displaystyle{ 99.6% }[/math] , as shown below.

This meets the target reliability of 99%.

IPL Confidence Bounds

Approximate Confidence Bounds on IPL-Exponential

Confidence Bounds on the Mean Life

From the inverse power law relationship the mean life for the exponential distribution is given by setting [math]\displaystyle{ m=L(V) }[/math] . The upper [math]\displaystyle{ ({{m}_{U}}) }[/math] and lower [math]\displaystyle{ ({{m}_{L}}) }[/math] bounds on the mean life (ML estimate of the mean life) are estimated by:

[math]\displaystyle{ {{m}_{U}}=\widehat{m}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}} }[/math]

[math]\displaystyle{ {{m}_{L}}=\widehat{m}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}} }[/math]

where [math]\displaystyle{ {{K}_{\alpha }} }[/math] is defined by:

[math]\displaystyle{ \alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }}) }[/math]

If [math]\displaystyle{ \delta }[/math] is the confidence level, then [math]\displaystyle{ \alpha =\tfrac{1-\delta }{2} }[/math] for the two-sided bounds, and [math]\displaystyle{ \alpha =1-\delta }[/math] for the one-sided bounds. The variance of [math]\displaystyle{ \widehat{m} }[/math] is given by:

[math]\displaystyle{ \begin{align} & Var(\widehat{m})= & {{\left( \frac{\partial m}{\partial K} \right)}^{2}}Var(\widehat{K})+{{\left( \frac{\partial m}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial m}{\partial K} \right)\left( \frac{\partial m}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ Var(\widehat{m})=\frac{1}{{{\widehat{K}}^{2}}{{V}^{2\widehat{n}}}}\left[ \frac{1}{{{\widehat{K}}^{2}}}Var(\widehat{K})+{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n})+\frac{2\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \right] }[/math]

The variances and covariance of [math]\displaystyle{ K }[/math] and [math]\displaystyle{ n }[/math] are estimated from the Fisher matrix (evaluated at [math]\displaystyle{ \widehat{K}, }[/math] [math]\displaystyle{ \widehat{n}) }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov(\widehat{n},\widehat{K}) & Var(\widehat{n}) \\ \end{matrix} \right]={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right]}^{-1}} }[/math]

Confidence Bounds on Reliability

The bounds on reliability at a given time, [math]\displaystyle{ T }[/math] , are estimated by:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & {{e}^{-\tfrac{T}{{{m}_{U}}}}} \\ & {{R}_{L}}= & {{e}^{-\tfrac{T}{{{m}_{L}}}}} \end{align} }[/math]

Confidence Bounds on Time

The bounds on time (ML estimate of time) for a given reliability are estimated by first solving the reliability function with respect to time:

[math]\displaystyle{ \widehat{T}=-\widehat{m}\cdot \ln (R) }[/math]

The corresponding confidence bounds are estimated from:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & -{{m}_{U}}\cdot \ln (R) \\ & {{T}_{L}}= & -{{m}_{L}}\cdot \ln (R) \end{align} }[/math]

Approximate Confidence Bounds on IPL-Weibull

Bounds on the Parameters

Using the same approach as previously discussed ( [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{K} }[/math] positive parameters):

[math]\displaystyle{ \begin{align} & {{\beta }_{U}}= & \widehat{\beta }\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}} \\ & {{\beta }_{L}}= & \widehat{\beta }\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}} \end{align} }[/math]

[math]\displaystyle{ \begin{align} & {{K}_{U}}= & \widehat{K}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} \\ & {{K}_{L}}= & \widehat{K}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} & {{n}_{U}}= & \widehat{n}+{{K}_{\alpha }}\sqrt{Var(\widehat{n})} \\ & {{n}_{L}}= & \widehat{n}-{{K}_{\alpha }}\sqrt{Var(\widehat{n})} \end{align} }[/math]

The variances and covariances of [math]\displaystyle{ \beta , }[/math] [math]\displaystyle{ K, }[/math] and [math]\displaystyle{ n }[/math] are estimated from the local Fisher matrix (evaluated at [math]\displaystyle{ \widehat{\beta }, }[/math] [math]\displaystyle{ \widehat{K}, }[/math] [math]\displaystyle{ \widehat{n}) }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var(\widehat{\beta }) & Cov(\widehat{\beta },\widehat{K}) & Cov(\widehat{\beta },\widehat{n}) \\ Cov(\widehat{K},\widehat{\beta }) & Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov(\widehat{n},\widehat{\beta }) & Cov(\widehat{n},\widehat{K}) & Var(\widehat{n}) \\ \end{matrix} \right]={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\beta }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right]}^{-1}} }[/math]

Confidence Bounds on Reliability

The reliability function (ML estimate) for the IPL-Weibull model is given by:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-{{\left( \widehat{K}{{V}^{\widehat{n}}}T \right)}^{\widehat{\beta }}}}} }[/math]

or:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-{{e}^{\ln \left[ {{\left( \widehat{K}{{V}^{\widehat{n}}}T \right)}^{\widehat{\beta }}} \right]}}}} }[/math]

Setting:

[math]\displaystyle{ \widehat{u}=\ln \left[ \left( \widehat{K}V\widehat{^{n}}T \right)\widehat{^{\beta }} \right] }[/math]

or:

[math]\displaystyle{ \widehat{u}=\widehat{\beta }\left[ \ln (T)+\ln (\widehat{K})+\widehat{n}\ln (V) \right] }[/math]

The reliability function now becomes:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-e\widehat{^{u}}}} }[/math]

The next step is to find the upper and lower bounds on [math]\displaystyle{ \widehat{u} }[/math] :

[math]\displaystyle{ {{u}_{U}}=\widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

[math]\displaystyle{ {{u}_{L}}=\widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

where:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial K} \right)}^{2}}Var(\widehat{K}) +{{\left( \frac{\partial \widehat{u}}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial K} \right)Cov(\widehat{\beta },\widehat{K})\\ & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{\beta },\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial K} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{u})= & {{\left( \frac{\widehat{u}}{\widehat{\beta }} \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\widehat{\beta }}{\widehat{K}} \right)}^{2}}Var(\widehat{K}) +{{\widehat{\beta }}^{2}}{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n}) +\frac{2\widehat{u}}{\widehat{K}}Cov(\widehat{\beta },\widehat{K})+2\widehat{u}\ln (V)Cov(\widehat{\beta },\widehat{n})+\frac{2{{\widehat{\beta }}^{2}}\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & {{e}^{-{{e}^{\left( {{u}_{L}} \right)}}}} \\ & {{R}_{L}}= & {{e}^{-{{e}^{\left( {{u}_{U}} \right)}}}} \end{align} }[/math]

Confidence Bounds on Time

The bounds on time for a given reliability (ML estimate of time) are estimated by first solving the reliability function with respect to time:

[math]\displaystyle{ \begin{align} \ln (R) &=\ -{{\left( \widehat{K}{{V}^{\widehat{n}}}\widehat{T} \right)}^{\widehat{\beta }}} \\ \ln (-\ln (R)) &=\ \widehat{\beta }\left[ \ln (\widehat{T})+\ln (\widehat{K})+\widehat{n}\ln (V) \right] \end{align} }[/math]

or:

[math]\displaystyle{ \widehat{u}=\frac{1}{\widehat{\beta }}\ln (-\ln (R))-\ln (\widehat{K})-\widehat{n}\ln (V) }[/math]

where [math]\displaystyle{ \widehat{u}=\ln \widehat{T}. }[/math] The upper and lower bounds on [math]\displaystyle{ u }[/math] are estimated from:

[math]\displaystyle{ \begin{align} & {{u}_{U}}= & \widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})} \\ & {{u}_{L}}= & \widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})} \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial K} \right)}^{2}}Var(\widehat{K}) +{{\left( \frac{\partial \widehat{u}}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial K} \right)Cov(\widehat{\beta },\widehat{K}) \\ & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{\beta },\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial K} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & \frac{1}{{{\widehat{\beta }}^{4}}}{{\left[ \ln (-\ln (R)) \right]}^{2}}Var(\widehat{\beta })+\frac{1}{{{\widehat{K}}^{2}}}Var(\widehat{K}) +{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n}) +\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}\widehat{K}}Cov(\widehat{\beta },\widehat{K}) \\ & +\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}}\ln (V)Cov(\widehat{\beta },\widehat{n}) +\frac{2\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

The upper and lower bounds on time are then found by:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & {{e}^{{{u}_{U}}}} \\ & {{T}_{L}}= & {{e}^{{{u}_{L}}}} \end{align} }[/math]

Approximate Confidence Bounds on IPL-Lognormal

Bounds on the Parameters

Since the standard deviation, [math]\displaystyle{ {{\widehat{\sigma }}_{T}} }[/math] , and [math]\displaystyle{ \widehat{K} }[/math] are positive parameters, then [math]\displaystyle{ \ln ({{\widehat{\sigma }}_{{{T}'}}}) }[/math] and [math]\displaystyle{ \ln (\widehat{K}) }[/math] are treated as normally distributed, and the bounds are estimated from:

[math]\displaystyle{ \begin{align} {{\sigma }_{U}}=\ & {{\widehat{\sigma }}_{{{T}'}}}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}} &\text{ (Upper bound)} \\ {{\sigma }_{L}}=\ & \frac{{{\widehat{\sigma }}_{{{T}'}}}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}}} &\text{ (Lower bound)} \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} {{K}_{U}}=\ & \widehat{K}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} &\text{ (Upper bound)} \\ {{K}_{L}}=\ & \frac{\widehat{K}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}}} &\text{ (Lower bound)} \end{align} }[/math]

The lower and upper bounds on [math]\displaystyle{ n }[/math] , are estimated from:

[math]\displaystyle{ \begin{align} & {{n}_{U}}= & \widehat{n}+{{K}_{\alpha }}\sqrt{Var(\widehat{n})}\text{ (Upper bound)} \\ & {{n}_{L}}= & \widehat{n}-{{K}_{\alpha }}\sqrt{Var(\widehat{n})}\text{ (Lower bound)} \end{align} }[/math]

The variances and covariances of [math]\displaystyle{ A, }[/math] [math]\displaystyle{ B, }[/math] and [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] are estimated from the local Fisher matrix (evaluated at [math]\displaystyle{ \widehat{A}, }[/math] [math]\displaystyle{ \widehat{B} }[/math] , [math]\displaystyle{ {{\widehat{\sigma }}_{{{T}'}}}), }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var({{\widehat{\sigma }}_{{{T}'}}}) & Cov(\widehat{K},{{\widehat{\sigma }}_{{{T}'}}}) & Cov(\widehat{n},{{\widehat{\sigma }}_{{{T}'}}}) \\ Cov({{\widehat{\sigma }}_{{{T}'}}},\widehat{K}) & Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov({{\widehat{\sigma }}_{{{T}'}}},\widehat{n}) & Cov(\widehat{n},\widehat{K}) & Var\left( \widehat{n} \right) \\ \end{matrix} \right]={{\left[ F \right]}^{-1}} }[/math]

where:

[math]\displaystyle{ F=\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial \sigma _{{{T}'}}^{2}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right] }[/math]

Bounds on Reliability

The reliability of the lognormal distribution is:

[math]\displaystyle{ R({T}',V;K,n,{{\sigma }_{{{T}'}}})=\int_{{{T}'}}^{\infty }\frac{1}{{{\widehat{\sigma }}_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}} \right)}^{2}}}}dt }[/math]

Let [math]\displaystyle{ \widehat{z}(t,V;K,n,{{\sigma }_{T}})=\tfrac{t+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}}, }[/math] then [math]\displaystyle{ \tfrac{d\widehat{z}}{dt}=\tfrac{1}{{{\widehat{\sigma }}_{{{T}'}}}}. }[/math]

For [math]\displaystyle{ t={T}' }[/math] , [math]\displaystyle{ \widehat{z}=\tfrac{{T}'+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}} }[/math] , and for [math]\displaystyle{ t=\infty , }[/math] [math]\displaystyle{ \widehat{z}=\infty . }[/math] The above equation then becomes:

[math]\displaystyle{ R(\widehat{z})=\int_{\widehat{z}({T}',V)}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz }[/math]

The bounds on [math]\displaystyle{ z }[/math] are estimated from:

[math]\displaystyle{ \begin{align} & {{z}_{U}}= & \widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \\ & {{z}_{L}}= & \widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \end{align} }[/math]

where:

.

[math]\displaystyle{ \begin{align} Var(\widehat{z})= & \left( \frac{\partial \widehat{z}}{\partial K} \right)_{\widehat{K}}^{2}Var(\widehat{K})+\left( \frac{\partial \widehat{z}}{\partial n} \right)_{\widehat{n}}^{2}Var(\widehat{n})+\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)_{{{\widehat{\sigma }}_{{{T}'}}}}^{2}Var({{\widehat{\sigma }}_{T}}) +2{{\left( \frac{\partial \widehat{z}}{\partial K} \right)}_{\widehat{K}}}{{\left( \frac{\partial \widehat{z}}{\partial n} \right)}_{\widehat{n}}}Cov\left( \widehat{K},\widehat{n} \right) \\ & +2{{\left( \frac{\partial \widehat{z}}{\partial K} \right)}_{\widehat{K}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{K},{{\widehat{\sigma }}_{T}} \right) +2{{\left( \frac{\partial \widehat{z}}{\partial n} \right)}_{\widehat{n}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{n},{{\widehat{\sigma }}_{T}} \right) \end{align} }[/math].

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{z})= & \frac{1}{\widehat{\sigma }_{{{T}'}}^{2}}[\frac{1}{{{K}^{2}}}Var(\widehat{K})+\ln {{(V)}^{2}}Var(\widehat{n})+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +\frac{2\ln (V)}{K}Cov\left( \widehat{K},\widehat{n} \right)-\frac{2\widehat{z}}{K}Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right)-2\widehat{z}\ln (V)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right)] \end{align} }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & \int_{{{z}_{L}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Upper bound)} \\ & {{R}_{L}}= & \int_{{{z}_{U}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Lower bound)} \end{align} }[/math]

Confidence Bounds on Time

The bounds around time, for a given lognormal percentile (unreliability), are estimated by first solving the reliability equation with respect to time, as follows:

[math]\displaystyle{ {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}})=-\ln (\widehat{K})-\widehat{n}\ln (V)+z\cdot {{\widehat{\sigma }}_{{{T}'}}} }[/math]

where:

[math]\displaystyle{ \begin{align} & {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}})=\ \ln (T) \\ \\ & z=\ {{\Phi }^{-1}}\left[ F({T}') \right] \end{align} }[/math]

and:

[math]\displaystyle{ \Phi (z)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{z({T}')}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz }[/math]

The next step is to calculate the variance of [math]\displaystyle{ {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}}): }[/math]

[math]\displaystyle{ \begin{align} Var({T}')= & {{\left( \frac{\partial {T}'}{\partial K} \right)}^{2}}Var(\widehat{K})+{{\left( \frac{\partial {T}'}{\partial n} \right)}^{2}}Var(\widehat{n})+{{\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +2\left( \frac{\partial {T}'}{\partial K} \right)\left( \frac{\partial {T}'}{\partial n} \right)Cov\left( \widehat{K},\widehat{n} \right) \\ & +2\left( \frac{\partial {T}'}{\partial K} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right) +2\left( \frac{\partial {T}'}{\partial n} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} Var({T}')= & \frac{1}{{{K}^{2}}}Var(\widehat{K})+\ln {{(V)}^{2}}Var(\widehat{n})+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +\frac{2\ln (V)}{K}Cov\left( \widehat{K},\widehat{n} \right) \\ & -\frac{2\widehat{z}}{K}Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right) -2\widehat{z}\ln (V)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) \end{align} }[/math]

The upper and lower bounds are then found by:

[math]\displaystyle{ \begin{align} & T_{U}^{\prime }= & \ln {{T}_{U}}={T}'+{{K}_{\alpha }}\sqrt{Var({T}')} \\ & T_{L}^{\prime }= & \ln {{T}_{L}}={T}'-{{K}_{\alpha }}\sqrt{Var({T}')} \end{align} }[/math]

Solving for [math]\displaystyle{ {{T}_{U}} }[/math] and [math]\displaystyle{ {{T}_{L}} }[/math] yields:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & {{e}^{T_{U}^{\prime }}}\text{ (Upper bound)} \\ & {{T}_{L}}= & {{e}^{T_{L}^{\prime }}}\text{ (Lower bound)} \end{align} }[/math]

Introduction

The inverse power law (IPL) model (or relationship) is commonly used for non-thermal accelerated stresses and is given by:

[math]\displaystyle{ L(V)=\frac{1}{K{{V}^{n}}} }[/math]

where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.

• [math]\displaystyle{ V }[/math] represents the stress level.

• [math]\displaystyle{ K }[/math] is one of the model parameters to be determined, [math]\displaystyle{ (K\gt 0). }[/math]

• [math]\displaystyle{ n }[/math] is another model parameter to be determined.

The inverse power law appears as a straight line when plotted on a log-log paper. The equation of the line is given by:

[math]\displaystyle{ \ln (L)=-\ln (K)-n\ln (V) }[/math]

Plotting methods are widely used in estimating the parameters of the inverse power law relationship since obtaining [math]\displaystyle{ K }[/math] and [math]\displaystyle{ n }[/math] is as simple as finding the slope and the intercept in the above equation.

A Look at the Parameter [math]\displaystyle{ n }[/math]

The parameter [math]\displaystyle{ n }[/math] in the inverse power relationship is a measure of the effect of the stress on the life. As the absolute value of [math]\displaystyle{ n }[/math] increases, the greater the effect of the stress. Negative values of [math]\displaystyle{ n }[/math] indicate an increasing life with increasing stress. An absolute value of [math]\displaystyle{ n }[/math] approaching zero indicates small effect of the stress on the life, with no effect (constant life with stress) when [math]\displaystyle{ n=0. }[/math]

Acceleration Factor=

For the IPL relationship the acceleration factor is given by:

[math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{KV_{u}^{n}}}{\tfrac{1}{KV_{A}^{n}}}={{\left( \frac{{{V}_{A}}}{{{V}_{u}}} \right)}^{n}} }[/math]

where:
• [math]\displaystyle{ {{L}_{USE}} }[/math] is the life at use stress level.

• [math]\displaystyle{ {{L}_{Accelerated}} }[/math] is the life at the accelerated stress level.

• [math]\displaystyle{ {{V}_{u}} }[/math] is the use stress level.

• [math]\displaystyle{ {{V}_{A}} }[/math] is the accelerated stress level.

Consider the following times-to-failure data at two different stress levels.

The data set was analyzed jointly in an ALTA standard folio using the IPL-Weibull model, with a complete MLE solution over the entire data set. The analysis yields:

[math]\displaystyle{ \widehat{\beta }=2.616464\,\! }[/math]

[math]\displaystyle{ \widehat{K}=0.001022\,\! }[/math]

[math]\displaystyle{ \widehat{n}=1.327292\,\! }[/math]

IPL and the Coffin-Manson Relationship

In accelerated life testing analysis, thermal cycling is commonly treated as a low-cycle fatigue problem, using the inverse power law relationship. Coffin and Manson suggested that the number of cycles-to-failure of a metal subjected to thermal cycling is given by [28]:

[math]\displaystyle{ N=\frac{C}{{{\left( \Delta T \right)}^{\gamma }}} }[/math]

where:
• [math]\displaystyle{ N }[/math] is the number of cycles to failure.
• [math]\displaystyle{ C }[/math] is a constant, characteristic of the metal.
• [math]\displaystyle{ \gamma }[/math] is another constant, also characteristic of the metal.
• [math]\displaystyle{ \Delta T }[/math] is the range of the thermal cycle.

This relationship is basically the inverse power law relationship, where the stress [math]\displaystyle{ V, }[/math] is substituted by the range [math]\displaystyle{ \Delta V }[/math]. This is an attempt to simplify the analysis of a time-varying stress test by using a constant stress model. It is a very commonly used methodology for thermal cycling and mechanical fatigue tests. However, by performing such a simplification, the following assumptions and shortcomings are inevitable. First, the acceleration effects due to the stress rate of change are ignored. In other words, it is assumed that the failures are accelerated by the stress difference and not by how rapidly this difference occurs. Secondly, the acceleration effects due to stress relaxation and creep are ignored.

Example
In this example the use of the Coffin-Manson relationship will be illustrated. This is a very simple example which can be repeated at any time. The reader is encouraged to perform this test.

Product: ACME Paper Clip Model 4456
Reliability Target: 99% at a 90% confidence after 30 cycles of 45º

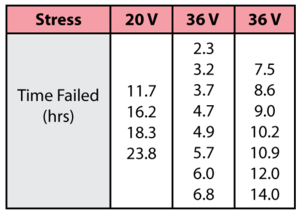
After consulting with our paper-clip engineers, the acceleration stress was determined to be the angle to which the clips are bent. Two bend stresses of 90º and 180º were used. A sample of six paper clips was tested to failure at both 90º and 180º bends with the following data obtained.

The test was performed as shown in the next figures (a side-view of the paper-clip is shown).

Using the IPL-lognormal model, determine whether the reliability target was met.


Solution
By using the IPL relationship to analyze the data, we are actually using a constant stress model to analyze a cycling process. Caution must be exercised when performing the test. The rate of change in the angle must be constant and equal for both the 90º and 180º bends and constant and equal to the rate of change in the angle for the use life of 45º bend. Rate effects are influencing the life of the paper clip. By keeping the rate constant and equal at all stress levels, we can then eliminate these rate effects from our analysis. Otherwise the analysis will not be valid.

The data were entered and analyzed using ReliaSoft's ALTA.

The parameters of the IPL-lognormal model were estimated to be:

[math]\displaystyle{ \begin{align} & \sigma = & 0.198533 \\ & K= & 0.000012 \\ & n= & 1.856808 \end{align} }[/math]

Using the QCP, the 90% lower 1-sided confidence bound on reliability after 30 cycles for a 45º bend was estimated to be [math]\displaystyle{ 99.6% }[/math] , as shown below.

This meets the target reliability of 99%.

IPL Confidence Bounds

Approximate Confidence Bounds on IPL-Exponential

Confidence Bounds on the Mean Life

From the inverse power law relationship the mean life for the exponential distribution is given by setting [math]\displaystyle{ m=L(V) }[/math] . The upper [math]\displaystyle{ ({{m}_{U}}) }[/math] and lower [math]\displaystyle{ ({{m}_{L}}) }[/math] bounds on the mean life (ML estimate of the mean life) are estimated by:

[math]\displaystyle{ {{m}_{U}}=\widehat{m}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}} }[/math]

[math]\displaystyle{ {{m}_{L}}=\widehat{m}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}} }[/math]

where [math]\displaystyle{ {{K}_{\alpha }} }[/math] is defined by:

[math]\displaystyle{ \alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }}) }[/math]

If [math]\displaystyle{ \delta }[/math] is the confidence level, then [math]\displaystyle{ \alpha =\tfrac{1-\delta }{2} }[/math] for the two-sided bounds, and [math]\displaystyle{ \alpha =1-\delta }[/math] for the one-sided bounds. The variance of [math]\displaystyle{ \widehat{m} }[/math] is given by:

[math]\displaystyle{ \begin{align} & Var(\widehat{m})= & {{\left( \frac{\partial m}{\partial K} \right)}^{2}}Var(\widehat{K})+{{\left( \frac{\partial m}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial m}{\partial K} \right)\left( \frac{\partial m}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ Var(\widehat{m})=\frac{1}{{{\widehat{K}}^{2}}{{V}^{2\widehat{n}}}}\left[ \frac{1}{{{\widehat{K}}^{2}}}Var(\widehat{K})+{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n})+\frac{2\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \right] }[/math]

The variances and covariance of [math]\displaystyle{ K }[/math] and [math]\displaystyle{ n }[/math] are estimated from the Fisher matrix (evaluated at [math]\displaystyle{ \widehat{K}, }[/math] [math]\displaystyle{ \widehat{n}) }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov(\widehat{n},\widehat{K}) & Var(\widehat{n}) \\ \end{matrix} \right]={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right]}^{-1}} }[/math]

Confidence Bounds on Reliability

The bounds on reliability at a given time, [math]\displaystyle{ T }[/math] , are estimated by:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & {{e}^{-\tfrac{T}{{{m}_{U}}}}} \\ & {{R}_{L}}= & {{e}^{-\tfrac{T}{{{m}_{L}}}}} \end{align} }[/math]

Confidence Bounds on Time

The bounds on time (ML estimate of time) for a given reliability are estimated by first solving the reliability function with respect to time:

[math]\displaystyle{ \widehat{T}=-\widehat{m}\cdot \ln (R) }[/math]

The corresponding confidence bounds are estimated from:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & -{{m}_{U}}\cdot \ln (R) \\ & {{T}_{L}}= & -{{m}_{L}}\cdot \ln (R) \end{align} }[/math]

Approximate Confidence Bounds on IPL-Weibull

Bounds on the Parameters

Using the same approach as previously discussed ( [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{K} }[/math] positive parameters):

[math]\displaystyle{ \begin{align} & {{\beta }_{U}}= & \widehat{\beta }\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}} \\ & {{\beta }_{L}}= & \widehat{\beta }\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}} \end{align} }[/math]

[math]\displaystyle{ \begin{align} & {{K}_{U}}= & \widehat{K}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} \\ & {{K}_{L}}= & \widehat{K}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} & {{n}_{U}}= & \widehat{n}+{{K}_{\alpha }}\sqrt{Var(\widehat{n})} \\ & {{n}_{L}}= & \widehat{n}-{{K}_{\alpha }}\sqrt{Var(\widehat{n})} \end{align} }[/math]

The variances and covariances of [math]\displaystyle{ \beta , }[/math] [math]\displaystyle{ K, }[/math] and [math]\displaystyle{ n }[/math] are estimated from the local Fisher matrix (evaluated at [math]\displaystyle{ \widehat{\beta }, }[/math] [math]\displaystyle{ \widehat{K}, }[/math] [math]\displaystyle{ \widehat{n}) }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var(\widehat{\beta }) & Cov(\widehat{\beta },\widehat{K}) & Cov(\widehat{\beta },\widehat{n}) \\ Cov(\widehat{K},\widehat{\beta }) & Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov(\widehat{n},\widehat{\beta }) & Cov(\widehat{n},\widehat{K}) & Var(\widehat{n}) \\ \end{matrix} \right]={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\beta }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right]}^{-1}} }[/math]

Confidence Bounds on Reliability

The reliability function (ML estimate) for the IPL-Weibull model is given by:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-{{\left( \widehat{K}{{V}^{\widehat{n}}}T \right)}^{\widehat{\beta }}}}} }[/math]

or:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-{{e}^{\ln \left[ {{\left( \widehat{K}{{V}^{\widehat{n}}}T \right)}^{\widehat{\beta }}} \right]}}}} }[/math]

Setting:

[math]\displaystyle{ \widehat{u}=\ln \left[ \left( \widehat{K}V\widehat{^{n}}T \right)\widehat{^{\beta }} \right] }[/math]

or:

[math]\displaystyle{ \widehat{u}=\widehat{\beta }\left[ \ln (T)+\ln (\widehat{K})+\widehat{n}\ln (V) \right] }[/math]

The reliability function now becomes:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-e\widehat{^{u}}}} }[/math]

The next step is to find the upper and lower bounds on [math]\displaystyle{ \widehat{u} }[/math] :

[math]\displaystyle{ {{u}_{U}}=\widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

[math]\displaystyle{ {{u}_{L}}=\widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

where:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial K} \right)}^{2}}Var(\widehat{K}) +{{\left( \frac{\partial \widehat{u}}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial K} \right)Cov(\widehat{\beta },\widehat{K})\\ & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{\beta },\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial K} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{u})= & {{\left( \frac{\widehat{u}}{\widehat{\beta }} \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\widehat{\beta }}{\widehat{K}} \right)}^{2}}Var(\widehat{K}) +{{\widehat{\beta }}^{2}}{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n}) +\frac{2\widehat{u}}{\widehat{K}}Cov(\widehat{\beta },\widehat{K})+2\widehat{u}\ln (V)Cov(\widehat{\beta },\widehat{n})+\frac{2{{\widehat{\beta }}^{2}}\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & {{e}^{-{{e}^{\left( {{u}_{L}} \right)}}}} \\ & {{R}_{L}}= & {{e}^{-{{e}^{\left( {{u}_{U}} \right)}}}} \end{align} }[/math]

Confidence Bounds on Time

The bounds on time for a given reliability (ML estimate of time) are estimated by first solving the reliability function with respect to time:

[math]\displaystyle{ \begin{align} \ln (R) &=\ -{{\left( \widehat{K}{{V}^{\widehat{n}}}\widehat{T} \right)}^{\widehat{\beta }}} \\ \ln (-\ln (R)) &=\ \widehat{\beta }\left[ \ln (\widehat{T})+\ln (\widehat{K})+\widehat{n}\ln (V) \right] \end{align} }[/math]

or:

[math]\displaystyle{ \widehat{u}=\frac{1}{\widehat{\beta }}\ln (-\ln (R))-\ln (\widehat{K})-\widehat{n}\ln (V) }[/math]

where [math]\displaystyle{ \widehat{u}=\ln \widehat{T}. }[/math] The upper and lower bounds on [math]\displaystyle{ u }[/math] are estimated from:

[math]\displaystyle{ \begin{align} & {{u}_{U}}= & \widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})} \\ & {{u}_{L}}= & \widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})} \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial K} \right)}^{2}}Var(\widehat{K}) +{{\left( \frac{\partial \widehat{u}}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial K} \right)Cov(\widehat{\beta },\widehat{K}) \\ & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{\beta },\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial K} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & \frac{1}{{{\widehat{\beta }}^{4}}}{{\left[ \ln (-\ln (R)) \right]}^{2}}Var(\widehat{\beta })+\frac{1}{{{\widehat{K}}^{2}}}Var(\widehat{K}) +{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n}) +\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}\widehat{K}}Cov(\widehat{\beta },\widehat{K}) \\ & +\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}}\ln (V)Cov(\widehat{\beta },\widehat{n}) +\frac{2\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

The upper and lower bounds on time are then found by:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & {{e}^{{{u}_{U}}}} \\ & {{T}_{L}}= & {{e}^{{{u}_{L}}}} \end{align} }[/math]

Approximate Confidence Bounds on IPL-Lognormal

Bounds on the Parameters

Since the standard deviation, [math]\displaystyle{ {{\widehat{\sigma }}_{T}} }[/math] , and [math]\displaystyle{ \widehat{K} }[/math] are positive parameters, then [math]\displaystyle{ \ln ({{\widehat{\sigma }}_{{{T}'}}}) }[/math] and [math]\displaystyle{ \ln (\widehat{K}) }[/math] are treated as normally distributed, and the bounds are estimated from:

[math]\displaystyle{ \begin{align} {{\sigma }_{U}}=\ & {{\widehat{\sigma }}_{{{T}'}}}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}} &\text{ (Upper bound)} \\ {{\sigma }_{L}}=\ & \frac{{{\widehat{\sigma }}_{{{T}'}}}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}}} &\text{ (Lower bound)} \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} {{K}_{U}}=\ & \widehat{K}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} &\text{ (Upper bound)} \\ {{K}_{L}}=\ & \frac{\widehat{K}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}}} &\text{ (Lower bound)} \end{align} }[/math]

The lower and upper bounds on [math]\displaystyle{ n }[/math] , are estimated from:

[math]\displaystyle{ \begin{align} & {{n}_{U}}= & \widehat{n}+{{K}_{\alpha }}\sqrt{Var(\widehat{n})}\text{ (Upper bound)} \\ & {{n}_{L}}= & \widehat{n}-{{K}_{\alpha }}\sqrt{Var(\widehat{n})}\text{ (Lower bound)} \end{align} }[/math]

The variances and covariances of [math]\displaystyle{ A, }[/math] [math]\displaystyle{ B, }[/math] and [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] are estimated from the local Fisher matrix (evaluated at [math]\displaystyle{ \widehat{A}, }[/math] [math]\displaystyle{ \widehat{B} }[/math] , [math]\displaystyle{ {{\widehat{\sigma }}_{{{T}'}}}), }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var({{\widehat{\sigma }}_{{{T}'}}}) & Cov(\widehat{K},{{\widehat{\sigma }}_{{{T}'}}}) & Cov(\widehat{n},{{\widehat{\sigma }}_{{{T}'}}}) \\ Cov({{\widehat{\sigma }}_{{{T}'}}},\widehat{K}) & Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov({{\widehat{\sigma }}_{{{T}'}}},\widehat{n}) & Cov(\widehat{n},\widehat{K}) & Var\left( \widehat{n} \right) \\ \end{matrix} \right]={{\left[ F \right]}^{-1}} }[/math]

where:

[math]\displaystyle{ F=\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial \sigma _{{{T}'}}^{2}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right] }[/math]

Bounds on Reliability

The reliability of the lognormal distribution is:

[math]\displaystyle{ R({T}',V;K,n,{{\sigma }_{{{T}'}}})=\int_{{{T}'}}^{\infty }\frac{1}{{{\widehat{\sigma }}_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}} \right)}^{2}}}}dt }[/math]

Let [math]\displaystyle{ \widehat{z}(t,V;K,n,{{\sigma }_{T}})=\tfrac{t+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}}, }[/math] then [math]\displaystyle{ \tfrac{d\widehat{z}}{dt}=\tfrac{1}{{{\widehat{\sigma }}_{{{T}'}}}}. }[/math]

For [math]\displaystyle{ t={T}' }[/math] , [math]\displaystyle{ \widehat{z}=\tfrac{{T}'+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}} }[/math] , and for [math]\displaystyle{ t=\infty , }[/math] [math]\displaystyle{ \widehat{z}=\infty . }[/math] The above equation then becomes:

[math]\displaystyle{ R(\widehat{z})=\int_{\widehat{z}({T}',V)}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz }[/math]

The bounds on [math]\displaystyle{ z }[/math] are estimated from:

[math]\displaystyle{ \begin{align} & {{z}_{U}}= & \widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \\ & {{z}_{L}}= & \widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \end{align} }[/math]

where:

.

[math]\displaystyle{ \begin{align} Var(\widehat{z})= & \left( \frac{\partial \widehat{z}}{\partial K} \right)_{\widehat{K}}^{2}Var(\widehat{K})+\left( \frac{\partial \widehat{z}}{\partial n} \right)_{\widehat{n}}^{2}Var(\widehat{n})+\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)_{{{\widehat{\sigma }}_{{{T}'}}}}^{2}Var({{\widehat{\sigma }}_{T}}) +2{{\left( \frac{\partial \widehat{z}}{\partial K} \right)}_{\widehat{K}}}{{\left( \frac{\partial \widehat{z}}{\partial n} \right)}_{\widehat{n}}}Cov\left( \widehat{K},\widehat{n} \right) \\ & +2{{\left( \frac{\partial \widehat{z}}{\partial K} \right)}_{\widehat{K}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{K},{{\widehat{\sigma }}_{T}} \right) +2{{\left( \frac{\partial \widehat{z}}{\partial n} \right)}_{\widehat{n}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{n},{{\widehat{\sigma }}_{T}} \right) \end{align} }[/math].

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{z})= & \frac{1}{\widehat{\sigma }_{{{T}'}}^{2}}[\frac{1}{{{K}^{2}}}Var(\widehat{K})+\ln {{(V)}^{2}}Var(\widehat{n})+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +\frac{2\ln (V)}{K}Cov\left( \widehat{K},\widehat{n} \right)-\frac{2\widehat{z}}{K}Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right)-2\widehat{z}\ln (V)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right)] \end{align} }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & \int_{{{z}_{L}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Upper bound)} \\ & {{R}_{L}}= & \int_{{{z}_{U}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Lower bound)} \end{align} }[/math]

Confidence Bounds on Time

The bounds around time, for a given lognormal percentile (unreliability), are estimated by first solving the reliability equation with respect to time, as follows:

[math]\displaystyle{ {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}})=-\ln (\widehat{K})-\widehat{n}\ln (V)+z\cdot {{\widehat{\sigma }}_{{{T}'}}} }[/math]

where:

[math]\displaystyle{ \begin{align} & {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}})=\ \ln (T) \\ \\ & z=\ {{\Phi }^{-1}}\left[ F({T}') \right] \end{align} }[/math]

and:

[math]\displaystyle{ \Phi (z)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{z({T}')}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz }[/math]

The next step is to calculate the variance of [math]\displaystyle{ {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}}): }[/math]

[math]\displaystyle{ \begin{align} Var({T}')= & {{\left( \frac{\partial {T}'}{\partial K} \right)}^{2}}Var(\widehat{K})+{{\left( \frac{\partial {T}'}{\partial n} \right)}^{2}}Var(\widehat{n})+{{\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +2\left( \frac{\partial {T}'}{\partial K} \right)\left( \frac{\partial {T}'}{\partial n} \right)Cov\left( \widehat{K},\widehat{n} \right) \\ & +2\left( \frac{\partial {T}'}{\partial K} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right) +2\left( \frac{\partial {T}'}{\partial n} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} Var({T}')= & \frac{1}{{{K}^{2}}}Var(\widehat{K})+\ln {{(V)}^{2}}Var(\widehat{n})+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +\frac{2\ln (V)}{K}Cov\left( \widehat{K},\widehat{n} \right) \\ & -\frac{2\widehat{z}}{K}Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right) -2\widehat{z}\ln (V)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) \end{align} }[/math]

The upper and lower bounds are then found by:

[math]\displaystyle{ \begin{align} & T_{U}^{\prime }= & \ln {{T}_{U}}={T}'+{{K}_{\alpha }}\sqrt{Var({T}')} \\ & T_{L}^{\prime }= & \ln {{T}_{L}}={T}'-{{K}_{\alpha }}\sqrt{Var({T}')} \end{align} }[/math]

Solving for [math]\displaystyle{ {{T}_{U}} }[/math] and [math]\displaystyle{ {{T}_{L}} }[/math] yields:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & {{e}^{T_{U}^{\prime }}}\text{ (Upper bound)} \\ & {{T}_{L}}= & {{e}^{T_{L}^{\prime }}}\text{ (Lower bound)} \end{align} }[/math]

Consider the following times-to-failure data at two different stress levels.

The data set was analyzed jointly in an ALTA standard folio using the IPL-Weibull model, with a complete MLE solution over the entire data set. The analysis yields:

[math]\displaystyle{ \widehat{\beta }=2.616464\,\! }[/math]

[math]\displaystyle{ \widehat{K}=0.001022\,\! }[/math]

[math]\displaystyle{ \widehat{n}=1.327292\,\! }[/math]

Introduction

The inverse power law (IPL) model (or relationship) is commonly used for non-thermal accelerated stresses and is given by:

[math]\displaystyle{ L(V)=\frac{1}{K{{V}^{n}}} }[/math]

where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, [math]\displaystyle{ B(x) }[/math] life, etc.

• [math]\displaystyle{ V }[/math] represents the stress level.

• [math]\displaystyle{ K }[/math] is one of the model parameters to be determined, [math]\displaystyle{ (K\gt 0). }[/math]

• [math]\displaystyle{ n }[/math] is another model parameter to be determined.

The inverse power law appears as a straight line when plotted on a log-log paper. The equation of the line is given by:

[math]\displaystyle{ \ln (L)=-\ln (K)-n\ln (V) }[/math]

Plotting methods are widely used in estimating the parameters of the inverse power law relationship since obtaining [math]\displaystyle{ K }[/math] and [math]\displaystyle{ n }[/math] is as simple as finding the slope and the intercept in the above equation.

A Look at the Parameter [math]\displaystyle{ n }[/math]

The parameter [math]\displaystyle{ n }[/math] in the inverse power relationship is a measure of the effect of the stress on the life. As the absolute value of [math]\displaystyle{ n }[/math] increases, the greater the effect of the stress. Negative values of [math]\displaystyle{ n }[/math] indicate an increasing life with increasing stress. An absolute value of [math]\displaystyle{ n }[/math] approaching zero indicates small effect of the stress on the life, with no effect (constant life with stress) when [math]\displaystyle{ n=0. }[/math]

Acceleration Factor=

For the IPL relationship the acceleration factor is given by:

[math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{\tfrac{1}{KV_{u}^{n}}}{\tfrac{1}{KV_{A}^{n}}}={{\left( \frac{{{V}_{A}}}{{{V}_{u}}} \right)}^{n}} }[/math]

where:
• [math]\displaystyle{ {{L}_{USE}} }[/math] is the life at use stress level.

• [math]\displaystyle{ {{L}_{Accelerated}} }[/math] is the life at the accelerated stress level.

• [math]\displaystyle{ {{V}_{u}} }[/math] is the use stress level.

• [math]\displaystyle{ {{V}_{A}} }[/math] is the accelerated stress level.

Consider the following times-to-failure data at two different stress levels.

The data set was analyzed jointly in an ALTA standard folio using the IPL-Weibull model, with a complete MLE solution over the entire data set. The analysis yields:

[math]\displaystyle{ \widehat{\beta }=2.616464\,\! }[/math]

[math]\displaystyle{ \widehat{K}=0.001022\,\! }[/math]

[math]\displaystyle{ \widehat{n}=1.327292\,\! }[/math]

IPL and the Coffin-Manson Relationship

In accelerated life testing analysis, thermal cycling is commonly treated as a low-cycle fatigue problem, using the inverse power law relationship. Coffin and Manson suggested that the number of cycles-to-failure of a metal subjected to thermal cycling is given by [28]:

[math]\displaystyle{ N=\frac{C}{{{\left( \Delta T \right)}^{\gamma }}} }[/math]

where:
• [math]\displaystyle{ N }[/math] is the number of cycles to failure.
• [math]\displaystyle{ C }[/math] is a constant, characteristic of the metal.
• [math]\displaystyle{ \gamma }[/math] is another constant, also characteristic of the metal.
• [math]\displaystyle{ \Delta T }[/math] is the range of the thermal cycle.

This relationship is basically the inverse power law relationship, where the stress [math]\displaystyle{ V, }[/math] is substituted by the range [math]\displaystyle{ \Delta V }[/math]. This is an attempt to simplify the analysis of a time-varying stress test by using a constant stress model. It is a very commonly used methodology for thermal cycling and mechanical fatigue tests. However, by performing such a simplification, the following assumptions and shortcomings are inevitable. First, the acceleration effects due to the stress rate of change are ignored. In other words, it is assumed that the failures are accelerated by the stress difference and not by how rapidly this difference occurs. Secondly, the acceleration effects due to stress relaxation and creep are ignored.

Example
In this example the use of the Coffin-Manson relationship will be illustrated. This is a very simple example which can be repeated at any time. The reader is encouraged to perform this test.

Product: ACME Paper Clip Model 4456
Reliability Target: 99% at a 90% confidence after 30 cycles of 45º

After consulting with our paper-clip engineers, the acceleration stress was determined to be the angle to which the clips are bent. Two bend stresses of 90º and 180º were used. A sample of six paper clips was tested to failure at both 90º and 180º bends with the following data obtained.

The test was performed as shown in the next figures (a side-view of the paper-clip is shown).

Using the IPL-lognormal model, determine whether the reliability target was met.


Solution
By using the IPL relationship to analyze the data, we are actually using a constant stress model to analyze a cycling process. Caution must be exercised when performing the test. The rate of change in the angle must be constant and equal for both the 90º and 180º bends and constant and equal to the rate of change in the angle for the use life of 45º bend. Rate effects are influencing the life of the paper clip. By keeping the rate constant and equal at all stress levels, we can then eliminate these rate effects from our analysis. Otherwise the analysis will not be valid.

The data were entered and analyzed using ReliaSoft's ALTA.

The parameters of the IPL-lognormal model were estimated to be:

[math]\displaystyle{ \begin{align} & \sigma = & 0.198533 \\ & K= & 0.000012 \\ & n= & 1.856808 \end{align} }[/math]

Using the QCP, the 90% lower 1-sided confidence bound on reliability after 30 cycles for a 45º bend was estimated to be [math]\displaystyle{ 99.6% }[/math] , as shown below.

This meets the target reliability of 99%.

IPL Confidence Bounds

Approximate Confidence Bounds on IPL-Exponential

Confidence Bounds on the Mean Life

From the inverse power law relationship the mean life for the exponential distribution is given by setting [math]\displaystyle{ m=L(V) }[/math] . The upper [math]\displaystyle{ ({{m}_{U}}) }[/math] and lower [math]\displaystyle{ ({{m}_{L}}) }[/math] bounds on the mean life (ML estimate of the mean life) are estimated by:

[math]\displaystyle{ {{m}_{U}}=\widehat{m}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}} }[/math]

[math]\displaystyle{ {{m}_{L}}=\widehat{m}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}} }[/math]

where [math]\displaystyle{ {{K}_{\alpha }} }[/math] is defined by:

[math]\displaystyle{ \alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }}) }[/math]

If [math]\displaystyle{ \delta }[/math] is the confidence level, then [math]\displaystyle{ \alpha =\tfrac{1-\delta }{2} }[/math] for the two-sided bounds, and [math]\displaystyle{ \alpha =1-\delta }[/math] for the one-sided bounds. The variance of [math]\displaystyle{ \widehat{m} }[/math] is given by:

[math]\displaystyle{ \begin{align} & Var(\widehat{m})= & {{\left( \frac{\partial m}{\partial K} \right)}^{2}}Var(\widehat{K})+{{\left( \frac{\partial m}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial m}{\partial K} \right)\left( \frac{\partial m}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ Var(\widehat{m})=\frac{1}{{{\widehat{K}}^{2}}{{V}^{2\widehat{n}}}}\left[ \frac{1}{{{\widehat{K}}^{2}}}Var(\widehat{K})+{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n})+\frac{2\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \right] }[/math]

The variances and covariance of [math]\displaystyle{ K }[/math] and [math]\displaystyle{ n }[/math] are estimated from the Fisher matrix (evaluated at [math]\displaystyle{ \widehat{K}, }[/math] [math]\displaystyle{ \widehat{n}) }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov(\widehat{n},\widehat{K}) & Var(\widehat{n}) \\ \end{matrix} \right]={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right]}^{-1}} }[/math]

Confidence Bounds on Reliability

The bounds on reliability at a given time, [math]\displaystyle{ T }[/math] , are estimated by:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & {{e}^{-\tfrac{T}{{{m}_{U}}}}} \\ & {{R}_{L}}= & {{e}^{-\tfrac{T}{{{m}_{L}}}}} \end{align} }[/math]

Confidence Bounds on Time

The bounds on time (ML estimate of time) for a given reliability are estimated by first solving the reliability function with respect to time:

[math]\displaystyle{ \widehat{T}=-\widehat{m}\cdot \ln (R) }[/math]

The corresponding confidence bounds are estimated from:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & -{{m}_{U}}\cdot \ln (R) \\ & {{T}_{L}}= & -{{m}_{L}}\cdot \ln (R) \end{align} }[/math]

Approximate Confidence Bounds on IPL-Weibull

Bounds on the Parameters

Using the same approach as previously discussed ( [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{K} }[/math] positive parameters):

[math]\displaystyle{ \begin{align} & {{\beta }_{U}}= & \widehat{\beta }\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}} \\ & {{\beta }_{L}}= & \widehat{\beta }\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}} \end{align} }[/math]

[math]\displaystyle{ \begin{align} & {{K}_{U}}= & \widehat{K}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} \\ & {{K}_{L}}= & \widehat{K}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} & {{n}_{U}}= & \widehat{n}+{{K}_{\alpha }}\sqrt{Var(\widehat{n})} \\ & {{n}_{L}}= & \widehat{n}-{{K}_{\alpha }}\sqrt{Var(\widehat{n})} \end{align} }[/math]

The variances and covariances of [math]\displaystyle{ \beta , }[/math] [math]\displaystyle{ K, }[/math] and [math]\displaystyle{ n }[/math] are estimated from the local Fisher matrix (evaluated at [math]\displaystyle{ \widehat{\beta }, }[/math] [math]\displaystyle{ \widehat{K}, }[/math] [math]\displaystyle{ \widehat{n}) }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var(\widehat{\beta }) & Cov(\widehat{\beta },\widehat{K}) & Cov(\widehat{\beta },\widehat{n}) \\ Cov(\widehat{K},\widehat{\beta }) & Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov(\widehat{n},\widehat{\beta }) & Cov(\widehat{n},\widehat{K}) & Var(\widehat{n}) \\ \end{matrix} \right]={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\beta }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right]}^{-1}} }[/math]

Confidence Bounds on Reliability

The reliability function (ML estimate) for the IPL-Weibull model is given by:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-{{\left( \widehat{K}{{V}^{\widehat{n}}}T \right)}^{\widehat{\beta }}}}} }[/math]

or:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-{{e}^{\ln \left[ {{\left( \widehat{K}{{V}^{\widehat{n}}}T \right)}^{\widehat{\beta }}} \right]}}}} }[/math]

Setting:

[math]\displaystyle{ \widehat{u}=\ln \left[ \left( \widehat{K}V\widehat{^{n}}T \right)\widehat{^{\beta }} \right] }[/math]

or:

[math]\displaystyle{ \widehat{u}=\widehat{\beta }\left[ \ln (T)+\ln (\widehat{K})+\widehat{n}\ln (V) \right] }[/math]

The reliability function now becomes:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-e\widehat{^{u}}}} }[/math]

The next step is to find the upper and lower bounds on [math]\displaystyle{ \widehat{u} }[/math] :

[math]\displaystyle{ {{u}_{U}}=\widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

[math]\displaystyle{ {{u}_{L}}=\widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

where:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial K} \right)}^{2}}Var(\widehat{K}) +{{\left( \frac{\partial \widehat{u}}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial K} \right)Cov(\widehat{\beta },\widehat{K})\\ & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{\beta },\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial K} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{u})= & {{\left( \frac{\widehat{u}}{\widehat{\beta }} \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\widehat{\beta }}{\widehat{K}} \right)}^{2}}Var(\widehat{K}) +{{\widehat{\beta }}^{2}}{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n}) +\frac{2\widehat{u}}{\widehat{K}}Cov(\widehat{\beta },\widehat{K})+2\widehat{u}\ln (V)Cov(\widehat{\beta },\widehat{n})+\frac{2{{\widehat{\beta }}^{2}}\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & {{e}^{-{{e}^{\left( {{u}_{L}} \right)}}}} \\ & {{R}_{L}}= & {{e}^{-{{e}^{\left( {{u}_{U}} \right)}}}} \end{align} }[/math]

Confidence Bounds on Time

The bounds on time for a given reliability (ML estimate of time) are estimated by first solving the reliability function with respect to time:

[math]\displaystyle{ \begin{align} \ln (R) &=\ -{{\left( \widehat{K}{{V}^{\widehat{n}}}\widehat{T} \right)}^{\widehat{\beta }}} \\ \ln (-\ln (R)) &=\ \widehat{\beta }\left[ \ln (\widehat{T})+\ln (\widehat{K})+\widehat{n}\ln (V) \right] \end{align} }[/math]

or:

[math]\displaystyle{ \widehat{u}=\frac{1}{\widehat{\beta }}\ln (-\ln (R))-\ln (\widehat{K})-\widehat{n}\ln (V) }[/math]

where [math]\displaystyle{ \widehat{u}=\ln \widehat{T}. }[/math] The upper and lower bounds on [math]\displaystyle{ u }[/math] are estimated from:

[math]\displaystyle{ \begin{align} & {{u}_{U}}= & \widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})} \\ & {{u}_{L}}= & \widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})} \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial K} \right)}^{2}}Var(\widehat{K}) +{{\left( \frac{\partial \widehat{u}}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial K} \right)Cov(\widehat{\beta },\widehat{K}) \\ & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{\beta },\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial K} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & \frac{1}{{{\widehat{\beta }}^{4}}}{{\left[ \ln (-\ln (R)) \right]}^{2}}Var(\widehat{\beta })+\frac{1}{{{\widehat{K}}^{2}}}Var(\widehat{K}) +{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n}) +\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}\widehat{K}}Cov(\widehat{\beta },\widehat{K}) \\ & +\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}}\ln (V)Cov(\widehat{\beta },\widehat{n}) +\frac{2\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

The upper and lower bounds on time are then found by:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & {{e}^{{{u}_{U}}}} \\ & {{T}_{L}}= & {{e}^{{{u}_{L}}}} \end{align} }[/math]

Approximate Confidence Bounds on IPL-Lognormal

Bounds on the Parameters

Since the standard deviation, [math]\displaystyle{ {{\widehat{\sigma }}_{T}} }[/math] , and [math]\displaystyle{ \widehat{K} }[/math] are positive parameters, then [math]\displaystyle{ \ln ({{\widehat{\sigma }}_{{{T}'}}}) }[/math] and [math]\displaystyle{ \ln (\widehat{K}) }[/math] are treated as normally distributed, and the bounds are estimated from:

[math]\displaystyle{ \begin{align} {{\sigma }_{U}}=\ & {{\widehat{\sigma }}_{{{T}'}}}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}} &\text{ (Upper bound)} \\ {{\sigma }_{L}}=\ & \frac{{{\widehat{\sigma }}_{{{T}'}}}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}}} &\text{ (Lower bound)} \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} {{K}_{U}}=\ & \widehat{K}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} &\text{ (Upper bound)} \\ {{K}_{L}}=\ & \frac{\widehat{K}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}}} &\text{ (Lower bound)} \end{align} }[/math]

The lower and upper bounds on [math]\displaystyle{ n }[/math] , are estimated from:

[math]\displaystyle{ \begin{align} & {{n}_{U}}= & \widehat{n}+{{K}_{\alpha }}\sqrt{Var(\widehat{n})}\text{ (Upper bound)} \\ & {{n}_{L}}= & \widehat{n}-{{K}_{\alpha }}\sqrt{Var(\widehat{n})}\text{ (Lower bound)} \end{align} }[/math]

The variances and covariances of [math]\displaystyle{ A, }[/math] [math]\displaystyle{ B, }[/math] and [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] are estimated from the local Fisher matrix (evaluated at [math]\displaystyle{ \widehat{A}, }[/math] [math]\displaystyle{ \widehat{B} }[/math] , [math]\displaystyle{ {{\widehat{\sigma }}_{{{T}'}}}), }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var({{\widehat{\sigma }}_{{{T}'}}}) & Cov(\widehat{K},{{\widehat{\sigma }}_{{{T}'}}}) & Cov(\widehat{n},{{\widehat{\sigma }}_{{{T}'}}}) \\ Cov({{\widehat{\sigma }}_{{{T}'}}},\widehat{K}) & Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov({{\widehat{\sigma }}_{{{T}'}}},\widehat{n}) & Cov(\widehat{n},\widehat{K}) & Var\left( \widehat{n} \right) \\ \end{matrix} \right]={{\left[ F \right]}^{-1}} }[/math]

where:

[math]\displaystyle{ F=\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial \sigma _{{{T}'}}^{2}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right] }[/math]

Bounds on Reliability

The reliability of the lognormal distribution is:

[math]\displaystyle{ R({T}',V;K,n,{{\sigma }_{{{T}'}}})=\int_{{{T}'}}^{\infty }\frac{1}{{{\widehat{\sigma }}_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}} \right)}^{2}}}}dt }[/math]

Let [math]\displaystyle{ \widehat{z}(t,V;K,n,{{\sigma }_{T}})=\tfrac{t+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}}, }[/math] then [math]\displaystyle{ \tfrac{d\widehat{z}}{dt}=\tfrac{1}{{{\widehat{\sigma }}_{{{T}'}}}}. }[/math]

For [math]\displaystyle{ t={T}' }[/math] , [math]\displaystyle{ \widehat{z}=\tfrac{{T}'+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}} }[/math] , and for [math]\displaystyle{ t=\infty , }[/math] [math]\displaystyle{ \widehat{z}=\infty . }[/math] The above equation then becomes:

[math]\displaystyle{ R(\widehat{z})=\int_{\widehat{z}({T}',V)}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz }[/math]

The bounds on [math]\displaystyle{ z }[/math] are estimated from:

[math]\displaystyle{ \begin{align} & {{z}_{U}}= & \widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \\ & {{z}_{L}}= & \widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \end{align} }[/math]

where:

.

[math]\displaystyle{ \begin{align} Var(\widehat{z})= & \left( \frac{\partial \widehat{z}}{\partial K} \right)_{\widehat{K}}^{2}Var(\widehat{K})+\left( \frac{\partial \widehat{z}}{\partial n} \right)_{\widehat{n}}^{2}Var(\widehat{n})+\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)_{{{\widehat{\sigma }}_{{{T}'}}}}^{2}Var({{\widehat{\sigma }}_{T}}) +2{{\left( \frac{\partial \widehat{z}}{\partial K} \right)}_{\widehat{K}}}{{\left( \frac{\partial \widehat{z}}{\partial n} \right)}_{\widehat{n}}}Cov\left( \widehat{K},\widehat{n} \right) \\ & +2{{\left( \frac{\partial \widehat{z}}{\partial K} \right)}_{\widehat{K}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{K},{{\widehat{\sigma }}_{T}} \right) +2{{\left( \frac{\partial \widehat{z}}{\partial n} \right)}_{\widehat{n}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{n},{{\widehat{\sigma }}_{T}} \right) \end{align} }[/math].

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{z})= & \frac{1}{\widehat{\sigma }_{{{T}'}}^{2}}[\frac{1}{{{K}^{2}}}Var(\widehat{K})+\ln {{(V)}^{2}}Var(\widehat{n})+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +\frac{2\ln (V)}{K}Cov\left( \widehat{K},\widehat{n} \right)-\frac{2\widehat{z}}{K}Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right)-2\widehat{z}\ln (V)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right)] \end{align} }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & \int_{{{z}_{L}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Upper bound)} \\ & {{R}_{L}}= & \int_{{{z}_{U}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Lower bound)} \end{align} }[/math]

Confidence Bounds on Time

The bounds around time, for a given lognormal percentile (unreliability), are estimated by first solving the reliability equation with respect to time, as follows:

[math]\displaystyle{ {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}})=-\ln (\widehat{K})-\widehat{n}\ln (V)+z\cdot {{\widehat{\sigma }}_{{{T}'}}} }[/math]

where:

[math]\displaystyle{ \begin{align} & {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}})=\ \ln (T) \\ \\ & z=\ {{\Phi }^{-1}}\left[ F({T}') \right] \end{align} }[/math]

and:

[math]\displaystyle{ \Phi (z)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{z({T}')}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz }[/math]

The next step is to calculate the variance of [math]\displaystyle{ {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}}): }[/math]

[math]\displaystyle{ \begin{align} Var({T}')= & {{\left( \frac{\partial {T}'}{\partial K} \right)}^{2}}Var(\widehat{K})+{{\left( \frac{\partial {T}'}{\partial n} \right)}^{2}}Var(\widehat{n})+{{\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +2\left( \frac{\partial {T}'}{\partial K} \right)\left( \frac{\partial {T}'}{\partial n} \right)Cov\left( \widehat{K},\widehat{n} \right) \\ & +2\left( \frac{\partial {T}'}{\partial K} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right) +2\left( \frac{\partial {T}'}{\partial n} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} Var({T}')= & \frac{1}{{{K}^{2}}}Var(\widehat{K})+\ln {{(V)}^{2}}Var(\widehat{n})+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +\frac{2\ln (V)}{K}Cov\left( \widehat{K},\widehat{n} \right) \\ & -\frac{2\widehat{z}}{K}Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right) -2\widehat{z}\ln (V)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) \end{align} }[/math]

The upper and lower bounds are then found by:

[math]\displaystyle{ \begin{align} & T_{U}^{\prime }= & \ln {{T}_{U}}={T}'+{{K}_{\alpha }}\sqrt{Var({T}')} \\ & T_{L}^{\prime }= & \ln {{T}_{L}}={T}'-{{K}_{\alpha }}\sqrt{Var({T}')} \end{align} }[/math]

Solving for [math]\displaystyle{ {{T}_{U}} }[/math] and [math]\displaystyle{ {{T}_{L}} }[/math] yields:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & {{e}^{T_{U}^{\prime }}}\text{ (Upper bound)} \\ & {{T}_{L}}= & {{e}^{T_{L}^{\prime }}}\text{ (Lower bound)} \end{align} }[/math]

IPL and the Coffin-Manson Relationship

In accelerated life testing analysis, thermal cycling is commonly treated as a low-cycle fatigue problem, using the inverse power law relationship. Coffin and Manson suggested that the number of cycles-to-failure of a metal subjected to thermal cycling is given by [28]:

[math]\displaystyle{ N=\frac{C}{{{\left( \Delta T \right)}^{\gamma }}} }[/math]

where:
• [math]\displaystyle{ N }[/math] is the number of cycles to failure.
• [math]\displaystyle{ C }[/math] is a constant, characteristic of the metal.
• [math]\displaystyle{ \gamma }[/math] is another constant, also characteristic of the metal.
• [math]\displaystyle{ \Delta T }[/math] is the range of the thermal cycle.

This relationship is basically the inverse power law relationship, where the stress [math]\displaystyle{ V, }[/math] is substituted by the range [math]\displaystyle{ \Delta V }[/math]. This is an attempt to simplify the analysis of a time-varying stress test by using a constant stress model. It is a very commonly used methodology for thermal cycling and mechanical fatigue tests. However, by performing such a simplification, the following assumptions and shortcomings are inevitable. First, the acceleration effects due to the stress rate of change are ignored. In other words, it is assumed that the failures are accelerated by the stress difference and not by how rapidly this difference occurs. Secondly, the acceleration effects due to stress relaxation and creep are ignored.

Example
In this example the use of the Coffin-Manson relationship will be illustrated. This is a very simple example which can be repeated at any time. The reader is encouraged to perform this test.

Product: ACME Paper Clip Model 4456
Reliability Target: 99% at a 90% confidence after 30 cycles of 45º

After consulting with our paper-clip engineers, the acceleration stress was determined to be the angle to which the clips are bent. Two bend stresses of 90º and 180º were used. A sample of six paper clips was tested to failure at both 90º and 180º bends with the following data obtained.

The test was performed as shown in the next figures (a side-view of the paper-clip is shown).

Using the IPL-lognormal model, determine whether the reliability target was met.


Solution
By using the IPL relationship to analyze the data, we are actually using a constant stress model to analyze a cycling process. Caution must be exercised when performing the test. The rate of change in the angle must be constant and equal for both the 90º and 180º bends and constant and equal to the rate of change in the angle for the use life of 45º bend. Rate effects are influencing the life of the paper clip. By keeping the rate constant and equal at all stress levels, we can then eliminate these rate effects from our analysis. Otherwise the analysis will not be valid.

The data were entered and analyzed using ReliaSoft's ALTA.

The parameters of the IPL-lognormal model were estimated to be:

[math]\displaystyle{ \begin{align} & \sigma = & 0.198533 \\ & K= & 0.000012 \\ & n= & 1.856808 \end{align} }[/math]

Using the QCP, the 90% lower 1-sided confidence bound on reliability after 30 cycles for a 45º bend was estimated to be [math]\displaystyle{ 99.6% }[/math] , as shown below.

This meets the target reliability of 99%.

IPL Confidence Bounds

Approximate Confidence Bounds on IPL-Exponential

Confidence Bounds on the Mean Life

From the inverse power law relationship the mean life for the exponential distribution is given by setting [math]\displaystyle{ m=L(V) }[/math] . The upper [math]\displaystyle{ ({{m}_{U}}) }[/math] and lower [math]\displaystyle{ ({{m}_{L}}) }[/math] bounds on the mean life (ML estimate of the mean life) are estimated by:

[math]\displaystyle{ {{m}_{U}}=\widehat{m}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}} }[/math]

[math]\displaystyle{ {{m}_{L}}=\widehat{m}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{m})}}{\widehat{m}}}} }[/math]

where [math]\displaystyle{ {{K}_{\alpha }} }[/math] is defined by:

[math]\displaystyle{ \alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }}) }[/math]

If [math]\displaystyle{ \delta }[/math] is the confidence level, then [math]\displaystyle{ \alpha =\tfrac{1-\delta }{2} }[/math] for the two-sided bounds, and [math]\displaystyle{ \alpha =1-\delta }[/math] for the one-sided bounds. The variance of [math]\displaystyle{ \widehat{m} }[/math] is given by:

[math]\displaystyle{ \begin{align} & Var(\widehat{m})= & {{\left( \frac{\partial m}{\partial K} \right)}^{2}}Var(\widehat{K})+{{\left( \frac{\partial m}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial m}{\partial K} \right)\left( \frac{\partial m}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ Var(\widehat{m})=\frac{1}{{{\widehat{K}}^{2}}{{V}^{2\widehat{n}}}}\left[ \frac{1}{{{\widehat{K}}^{2}}}Var(\widehat{K})+{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n})+\frac{2\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \right] }[/math]

The variances and covariance of [math]\displaystyle{ K }[/math] and [math]\displaystyle{ n }[/math] are estimated from the Fisher matrix (evaluated at [math]\displaystyle{ \widehat{K}, }[/math] [math]\displaystyle{ \widehat{n}) }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov(\widehat{n},\widehat{K}) & Var(\widehat{n}) \\ \end{matrix} \right]={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right]}^{-1}} }[/math]

Confidence Bounds on Reliability

The bounds on reliability at a given time, [math]\displaystyle{ T }[/math] , are estimated by:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & {{e}^{-\tfrac{T}{{{m}_{U}}}}} \\ & {{R}_{L}}= & {{e}^{-\tfrac{T}{{{m}_{L}}}}} \end{align} }[/math]

Confidence Bounds on Time

The bounds on time (ML estimate of time) for a given reliability are estimated by first solving the reliability function with respect to time:

[math]\displaystyle{ \widehat{T}=-\widehat{m}\cdot \ln (R) }[/math]

The corresponding confidence bounds are estimated from:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & -{{m}_{U}}\cdot \ln (R) \\ & {{T}_{L}}= & -{{m}_{L}}\cdot \ln (R) \end{align} }[/math]

Approximate Confidence Bounds on IPL-Weibull

Bounds on the Parameters

Using the same approach as previously discussed ( [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{K} }[/math] positive parameters):

[math]\displaystyle{ \begin{align} & {{\beta }_{U}}= & \widehat{\beta }\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}} \\ & {{\beta }_{L}}= & \widehat{\beta }\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{\beta })}}{\widehat{\beta }}}} \end{align} }[/math]

[math]\displaystyle{ \begin{align} & {{K}_{U}}= & \widehat{K}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} \\ & {{K}_{L}}= & \widehat{K}\cdot {{e}^{-\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} & {{n}_{U}}= & \widehat{n}+{{K}_{\alpha }}\sqrt{Var(\widehat{n})} \\ & {{n}_{L}}= & \widehat{n}-{{K}_{\alpha }}\sqrt{Var(\widehat{n})} \end{align} }[/math]

The variances and covariances of [math]\displaystyle{ \beta , }[/math] [math]\displaystyle{ K, }[/math] and [math]\displaystyle{ n }[/math] are estimated from the local Fisher matrix (evaluated at [math]\displaystyle{ \widehat{\beta }, }[/math] [math]\displaystyle{ \widehat{K}, }[/math] [math]\displaystyle{ \widehat{n}) }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var(\widehat{\beta }) & Cov(\widehat{\beta },\widehat{K}) & Cov(\widehat{\beta },\widehat{n}) \\ Cov(\widehat{K},\widehat{\beta }) & Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov(\widehat{n},\widehat{\beta }) & Cov(\widehat{n},\widehat{K}) & Var(\widehat{n}) \\ \end{matrix} \right]={{\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\beta }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \beta \partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial \beta } & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial A} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right]}^{-1}} }[/math]

Confidence Bounds on Reliability

The reliability function (ML estimate) for the IPL-Weibull model is given by:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-{{\left( \widehat{K}{{V}^{\widehat{n}}}T \right)}^{\widehat{\beta }}}}} }[/math]

or:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-{{e}^{\ln \left[ {{\left( \widehat{K}{{V}^{\widehat{n}}}T \right)}^{\widehat{\beta }}} \right]}}}} }[/math]

Setting:

[math]\displaystyle{ \widehat{u}=\ln \left[ \left( \widehat{K}V\widehat{^{n}}T \right)\widehat{^{\beta }} \right] }[/math]

or:

[math]\displaystyle{ \widehat{u}=\widehat{\beta }\left[ \ln (T)+\ln (\widehat{K})+\widehat{n}\ln (V) \right] }[/math]

The reliability function now becomes:

[math]\displaystyle{ \widehat{R}(T,V)={{e}^{-e\widehat{^{u}}}} }[/math]

The next step is to find the upper and lower bounds on [math]\displaystyle{ \widehat{u} }[/math] :

[math]\displaystyle{ {{u}_{U}}=\widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

[math]\displaystyle{ {{u}_{L}}=\widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})} }[/math]

where:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial K} \right)}^{2}}Var(\widehat{K}) +{{\left( \frac{\partial \widehat{u}}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial K} \right)Cov(\widehat{\beta },\widehat{K})\\ & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{\beta },\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial K} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{u})= & {{\left( \frac{\widehat{u}}{\widehat{\beta }} \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\widehat{\beta }}{\widehat{K}} \right)}^{2}}Var(\widehat{K}) +{{\widehat{\beta }}^{2}}{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n}) +\frac{2\widehat{u}}{\widehat{K}}Cov(\widehat{\beta },\widehat{K})+2\widehat{u}\ln (V)Cov(\widehat{\beta },\widehat{n})+\frac{2{{\widehat{\beta }}^{2}}\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & {{e}^{-{{e}^{\left( {{u}_{L}} \right)}}}} \\ & {{R}_{L}}= & {{e}^{-{{e}^{\left( {{u}_{U}} \right)}}}} \end{align} }[/math]

Confidence Bounds on Time

The bounds on time for a given reliability (ML estimate of time) are estimated by first solving the reliability function with respect to time:

[math]\displaystyle{ \begin{align} \ln (R) &=\ -{{\left( \widehat{K}{{V}^{\widehat{n}}}\widehat{T} \right)}^{\widehat{\beta }}} \\ \ln (-\ln (R)) &=\ \widehat{\beta }\left[ \ln (\widehat{T})+\ln (\widehat{K})+\widehat{n}\ln (V) \right] \end{align} }[/math]

or:

[math]\displaystyle{ \widehat{u}=\frac{1}{\widehat{\beta }}\ln (-\ln (R))-\ln (\widehat{K})-\widehat{n}\ln (V) }[/math]

where [math]\displaystyle{ \widehat{u}=\ln \widehat{T}. }[/math] The upper and lower bounds on [math]\displaystyle{ u }[/math] are estimated from:

[math]\displaystyle{ \begin{align} & {{u}_{U}}= & \widehat{u}+{{K}_{\alpha }}\sqrt{Var(\widehat{u})} \\ & {{u}_{L}}= & \widehat{u}-{{K}_{\alpha }}\sqrt{Var(\widehat{u})} \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & {{\left( \frac{\partial \widehat{u}}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial \widehat{u}}{\partial K} \right)}^{2}}Var(\widehat{K}) +{{\left( \frac{\partial \widehat{u}}{\partial n} \right)}^{2}}Var(\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial K} \right)Cov(\widehat{\beta },\widehat{K}) \\ & +2\left( \frac{\partial \widehat{u}}{\partial \beta } \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{\beta },\widehat{n}) +2\left( \frac{\partial \widehat{u}}{\partial K} \right)\left( \frac{\partial \widehat{u}}{\partial n} \right)Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} Var(\widehat{u})= & \frac{1}{{{\widehat{\beta }}^{4}}}{{\left[ \ln (-\ln (R)) \right]}^{2}}Var(\widehat{\beta })+\frac{1}{{{\widehat{K}}^{2}}}Var(\widehat{K}) +{{\left[ \ln (V) \right]}^{2}}Var(\widehat{n}) +\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}\widehat{K}}Cov(\widehat{\beta },\widehat{K}) \\ & +\frac{2\ln (-\ln (R))}{{{\widehat{\beta }}^{2}}}\ln (V)Cov(\widehat{\beta },\widehat{n}) +\frac{2\ln (V)}{\widehat{K}}Cov(\widehat{K},\widehat{n}) \end{align} }[/math]

The upper and lower bounds on time are then found by:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & {{e}^{{{u}_{U}}}} \\ & {{T}_{L}}= & {{e}^{{{u}_{L}}}} \end{align} }[/math]

Approximate Confidence Bounds on IPL-Lognormal

Bounds on the Parameters

Since the standard deviation, [math]\displaystyle{ {{\widehat{\sigma }}_{T}} }[/math] , and [math]\displaystyle{ \widehat{K} }[/math] are positive parameters, then [math]\displaystyle{ \ln ({{\widehat{\sigma }}_{{{T}'}}}) }[/math] and [math]\displaystyle{ \ln (\widehat{K}) }[/math] are treated as normally distributed, and the bounds are estimated from:

[math]\displaystyle{ \begin{align} {{\sigma }_{U}}=\ & {{\widehat{\sigma }}_{{{T}'}}}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}} &\text{ (Upper bound)} \\ {{\sigma }_{L}}=\ & \frac{{{\widehat{\sigma }}_{{{T}'}}}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}_{{{T}'}}})}}{{{\widehat{\sigma }}_{{{T}'}}}}}}} &\text{ (Lower bound)} \end{align} }[/math]

and:

[math]\displaystyle{ \begin{align} {{K}_{U}}=\ & \widehat{K}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}} &\text{ (Upper bound)} \\ {{K}_{L}}=\ & \frac{\widehat{K}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var(\widehat{K})}}{\widehat{K}}}}} &\text{ (Lower bound)} \end{align} }[/math]

The lower and upper bounds on [math]\displaystyle{ n }[/math] , are estimated from:

[math]\displaystyle{ \begin{align} & {{n}_{U}}= & \widehat{n}+{{K}_{\alpha }}\sqrt{Var(\widehat{n})}\text{ (Upper bound)} \\ & {{n}_{L}}= & \widehat{n}-{{K}_{\alpha }}\sqrt{Var(\widehat{n})}\text{ (Lower bound)} \end{align} }[/math]

The variances and covariances of [math]\displaystyle{ A, }[/math] [math]\displaystyle{ B, }[/math] and [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] are estimated from the local Fisher matrix (evaluated at [math]\displaystyle{ \widehat{A}, }[/math] [math]\displaystyle{ \widehat{B} }[/math] , [math]\displaystyle{ {{\widehat{\sigma }}_{{{T}'}}}), }[/math] as follows:

[math]\displaystyle{ \left[ \begin{matrix} Var({{\widehat{\sigma }}_{{{T}'}}}) & Cov(\widehat{K},{{\widehat{\sigma }}_{{{T}'}}}) & Cov(\widehat{n},{{\widehat{\sigma }}_{{{T}'}}}) \\ Cov({{\widehat{\sigma }}_{{{T}'}}},\widehat{K}) & Var(\widehat{K}) & Cov(\widehat{K},\widehat{n}) \\ Cov({{\widehat{\sigma }}_{{{T}'}}},\widehat{n}) & Cov(\widehat{n},\widehat{K}) & Var\left( \widehat{n} \right) \\ \end{matrix} \right]={{\left[ F \right]}^{-1}} }[/math]

where:

[math]\displaystyle{ F=\left[ \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial \sigma _{{{T}'}}^{2}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\sigma }_{{{T}'}}}\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{K}^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial K\partial n} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial {{\sigma }_{{{T}'}}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial n\partial K} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{n}^{2}}} \\ \end{matrix} \right] }[/math]

Bounds on Reliability

The reliability of the lognormal distribution is:

[math]\displaystyle{ R({T}',V;K,n,{{\sigma }_{{{T}'}}})=\int_{{{T}'}}^{\infty }\frac{1}{{{\widehat{\sigma }}_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}} \right)}^{2}}}}dt }[/math]

Let [math]\displaystyle{ \widehat{z}(t,V;K,n,{{\sigma }_{T}})=\tfrac{t+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}}, }[/math] then [math]\displaystyle{ \tfrac{d\widehat{z}}{dt}=\tfrac{1}{{{\widehat{\sigma }}_{{{T}'}}}}. }[/math]

For [math]\displaystyle{ t={T}' }[/math] , [math]\displaystyle{ \widehat{z}=\tfrac{{T}'+\ln (\widehat{K})+\widehat{n}\ln (V)}{{{\widehat{\sigma }}_{{{T}'}}}} }[/math] , and for [math]\displaystyle{ t=\infty , }[/math] [math]\displaystyle{ \widehat{z}=\infty . }[/math] The above equation then becomes:

[math]\displaystyle{ R(\widehat{z})=\int_{\widehat{z}({T}',V)}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz }[/math]

The bounds on [math]\displaystyle{ z }[/math] are estimated from:

[math]\displaystyle{ \begin{align} & {{z}_{U}}= & \widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \\ & {{z}_{L}}= & \widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \end{align} }[/math]

where:

.

[math]\displaystyle{ \begin{align} Var(\widehat{z})= & \left( \frac{\partial \widehat{z}}{\partial K} \right)_{\widehat{K}}^{2}Var(\widehat{K})+\left( \frac{\partial \widehat{z}}{\partial n} \right)_{\widehat{n}}^{2}Var(\widehat{n})+\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)_{{{\widehat{\sigma }}_{{{T}'}}}}^{2}Var({{\widehat{\sigma }}_{T}}) +2{{\left( \frac{\partial \widehat{z}}{\partial K} \right)}_{\widehat{K}}}{{\left( \frac{\partial \widehat{z}}{\partial n} \right)}_{\widehat{n}}}Cov\left( \widehat{K},\widehat{n} \right) \\ & +2{{\left( \frac{\partial \widehat{z}}{\partial K} \right)}_{\widehat{K}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{K},{{\widehat{\sigma }}_{T}} \right) +2{{\left( \frac{\partial \widehat{z}}{\partial n} \right)}_{\widehat{n}}}{{\left( \frac{\partial \widehat{z}}{\partial {{\sigma }_{{{T}'}}}} \right)}_{{{\widehat{\sigma }}_{{{T}'}}}}}Cov\left( \widehat{n},{{\widehat{\sigma }}_{T}} \right) \end{align} }[/math].

or:

[math]\displaystyle{ \begin{align} & Var(\widehat{z})= & \frac{1}{\widehat{\sigma }_{{{T}'}}^{2}}[\frac{1}{{{K}^{2}}}Var(\widehat{K})+\ln {{(V)}^{2}}Var(\widehat{n})+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +\frac{2\ln (V)}{K}Cov\left( \widehat{K},\widehat{n} \right)-\frac{2\widehat{z}}{K}Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right)-2\widehat{z}\ln (V)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right)] \end{align} }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & \int_{{{z}_{L}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Upper bound)} \\ & {{R}_{L}}= & \int_{{{z}_{U}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (Lower bound)} \end{align} }[/math]

Confidence Bounds on Time

The bounds around time, for a given lognormal percentile (unreliability), are estimated by first solving the reliability equation with respect to time, as follows:

[math]\displaystyle{ {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}})=-\ln (\widehat{K})-\widehat{n}\ln (V)+z\cdot {{\widehat{\sigma }}_{{{T}'}}} }[/math]

where:

[math]\displaystyle{ \begin{align} & {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}})=\ \ln (T) \\ \\ & z=\ {{\Phi }^{-1}}\left[ F({T}') \right] \end{align} }[/math]

and:

[math]\displaystyle{ \Phi (z)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{z({T}')}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz }[/math]

The next step is to calculate the variance of [math]\displaystyle{ {T}'(V;\widehat{K},\widehat{n},{{\widehat{\sigma }}_{{{T}'}}}): }[/math]

[math]\displaystyle{ \begin{align} Var({T}')= & {{\left( \frac{\partial {T}'}{\partial K} \right)}^{2}}Var(\widehat{K})+{{\left( \frac{\partial {T}'}{\partial n} \right)}^{2}}Var(\widehat{n})+{{\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +2\left( \frac{\partial {T}'}{\partial K} \right)\left( \frac{\partial {T}'}{\partial n} \right)Cov\left( \widehat{K},\widehat{n} \right) \\ & +2\left( \frac{\partial {T}'}{\partial K} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right) +2\left( \frac{\partial {T}'}{\partial n} \right)\left( \frac{\partial {T}'}{\partial {{\sigma }_{{{T}'}}}} \right)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} Var({T}')= & \frac{1}{{{K}^{2}}}Var(\widehat{K})+\ln {{(V)}^{2}}Var(\widehat{n})+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}_{{{T}'}}}) +\frac{2\ln (V)}{K}Cov\left( \widehat{K},\widehat{n} \right) \\ & -\frac{2\widehat{z}}{K}Cov\left( \widehat{K},{{\widehat{\sigma }}_{{{T}'}}} \right) -2\widehat{z}\ln (V)Cov\left( \widehat{n},{{\widehat{\sigma }}_{{{T}'}}} \right) \end{align} }[/math]

The upper and lower bounds are then found by:

[math]\displaystyle{ \begin{align} & T_{U}^{\prime }= & \ln {{T}_{U}}={T}'+{{K}_{\alpha }}\sqrt{Var({T}')} \\ & T_{L}^{\prime }= & \ln {{T}_{L}}={T}'-{{K}_{\alpha }}\sqrt{Var({T}')} \end{align} }[/math]

Solving for [math]\displaystyle{ {{T}_{U}} }[/math] and [math]\displaystyle{ {{T}_{L}} }[/math] yields:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & {{e}^{T_{U}^{\prime }}}\text{ (Upper bound)} \\ & {{T}_{L}}= & {{e}^{T_{L}^{\prime }}}\text{ (Lower bound)} \end{align} }[/math]