Template:Stress-Strength Confidence Intervals

Confidence Interval of the Probability

Both the stress and strenght distributions can be either estimated from actual data or specified by engineers based on engineering knowledge or existing references. Based on the sources of the distribution, there are two types of variations associated with the calculated probability.

Variation in Model Parameters

If both stress and strength distributions are estimated from data sets, then there are uncertainty associated with the estimated distribution parameters. These uncertainty will cause some degree of variation of the calculated probability from the stress-strength analysis. Therefore, we can use these uncertainty to estimate the confidence interval of the calculated probability. To get the confidence interval, we first calcualte the variance of the Reliablility using:

[math]\displaystyle{ Var\left[ R \right]=\int_{0}^{\infty }{Var\left[ {{f}_{1}}(x) \right]}{{\left[ {{R}_{2}}(x) \right]}^{2}}dx+{{\int_{0}^{\infty }{\left[ {{f}_{1}}(x) \right]}}^{2}}Var\left[ {{R}_{2}}(x) \right]dx }[/math]

Variance of [math]\displaystyle{ {{f}_{1}}(x) }[/math] and [math]\displaystyle{ {{R}_{2}}(x) }[/math] can be estimated from the Fisher Information Matrix. For detail, please see chapter Confidence Bounds.

Once the variance of the expected reliability is obtained, the two-sided confidence interval of it can be calcualted using:

[math]\displaystyle{ [\frac{R}{R+(1-R)w},\frac{R}{R+(1-R)/w}] }[/math]

where:

CL is the confidence level;

[math]\displaystyle{ \alpha }[/math] = 1-CL;

[math]\displaystyle{ w=\exp \{{{z}_{1-\alpha /2}}\sqrt{Var(R)}/[R(1-R)]\} }[/math];

[math]\displaystyle{ {{Z}_{1-\alpha /2}} }[/math] is the [math]\displaystyle{ 1-\alpha/2 }[/math] percential of a standard normal distribution.

If the upper bound (U) and lower bound (L) are not infinite and 0, the above calcualted variance of R is adjusted by [math]\displaystyle{ {{\left[ {1}/{\left( {{F}_{1}}(U)-{{F}_{1}}(L) \right)}\; \right]}^{2}} }[/math].

Variation in Probability Values

Assume the distributions for stress and strength are known. From the stress-strength equation:

[math]\displaystyle{ R=P[Stress\le Strength]=\int_{0}^{\infty }{{{f}_{Stress}}(x)\cdot {{R}_{Strength}}(x)}dx }[/math]

we know, the calcualted reliability is the Expected value of the probability that a strength value is larger than a stress value. Since both strength and stress are random variables from their distributions, the reliability is also a random variable. This can be explained using the following exampe. Let's first assume stress is a fixed value of 567. The reliability then is:

[math]\displaystyle{ R(567)=\Pr (Strength\gt 567)={{R}_{2}}(567) }[/math]

This is the reliability when the stress value is 567 and when the strength distribution is given. If stress is not a fixed value, instead it follows a distribution, then it can take values other than 567. For instance, it can be a value of 700. Therefore, we get another reliability value of [math]\displaystyle{ {R}(700) }[/math]. Since stress is a random variable, for any stress value [math]\displaystyle{ {x}_{i} }[/math], there is a reliability value of [math]\displaystyle{ R({{x}_{i}}) }[/math] calculated from the strength distribution. We will end up with many [math]\displaystyle{ R({{x}_{i}}) }[/math]s or [math]\displaystyle{ R_{2}({{x}_{i}}) }[/math]s. From these [math]\displaystyle{ R({{x}_{i}}) }[/math]s, we can get the mean and variance of the reliability. In fact, its mean is the the result from:

[math]\displaystyle{ R=P[Stress\le Strength]=\int_{0}^{\infty }{{{f}_{Stress}}(x)\cdot {{R}_{Strength}}(x)}dx }[/math]

and its variacne is:

[math]\displaystyle{ \begin{align} & Var\left[ R \right]=Var\left[ {{R}_{2}}({{X}_{1}}) \right]=E\left[ {{R}_{2}}{{\left( {{X}_{1}} \right)}^{2}} \right]-{{\left( E\left[ {{R}_{2}}\left( {{X}_{1}} \right) \right] \right)}^{2}} \\ & =\int_{0}^{\infty }{{{f}_{1}}(x){{\left[ {{R}_{2}}(x) \right]}^{2}}dx}-{{\left( E\left[ {{R}_{2}}\left( {{X}_{1}} \right) \right] \right)}^{2}} \\ & =\int_{0}^{\infty }{{{f}_{1}}(x){{\left[ {{R}_{2}}(x) \right]}^{2}}dx}-{{\left( R \right)}^{2}} \\ \end{align} }[/math]

where R is the expected value of the reliability.

Once the variance of the expected reliability is obtained, the two-sided confidence interval of it can be calcualted using:

[math]\displaystyle{ [\frac{R}{R+(1-R)w},\frac{R}{R+(1-R)/w}] }[/math]

where:

CL is the confidence level;

[math]\displaystyle{ \alpha }[/math] = 1-CL;

[math]\displaystyle{ w=\exp \{{{z}_{1-\alpha /2}}\sqrt{Var(R)}/[R(1-R)]\} }[/math];

[math]\displaystyle{ {{Z}_{1-\alpha /2}} }[/math] is the [math]\displaystyle{ 1-\alpha/2 }[/math] percential of a standard normal distribution.

If the upper bound (U) and lower bound (L) are not infinite and 0, the above calcualted variance of R is adjusted by [math]\displaystyle{ {{\left[ {1}/{\left( {{F}_{1}}(U)-{{F}_{1}}(L) \right)}\; \right]}^{2}} }[/math].

Example 1:

Assume that the stress distribution for a component is known to be a Weibull distribution with beta = 3 and eta = 2000. For the current design, the strength distribution is also a Weibull distribution with beta =1.5 and eta=4000. Evaluate the current reliability of the component. If the reliability does not meet the target reliability of 90%, determine what parameters would be required for the strength distribution in order to meet the specified target.

Solution

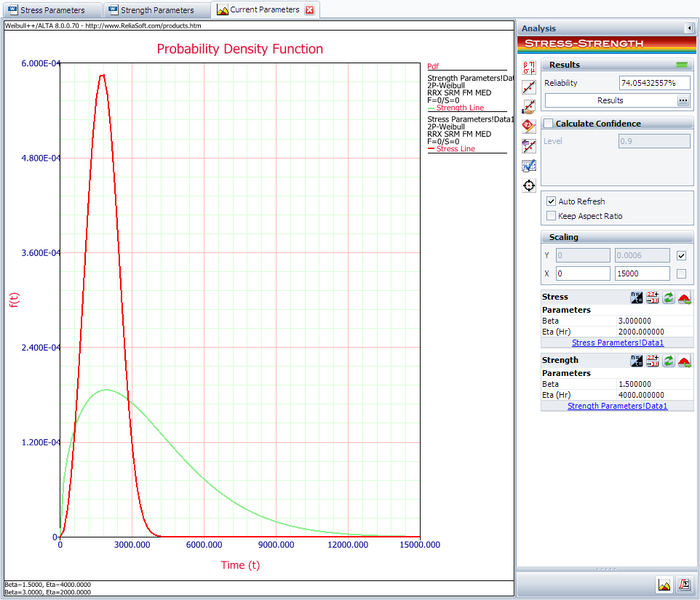
The following picture shows the stress-strength tool and the calculated reliability of the current design.

The result shows that the current reliability is about 74.0543%, which is below the target value of 90%. We need to use the Target Reliability Parameter Estimator to determine the parameters for the strength distribution that, when compared against the stress distribution, would result in the target reliability.

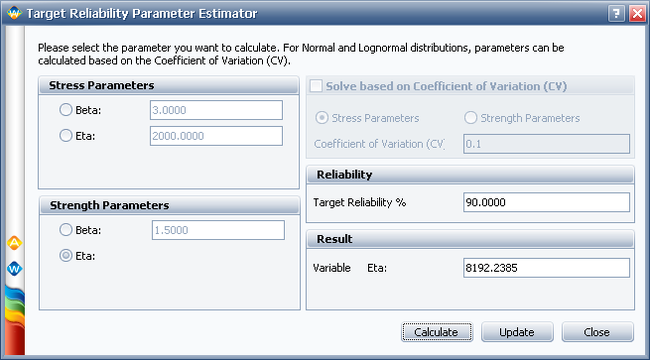
The following picture shows the Target Reliability Parameter Estimator window. In the Strength Parameters area, select eta. Set the Target Reliability to 90% and click Calculate. The calculated eta is 8192.2385 hours.

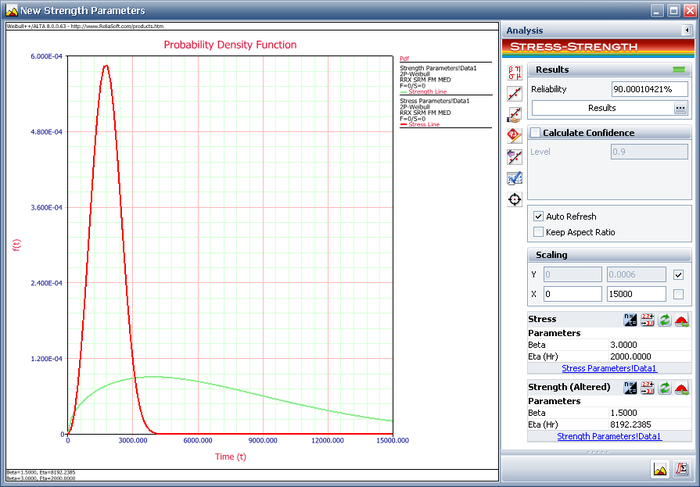
Click Update to perform the stress-strength analysis again using the altered parameters for the strength distribution. The following plot shows that the calculated reliability is 90%. Therefore, in order to meet the reliability requirement, the component must be redesigned such that the eta parameter of the strength distribution is at least 8192.2385 hours.