Template:Non-parametric LDA confidence bounds
Non-parametric Confidence Bounds
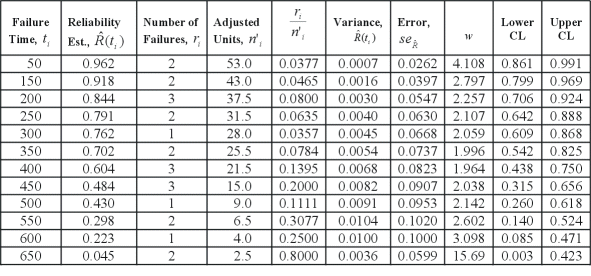
Confidence bounds for nonparametric reliability estimates can be calculated using a method similar to that of parametric confidence bounds. The difficulty in dealing with nonparametric data lies in the estimation of the variance. To estimate the variance for nonparametric data, Weibull++ uses Greenwood's formula [27]:
- [math]\displaystyle{ \widehat{Var}(\widehat{R}({{t}_{i}}))={{\left[ \widehat{R}({{t}_{i}}) \right]}^{2}}\cdot \underset{j=1}{\overset{i}{\mathop \sum }}\,\frac{\tfrac{{{r}_{j}}}{{{n}_{j}}}}{{{n}_{j}}\cdot \left( 1-\tfrac{{{r}_{j}}}{{{n}_{j}}} \right)} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & m= & \text{ the total number of intervals} \\ & n= & \text{ the total number of units} \end{align} }[/math]
The variable [math]\displaystyle{ {{n}_{i}} }[/math] is defined by:
- [math]\displaystyle{ {{n}_{i}}=n-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{s}_{j}}-\underset{j=0}{\overset{i-1}{\mathop \sum }}\,{{r}_{j,}}\text{ }i=1,...,m }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{r}_{j}}= & \text{the number of failures in interval }j \\ & {{s}_{j}}= & \text{the number of suspensions in interval }j \end{align} }[/math]
Once the variance has been calculated, the standard error can be determined by taking the square root of the variance:
- [math]\displaystyle{ {{\widehat{se}}_{\widehat{R}}}=\sqrt{\widehat{Var}(\widehat{R}({{t}_{i}}))} }[/math]
This information can then be applied to determine the confidence bounds:
- [math]\displaystyle{ \left[ LC{{B}_{\widehat{R}}},\text{ }UC{{B}_{\widehat{R}}} \right]=\left[ \frac{\widehat{R}}{\widehat{R}+(1-\widehat{R})\cdot w},\text{ }\frac{\widehat{R}}{\widehat{R}+(1-\widehat{R})/w} \right] }[/math]
- where:
- [math]\displaystyle{ w={{e}^{{{z}_{\alpha }}\cdot \tfrac{{{\widehat{se}}_{\widehat{R}}}}{\left[ \widehat{R}\cdot (1-\widehat{R}) \right]}}} }[/math]
and [math]\displaystyle{ \alpha }[/math] is the desired confidence level for the 1-sided confidence bounds.
Example 12
Determine the 1-sided confidence bounds for the reliability estimates in Example 11, with a 95% confidence level.
Solution to Example 12
Once again, this type of problem is most readily solved by constructing a table similar to the following:
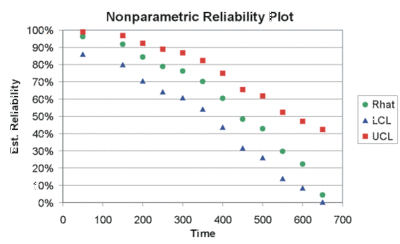
The following plot illustrates these results graphically: