Template:Lognormal distribution Likelihood ratio confidence bounds

Likelihood Ratio Confidence Bounds

Bounds on Parameters

As covered in Chapter Parameter Estimation, the likelihood confidence bounds are calculated by finding values for [math]\displaystyle{ {{\theta }_{1}} }[/math] and [math]\displaystyle{ {{\theta }_{2}} }[/math] that satisfy:

[math]\displaystyle{ -2\cdot \text{ln}\left( \frac{L({{\theta }_{1}},{{\theta }_{2}})}{L({{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}})} \right)=\chi _{\alpha ;1}^{2} }[/math]

This equation can be rewritten as:

[math]\displaystyle{ L({{\theta }_{1}},{{\theta }_{2}})=L({{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}})\cdot {{e}^{\tfrac{-\chi _{\alpha ;1}^{2}}{2}}} }[/math]

For complete data, the likelihood formula for the normal distribution is given by:

[math]\displaystyle{ L({\mu }',{{\sigma' }})=\underset{i=1}{\overset{N}{\mathop \prod }}\,f({{x}_{i}};{\mu }',{{\sigma' }})=\underset{i=1}{\overset{N}{\mathop \prod }}\,\frac{1}{{{x}_{i}}\cdot {{\sigma' }}\cdot \sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( \tfrac{\text{ln}({{x}_{i}})-{\mu }'}{{{\sigma'}}} \right)}^{2}}}} }[/math]

where the [math]\displaystyle{ {{x}_{i}} }[/math] values represent the original time-to-failure data. For a given value of [math]\displaystyle{ \alpha }[/math] , values for [math]\displaystyle{ {\mu }' }[/math] and [math]\displaystyle{ {{\sigma' }} }[/math] can be found which represent the maximum and minimum values that satisfy likelihood ratio equation. These represent the confidence bounds for the parameters at a confidence level [math]\displaystyle{ \delta , }[/math] where [math]\displaystyle{ \alpha =\delta }[/math] for two-sided bounds and [math]\displaystyle{ \alpha =2\delta -1 }[/math] for one-sided.

Example 5:

The lognormal distribution is commonly used to model the lives of units whose failure modes are of a fatigue-stress nature. Since this includes most, if not all, mechanical systems, the lognormal distribution can have widespread application. Consequently, the lognormal distribution is a good companion to the Weibull distribution when attempting to model these types of units. As may be surmised by the name, the lognormal distribution has certain similarities to the normal distribution. A random variable is lognormally distributed if the logarithm of the random variable is normally distributed. Because of this, there are many mathematical similarities between the two distributions. For example, the mathematical reasoning for the construction of the probability plotting scales and the bias of parameter estimators is very similar for these two distributions.

Lognormal Probability Density Function

The lognormal distribution is a 2-parameter distribution with parameters [math]\displaystyle{ {\mu }'\,\! }[/math] and [math]\displaystyle{ \sigma'\,\! }[/math]. The pdf for this distribution is given by:

[math]\displaystyle{ f({t}')=\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{t}^{\prime }}-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}\,\! }[/math]

where:

[math]\displaystyle{ {t}'=\ln (t)\,\! }[/math]. [math]\displaystyle{ t\,\! }[/math] values are the times-to-failure

[math]\displaystyle{ \mu'\,\! }[/math] = mean of the natural logarithms of the times-to-failure

[math]\displaystyle{ \sigma'\,\! }[/math] = standard deviation of the natural logarithms of the times-to-failure

The lognormal pdf can be obtained, realizing that for equal probabilities under the normal and lognormal pdfs, incremental areas should also be equal, or:

[math]\displaystyle{ \begin{align} f(t)dt=f({t}')d{t}' \end{align}\,\! }[/math]

Taking the derivative of the relationship between [math]\displaystyle{ {t}'\,\! }[/math] and [math]\displaystyle{ {t}\,\! }[/math] yields:

[math]\displaystyle{ d{t}'=\frac{dt}{t}\,\! }[/math]

Substitution yields:

[math]\displaystyle{ \begin{align} f(t)= & \frac{f({t}')}{t} \\ f(t)= & \frac{1}{t\cdot {{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{\text{ln}(t)-{\mu }'}{{{\sigma' }}} \right)}^{2}}}} \end{align}\,\! }[/math]

where:

[math]\displaystyle{ f(t)\ge 0,t\gt 0,-\infty \lt {\mu }'\lt \infty ,{{\sigma' }}\gt 0\,\! }[/math]

Lognormal Distribution Functions

The Mean or MTTF

The mean of the lognormal distribution, [math]\displaystyle{ \mu \,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ \mu ={{e}^{{\mu }'+\tfrac{1}{2}\sigma'^{2}}}\,\! }[/math]

The mean of the natural logarithms of the times-to-failure, [math]\displaystyle{ \mu'\,\! }[/math], in terms of [math]\displaystyle{ \bar{T}\,\! }[/math] and [math]\displaystyle{ {{\sigma}}\,\! }[/math] is given by:

[math]\displaystyle{ {\mu }'=\ln \left( {\bar{T}} \right)-\frac{1}{2}\ln \left( \frac{\sigma^{2}}{{{{\bar{T}}}^{2}}}+1 \right)\,\! }[/math]

The Median

The median of the lognormal distribution, [math]\displaystyle{ \breve{T}\,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ \breve{T}={{e}^{{{\mu}'}}}\,\! }[/math]

The Mode

The mode of the lognormal distribution, [math]\displaystyle{ \tilde{T}\,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ \tilde{T}={{e}^{{\mu }'-\sigma'^{2}}}\,\! }[/math]

The Standard Deviation

The standard deviation of the lognormal distribution, [math]\displaystyle{ {\sigma }_{T}\,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ {\sigma}_{T} =\sqrt{\left( {{e}^{2\mu '+\sigma {{'}^{2}}}} \right)\left( {{e}^{\sigma {{'}^{2}}}}-1 \right)}\,\! }[/math]

The standard deviation of the natural logarithms of the times-to-failure, [math]\displaystyle{ {\sigma}'\,\! }[/math], in terms of [math]\displaystyle{ \bar{T}\,\! }[/math] and [math]\displaystyle{ {\sigma}\,\! }[/math] is given by:

[math]\displaystyle{ \sigma '=\sqrt{\ln \left( \frac{{\sigma}_{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)}\,\! }[/math]

The Lognormal Reliability Function

The reliability for a mission of time [math]\displaystyle{ t\,\! }[/math], starting at age 0, for the lognormal distribution is determined by:

[math]\displaystyle{ R(t)=\int_{t}^{\infty }f(x)dx\,\! }[/math]

or:

[math]\displaystyle{ {{R}({t})}=\int_{\text{ln}(t)}^{\infty }\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx\,\! }[/math]

As with the normal distribution, there is no closed-form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability we will not discuss manual solution methods. For interested readers, full explanations can be found in the references.

The Lognormal Conditional Reliability Function

The lognormal conditional reliability function is given by:

[math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)}=\frac{\int_{\text{ln}(T+t)}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}ds}{\int_{\text{ln}(T)}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx}\,\! }[/math]

Once again, the use of standard normal tables is necessary to solve this equation, as no closed-form solution exists.

The Lognormal Reliable Life Function

As there is no closed-form solution for the lognormal reliability equation, no closed-form solution exists for the lognormal reliable life either. In order to determine this value, one must solve the following equation for [math]\displaystyle{ t\,\! }[/math]:

[math]\displaystyle{ {{R}_{t}}=\int_{\text{ln}(t)}^{\infty }\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx\,\! }[/math]

The Lognormal Failure Rate Function

The lognormal failure rate is given by:

[math]\displaystyle{ \lambda (t)=\frac{f(t)}{R(t)}=\frac{\tfrac{1}{t\cdot {{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{{t}'-{\mu }'}{{{\sigma' }}})}^{2}}}}}{\int_{{{t}'}}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{x-{\mu }'}{{{\sigma' }}})}^{2}}}}dx}\,\! }[/math]

As with the reliability equations, standard normal tables will be required to solve for this function.

Characteristics of the Lognormal Distribution

• The lognormal distribution is a distribution skewed to the right.
• The pdf starts at zero, increases to its mode, and decreases thereafter.
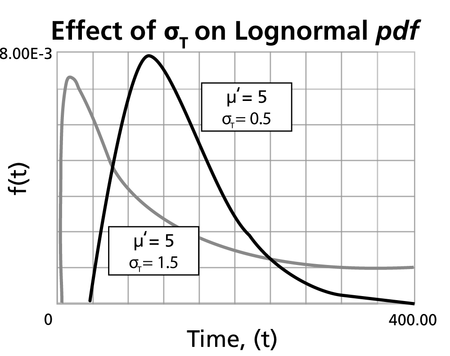
• The degree of skewness increases as [math]\displaystyle{ {{\sigma'}}\,\! }[/math] increases, for a given [math]\displaystyle{ \mu'\,\! }[/math]

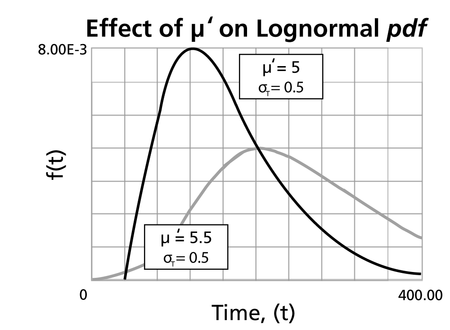
• For the same [math]\displaystyle{ {{\sigma'}}\,\! }[/math], the pdf 's skewness increases as [math]\displaystyle{ {\mu }'\,\! }[/math] increases.
• For [math]\displaystyle{ {{\sigma' }}\,\! }[/math] values significantly greater than 1, the pdf rises very sharply in the beginning, (i.e., for very small values of [math]\displaystyle{ T\,\! }[/math] near zero), and essentially follows the ordinate axis, peaks out early, and then decreases sharply like an exponential pdf or a Weibull pdf with [math]\displaystyle{ 0\lt \beta \lt 1\,\! }[/math].
• The parameter, [math]\displaystyle{ {\mu }'\,\! }[/math], in terms of the logarithm of the [math]\displaystyle{ {T}'s\,\! }[/math] is also the scale parameter, and not the location parameter as in the case of the normal pdf.
• The parameter [math]\displaystyle{ {{\sigma'}}\,\! }[/math], or the standard deviation of the [math]\displaystyle{ {T}'s\,\! }[/math] in terms of their logarithm or of their [math]\displaystyle{ {T}'\,\! }[/math], is also the shape parameter and not the scale parameter, as in the normal pdf, and assumes only positive values.

Lognormal Distribution Parameters in ReliaSoft's Software

In ReliaSoft's software, the parameters returned for the lognormal distribution are always logarithmic. That is: the parameter [math]\displaystyle{ {\mu }'\,\! }[/math] represents the mean of the natural logarithms of the times-to-failure, while [math]\displaystyle{ {{\sigma' }}\,\! }[/math] represents the standard deviation of these data point logarithms. Specifically, the returned [math]\displaystyle{ {{\sigma' }}\,\! }[/math] is the square root of the variance of the natural logarithms of the data points. Even though the application denotes these values as mean and standard deviation, the user is reminded that these are given as the parameters of the distribution, and are thus the mean and standard deviation of the natural logarithms of the data. The mean value of the times-to-failure, not used as a parameter, as well as the standard deviation can be obtained through the QCP or the Function Wizard.

Lognormal Distribution Examples

Complete Data Example

Determine the lognormal parameter estimates for the data given in the following table.

Non-Grouped Times-to-Failure Data
Data point index	State F or S	State End Time
1	F	2
2	F	5
3	F	11
4	F	23
5	F	29
6	F	37
7	F	43
8	F	59

Solution

Using Weibull++, the computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 2.83 \\ & {\hat{\sigma '}}= & 1.10 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ X\,\! }[/math]

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 2.83 \\ & {{{\hat{\sigma' }}}}= & 1.24 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ Y:\,\! }[/math]

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 2.83 \\ & {{{\hat{\sigma' }}}}= & 1.36 \end{align}\,\! }[/math]

Complete Data RRX Example

From Kececioglu [20, p. 347]. 15 identical units were tested to failure and following is a table of their failure times:

Times-to-Failure Data [math]\displaystyle{ \begin{matrix} \text{Data Point Index} & \text{Failure Times (Hr)} \\ \text{1} & \text{62}\text{.5} \\ \text{2} & \text{91}\text{.9} \\ \text{3} & \text{100}\text{.3} \\ \text{4} & \text{117}\text{.4} \\ \text{5} & \text{141}\text{.1} \\ \text{6} & \text{146}\text{.8} \\ \text{7} & \text{172}\text{.7} \\ \text{8} & \text{192}\text{.5} \\ \text{9} & \text{201}\text{.6} \\ \text{10} & \text{235}\text{.8} \\ \text{11} & \text{249}\text{.2} \\ \text{12} & \text{297}\text{.5} \\ \text{13} & \text{318}\text{.3} \\ \text{14} & \text{410}\text{.6} \\ \text{15} & \text{550}\text{.5} \\ \end{matrix}\,\! }[/math]

Solution

Published results (using probability plotting):

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=5.22575 \\ {{\widehat{\sigma' }}}=0.62048. \\ \end{matrix}\,\! }[/math]

Weibull++ computed parameters for rank regression on X are:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=5.2303 \\ {{\widehat{\sigma'}}}=0.6283. \\ \end{matrix}\,\! }[/math]

The small differences are due to the precision errors when fitting a line manually, whereas in Weibull++ the line was fitted mathematically.

Complete Data Unbiased MLE Example

From Kececioglu [19, p. 406]. 9 identical units are tested continuously to failure and failure times were recorded at 30.4, 36.7, 53.3, 58.5, 74.0, 99.3, 114.3, 140.1 and 257.9 hours.

Solution

The results published were obtained by using the unbiased model. Published Results (using MLE):

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=4.3553 \\ {{\widehat{\sigma' }}}=0.67677 \\ \end{matrix}\,\! }[/math]

This same data set can be entered into Weibull++ by creating a data sheet capable of handling non-grouped time-to-failure data. Since the results shown above are unbiased, the Use Unbiased Std on Normal Data option in the User Setup must be selected in order to duplicate these results. Weibull++ computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=4.3553 \\ {{\widehat{\sigma' }}}=0.6768 \\ \end{matrix}\,\! }[/math]

Suspension Data Example

From Nelson [30, p. 324]. 96 locomotive controls were tested, 37 failed and 59 were suspended after running for 135,000 miles. The table below shows the failure and suspension times.

Nelson's Locomotive Data
	Number in State	F or S	Time
1	1	F	22.5
2	1	F	37.5
3	1	F	46
4	1	F	48.5
5	1	F	51.5
6	1	F	53
7	1	F	54.5
8	1	F	57.5
9	1	F	66.5
10	1	F	68
11	1	F	69.5
12	1	F	76.5
13	1	F	77
14	1	F	78.5
15	1	F	80
16	1	F	81.5
17	1	F	82
18	1	F	83
19	1	F	84
20	1	F	91.5
21	1	F	93.5
22	1	F	102.5
23	1	F	107
24	1	F	108.5
25	1	F	112.5
26	1	F	113.5
27	1	F	116
28	1	F	117
29	1	F	118.5
30	1	F	119
31	1	F	120
32	1	F	122.5
33	1	F	123
34	1	F	127.5
35	1	F	131
36	1	F	132.5
37	1	F	134
38	59	S	135

Solution

The distribution used in the publication was the base-10 lognormal. Published results (using MLE):

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=2.2223 \\ {{\widehat{\sigma' }}}=0.3064 \\ \end{matrix}\,\! }[/math]

Published 95% confidence limits on the parameters:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=\left\{ 2.1336,2.3109 \right\} \\ {{\widehat{\sigma'}}}=\left\{ 0.2365,0.3970 \right\} \\ \end{matrix}\,\! }[/math]

Published variance/covariance matrix:

[math]\displaystyle{ \left[ \begin{matrix} \widehat{Var}\left( {{{\hat{\mu }}}^{\prime }} \right)=0.0020 & {} & \widehat{Cov}({{{\hat{\mu }}}^{\prime }},{{{\hat{\sigma' }}}})=0.001 \\ {} & {} & {} \\ \widehat{Cov}({{{\hat{\mu }}}^{\prime }},{{{\hat{\sigma' }}}})=0.001 & {} & \widehat{Var}\left( {{{\hat{\sigma '}}}} \right)=0.0016 \\ \end{matrix} \right]\,\! }[/math]

To replicate the published results (since Weibull++ uses a lognormal to the base [math]\displaystyle{ e\,\! }[/math] ), take the base-10 logarithm of the data and estimate the parameters using the normal distribution and MLE.

• Weibull++ computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=2.2223 \\ {{\widehat{\sigma' }}}=0.3064 \\ \end{matrix}\,\! }[/math]

• Weibull++ computed 95% confidence limits on the parameters:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=\left\{ 2.1364,2.3081 \right\} \\ {{\widehat{\sigma'}}}=\left\{ 0.2395,0.3920 \right\} \\ \end{matrix}\,\! }[/math]

• Weibull++ computed/variance covariance matrix:

[math]\displaystyle{ \left[ \begin{matrix} \widehat{Var}\left( {{{\hat{\mu }}}^{\prime }} \right)=0.0019 & {} & \widehat{Cov}({{{\hat{\mu }}}^{\prime }},{{{\hat{\sigma' }}}})=0.0009 \\ {} & {} & {} \\ \widehat{Cov}({\mu }',{{{\hat{\sigma' }}}})=0.0009 & {} & \widehat{Var}\left( {{{\hat{\sigma' }}}} \right)=0.0015 \\ \end{matrix} \right]\,\! }[/math]

Interval Data Example

Determine the lognormal parameter estimates for the data given in the table below.

Non-Grouped Data Times-to-Failure with Intervals
Data point index	Last Inspected	State End Time
1	30	32
2	32	35
3	35	37
4	37	40
5	42	42
6	45	45
7	50	50
8	55	55

Solution

This is a sequence of interval times-to-failure where the intervals vary substantially in length. Using Weibull++, the computed parameters for maximum likelihood are calculated to be:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 3.64 \\ & {{{\hat{\sigma' }}}}= & 0.18 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ X\ \,\! }[/math]:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 3.64 \\ & {{{\hat{\sigma' }}}}= & 0.17 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ Y\ \,\! }[/math]:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 3.64 \\ & {{{\hat{\sigma' }}}}= & 0.21 \end{align}\,\! }[/math]

Bounds on Time and Reliability

In order to calculate the bounds on a time estimate for a given reliability, or on a reliability estimate for a given time, the likelihood function needs to be rewritten in terms of one parameter and time/reliability, so that the maximum and minimum values of the time can be observed as the parameter is varied. This can be accomplished by substituting a form of the normal reliability equation into the likelihood function. The normal reliability equation can be written as:

[math]\displaystyle{ R=1-\Phi \left( \frac{\text{ln}(t)-{\mu }'}{{{\sigma'}}} \right) }[/math]

This can be rearranged to the form:

[math]\displaystyle{ {\mu }'=\text{ln}(t)-{{\sigma'}}\cdot {{\Phi }^{-1}}(1-R) }[/math]

where [math]\displaystyle{ {{\Phi }^{-1}} }[/math] is the inverse standard normal. This equation can now be substituted into likelihood function to produce a likelihood equation in terms of [math]\displaystyle{ {{\sigma'}}, }[/math] [math]\displaystyle{ t }[/math] and [math]\displaystyle{ R }[/math]:

[math]\displaystyle{ L({{\sigma'}},t/R)=\underset{i=1}{\overset{N}{\mathop \prod }}\,\frac{1}{{{x}_{i}}\cdot {{\sigma'}}\cdot \sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( \tfrac{\text{ln}({{x}_{i}})-\left( \text{ln}(t)-{{\sigma'}}\cdot {{\Phi }^{-1}}(1-R) \right)}{{{\sigma'}}} \right)}^{2}}}} }[/math]

The unknown variable [math]\displaystyle{ t/R }[/math] depends on what type of bounds are being determined. If one is trying to determine the bounds on time for a given reliability, then [math]\displaystyle{ R }[/math] is a known constant and [math]\displaystyle{ t }[/math] is the unknown variable. Conversely, if one is trying to determine the bounds on reliability for a given time, then [math]\displaystyle{ t }[/math] is a known constant and [math]\displaystyle{ R }[/math] is the unknown variable. Either way, the above equation can be used to solve the likelihood ratio equation for the values of interest.

Example 6:

The lognormal distribution is commonly used to model the lives of units whose failure modes are of a fatigue-stress nature. Since this includes most, if not all, mechanical systems, the lognormal distribution can have widespread application. Consequently, the lognormal distribution is a good companion to the Weibull distribution when attempting to model these types of units. As may be surmised by the name, the lognormal distribution has certain similarities to the normal distribution. A random variable is lognormally distributed if the logarithm of the random variable is normally distributed. Because of this, there are many mathematical similarities between the two distributions. For example, the mathematical reasoning for the construction of the probability plotting scales and the bias of parameter estimators is very similar for these two distributions.

Lognormal Probability Density Function

The lognormal distribution is a 2-parameter distribution with parameters [math]\displaystyle{ {\mu }'\,\! }[/math] and [math]\displaystyle{ \sigma'\,\! }[/math]. The pdf for this distribution is given by:

[math]\displaystyle{ f({t}')=\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{t}^{\prime }}-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}\,\! }[/math]

where:

[math]\displaystyle{ {t}'=\ln (t)\,\! }[/math]. [math]\displaystyle{ t\,\! }[/math] values are the times-to-failure

[math]\displaystyle{ \mu'\,\! }[/math] = mean of the natural logarithms of the times-to-failure

[math]\displaystyle{ \sigma'\,\! }[/math] = standard deviation of the natural logarithms of the times-to-failure

The lognormal pdf can be obtained, realizing that for equal probabilities under the normal and lognormal pdfs, incremental areas should also be equal, or:

[math]\displaystyle{ \begin{align} f(t)dt=f({t}')d{t}' \end{align}\,\! }[/math]

Taking the derivative of the relationship between [math]\displaystyle{ {t}'\,\! }[/math] and [math]\displaystyle{ {t}\,\! }[/math] yields:

[math]\displaystyle{ d{t}'=\frac{dt}{t}\,\! }[/math]

Substitution yields:

[math]\displaystyle{ \begin{align} f(t)= & \frac{f({t}')}{t} \\ f(t)= & \frac{1}{t\cdot {{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{\text{ln}(t)-{\mu }'}{{{\sigma' }}} \right)}^{2}}}} \end{align}\,\! }[/math]

where:

[math]\displaystyle{ f(t)\ge 0,t\gt 0,-\infty \lt {\mu }'\lt \infty ,{{\sigma' }}\gt 0\,\! }[/math]

Lognormal Distribution Functions

The Mean or MTTF

The mean of the lognormal distribution, [math]\displaystyle{ \mu \,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ \mu ={{e}^{{\mu }'+\tfrac{1}{2}\sigma'^{2}}}\,\! }[/math]

The mean of the natural logarithms of the times-to-failure, [math]\displaystyle{ \mu'\,\! }[/math], in terms of [math]\displaystyle{ \bar{T}\,\! }[/math] and [math]\displaystyle{ {{\sigma}}\,\! }[/math] is given by:

[math]\displaystyle{ {\mu }'=\ln \left( {\bar{T}} \right)-\frac{1}{2}\ln \left( \frac{\sigma^{2}}{{{{\bar{T}}}^{2}}}+1 \right)\,\! }[/math]

The Median

The median of the lognormal distribution, [math]\displaystyle{ \breve{T}\,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ \breve{T}={{e}^{{{\mu}'}}}\,\! }[/math]

The Mode

The mode of the lognormal distribution, [math]\displaystyle{ \tilde{T}\,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ \tilde{T}={{e}^{{\mu }'-\sigma'^{2}}}\,\! }[/math]

The Standard Deviation

The standard deviation of the lognormal distribution, [math]\displaystyle{ {\sigma }_{T}\,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ {\sigma}_{T} =\sqrt{\left( {{e}^{2\mu '+\sigma {{'}^{2}}}} \right)\left( {{e}^{\sigma {{'}^{2}}}}-1 \right)}\,\! }[/math]

The standard deviation of the natural logarithms of the times-to-failure, [math]\displaystyle{ {\sigma}'\,\! }[/math], in terms of [math]\displaystyle{ \bar{T}\,\! }[/math] and [math]\displaystyle{ {\sigma}\,\! }[/math] is given by:

[math]\displaystyle{ \sigma '=\sqrt{\ln \left( \frac{{\sigma}_{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)}\,\! }[/math]

The Lognormal Reliability Function

The reliability for a mission of time [math]\displaystyle{ t\,\! }[/math], starting at age 0, for the lognormal distribution is determined by:

[math]\displaystyle{ R(t)=\int_{t}^{\infty }f(x)dx\,\! }[/math]

or:

[math]\displaystyle{ {{R}({t})}=\int_{\text{ln}(t)}^{\infty }\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx\,\! }[/math]

As with the normal distribution, there is no closed-form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability we will not discuss manual solution methods. For interested readers, full explanations can be found in the references.

The Lognormal Conditional Reliability Function

The lognormal conditional reliability function is given by:

[math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)}=\frac{\int_{\text{ln}(T+t)}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}ds}{\int_{\text{ln}(T)}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx}\,\! }[/math]

Once again, the use of standard normal tables is necessary to solve this equation, as no closed-form solution exists.

The Lognormal Reliable Life Function

As there is no closed-form solution for the lognormal reliability equation, no closed-form solution exists for the lognormal reliable life either. In order to determine this value, one must solve the following equation for [math]\displaystyle{ t\,\! }[/math]:

[math]\displaystyle{ {{R}_{t}}=\int_{\text{ln}(t)}^{\infty }\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx\,\! }[/math]

The Lognormal Failure Rate Function

The lognormal failure rate is given by:

[math]\displaystyle{ \lambda (t)=\frac{f(t)}{R(t)}=\frac{\tfrac{1}{t\cdot {{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{{t}'-{\mu }'}{{{\sigma' }}})}^{2}}}}}{\int_{{{t}'}}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{x-{\mu }'}{{{\sigma' }}})}^{2}}}}dx}\,\! }[/math]

As with the reliability equations, standard normal tables will be required to solve for this function.

Characteristics of the Lognormal Distribution

• The lognormal distribution is a distribution skewed to the right.
• The pdf starts at zero, increases to its mode, and decreases thereafter.
• The degree of skewness increases as [math]\displaystyle{ {{\sigma'}}\,\! }[/math] increases, for a given [math]\displaystyle{ \mu'\,\! }[/math]

• For the same [math]\displaystyle{ {{\sigma'}}\,\! }[/math], the pdf 's skewness increases as [math]\displaystyle{ {\mu }'\,\! }[/math] increases.
• For [math]\displaystyle{ {{\sigma' }}\,\! }[/math] values significantly greater than 1, the pdf rises very sharply in the beginning, (i.e., for very small values of [math]\displaystyle{ T\,\! }[/math] near zero), and essentially follows the ordinate axis, peaks out early, and then decreases sharply like an exponential pdf or a Weibull pdf with [math]\displaystyle{ 0\lt \beta \lt 1\,\! }[/math].
• The parameter, [math]\displaystyle{ {\mu }'\,\! }[/math], in terms of the logarithm of the [math]\displaystyle{ {T}'s\,\! }[/math] is also the scale parameter, and not the location parameter as in the case of the normal pdf.
• The parameter [math]\displaystyle{ {{\sigma'}}\,\! }[/math], or the standard deviation of the [math]\displaystyle{ {T}'s\,\! }[/math] in terms of their logarithm or of their [math]\displaystyle{ {T}'\,\! }[/math], is also the shape parameter and not the scale parameter, as in the normal pdf, and assumes only positive values.

Lognormal Distribution Parameters in ReliaSoft's Software

In ReliaSoft's software, the parameters returned for the lognormal distribution are always logarithmic. That is: the parameter [math]\displaystyle{ {\mu }'\,\! }[/math] represents the mean of the natural logarithms of the times-to-failure, while [math]\displaystyle{ {{\sigma' }}\,\! }[/math] represents the standard deviation of these data point logarithms. Specifically, the returned [math]\displaystyle{ {{\sigma' }}\,\! }[/math] is the square root of the variance of the natural logarithms of the data points. Even though the application denotes these values as mean and standard deviation, the user is reminded that these are given as the parameters of the distribution, and are thus the mean and standard deviation of the natural logarithms of the data. The mean value of the times-to-failure, not used as a parameter, as well as the standard deviation can be obtained through the QCP or the Function Wizard.

Lognormal Distribution Examples

Complete Data Example

Determine the lognormal parameter estimates for the data given in the following table.

Non-Grouped Times-to-Failure Data
Data point index	State F or S	State End Time
1	F	2
2	F	5
3	F	11
4	F	23
5	F	29
6	F	37
7	F	43
8	F	59

Solution

Using Weibull++, the computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 2.83 \\ & {\hat{\sigma '}}= & 1.10 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ X\,\! }[/math]

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 2.83 \\ & {{{\hat{\sigma' }}}}= & 1.24 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ Y:\,\! }[/math]

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 2.83 \\ & {{{\hat{\sigma' }}}}= & 1.36 \end{align}\,\! }[/math]

Complete Data RRX Example

From Kececioglu [20, p. 347]. 15 identical units were tested to failure and following is a table of their failure times:

Times-to-Failure Data [math]\displaystyle{ \begin{matrix} \text{Data Point Index} & \text{Failure Times (Hr)} \\ \text{1} & \text{62}\text{.5} \\ \text{2} & \text{91}\text{.9} \\ \text{3} & \text{100}\text{.3} \\ \text{4} & \text{117}\text{.4} \\ \text{5} & \text{141}\text{.1} \\ \text{6} & \text{146}\text{.8} \\ \text{7} & \text{172}\text{.7} \\ \text{8} & \text{192}\text{.5} \\ \text{9} & \text{201}\text{.6} \\ \text{10} & \text{235}\text{.8} \\ \text{11} & \text{249}\text{.2} \\ \text{12} & \text{297}\text{.5} \\ \text{13} & \text{318}\text{.3} \\ \text{14} & \text{410}\text{.6} \\ \text{15} & \text{550}\text{.5} \\ \end{matrix}\,\! }[/math]

Solution

Published results (using probability plotting):

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=5.22575 \\ {{\widehat{\sigma' }}}=0.62048. \\ \end{matrix}\,\! }[/math]

Weibull++ computed parameters for rank regression on X are:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=5.2303 \\ {{\widehat{\sigma'}}}=0.6283. \\ \end{matrix}\,\! }[/math]

The small differences are due to the precision errors when fitting a line manually, whereas in Weibull++ the line was fitted mathematically.

Complete Data Unbiased MLE Example

From Kececioglu [19, p. 406]. 9 identical units are tested continuously to failure and failure times were recorded at 30.4, 36.7, 53.3, 58.5, 74.0, 99.3, 114.3, 140.1 and 257.9 hours.

Solution

The results published were obtained by using the unbiased model. Published Results (using MLE):

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=4.3553 \\ {{\widehat{\sigma' }}}=0.67677 \\ \end{matrix}\,\! }[/math]

This same data set can be entered into Weibull++ by creating a data sheet capable of handling non-grouped time-to-failure data. Since the results shown above are unbiased, the Use Unbiased Std on Normal Data option in the User Setup must be selected in order to duplicate these results. Weibull++ computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=4.3553 \\ {{\widehat{\sigma' }}}=0.6768 \\ \end{matrix}\,\! }[/math]

Suspension Data Example

From Nelson [30, p. 324]. 96 locomotive controls were tested, 37 failed and 59 were suspended after running for 135,000 miles. The table below shows the failure and suspension times.

Nelson's Locomotive Data
	Number in State	F or S	Time
1	1	F	22.5
2	1	F	37.5
3	1	F	46
4	1	F	48.5
5	1	F	51.5
6	1	F	53
7	1	F	54.5
8	1	F	57.5
9	1	F	66.5
10	1	F	68
11	1	F	69.5
12	1	F	76.5
13	1	F	77
14	1	F	78.5
15	1	F	80
16	1	F	81.5
17	1	F	82
18	1	F	83
19	1	F	84
20	1	F	91.5
21	1	F	93.5
22	1	F	102.5
23	1	F	107
24	1	F	108.5
25	1	F	112.5
26	1	F	113.5
27	1	F	116
28	1	F	117
29	1	F	118.5
30	1	F	119
31	1	F	120
32	1	F	122.5
33	1	F	123
34	1	F	127.5
35	1	F	131
36	1	F	132.5
37	1	F	134
38	59	S	135

Solution

The distribution used in the publication was the base-10 lognormal. Published results (using MLE):

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=2.2223 \\ {{\widehat{\sigma' }}}=0.3064 \\ \end{matrix}\,\! }[/math]

Published 95% confidence limits on the parameters:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=\left\{ 2.1336,2.3109 \right\} \\ {{\widehat{\sigma'}}}=\left\{ 0.2365,0.3970 \right\} \\ \end{matrix}\,\! }[/math]

Published variance/covariance matrix:

[math]\displaystyle{ \left[ \begin{matrix} \widehat{Var}\left( {{{\hat{\mu }}}^{\prime }} \right)=0.0020 & {} & \widehat{Cov}({{{\hat{\mu }}}^{\prime }},{{{\hat{\sigma' }}}})=0.001 \\ {} & {} & {} \\ \widehat{Cov}({{{\hat{\mu }}}^{\prime }},{{{\hat{\sigma' }}}})=0.001 & {} & \widehat{Var}\left( {{{\hat{\sigma '}}}} \right)=0.0016 \\ \end{matrix} \right]\,\! }[/math]

To replicate the published results (since Weibull++ uses a lognormal to the base [math]\displaystyle{ e\,\! }[/math] ), take the base-10 logarithm of the data and estimate the parameters using the normal distribution and MLE.

• Weibull++ computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=2.2223 \\ {{\widehat{\sigma' }}}=0.3064 \\ \end{matrix}\,\! }[/math]

• Weibull++ computed 95% confidence limits on the parameters:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=\left\{ 2.1364,2.3081 \right\} \\ {{\widehat{\sigma'}}}=\left\{ 0.2395,0.3920 \right\} \\ \end{matrix}\,\! }[/math]

• Weibull++ computed/variance covariance matrix:

[math]\displaystyle{ \left[ \begin{matrix} \widehat{Var}\left( {{{\hat{\mu }}}^{\prime }} \right)=0.0019 & {} & \widehat{Cov}({{{\hat{\mu }}}^{\prime }},{{{\hat{\sigma' }}}})=0.0009 \\ {} & {} & {} \\ \widehat{Cov}({\mu }',{{{\hat{\sigma' }}}})=0.0009 & {} & \widehat{Var}\left( {{{\hat{\sigma' }}}} \right)=0.0015 \\ \end{matrix} \right]\,\! }[/math]

Interval Data Example

Determine the lognormal parameter estimates for the data given in the table below.

Non-Grouped Data Times-to-Failure with Intervals
Data point index	Last Inspected	State End Time
1	30	32
2	32	35
3	35	37
4	37	40
5	42	42
6	45	45
7	50	50
8	55	55

Solution

This is a sequence of interval times-to-failure where the intervals vary substantially in length. Using Weibull++, the computed parameters for maximum likelihood are calculated to be:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 3.64 \\ & {{{\hat{\sigma' }}}}= & 0.18 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ X\ \,\! }[/math]:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 3.64 \\ & {{{\hat{\sigma' }}}}= & 0.17 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ Y\ \,\! }[/math]:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 3.64 \\ & {{{\hat{\sigma' }}}}= & 0.21 \end{align}\,\! }[/math]

Example 7:

The lognormal distribution is commonly used to model the lives of units whose failure modes are of a fatigue-stress nature. Since this includes most, if not all, mechanical systems, the lognormal distribution can have widespread application. Consequently, the lognormal distribution is a good companion to the Weibull distribution when attempting to model these types of units. As may be surmised by the name, the lognormal distribution has certain similarities to the normal distribution. A random variable is lognormally distributed if the logarithm of the random variable is normally distributed. Because of this, there are many mathematical similarities between the two distributions. For example, the mathematical reasoning for the construction of the probability plotting scales and the bias of parameter estimators is very similar for these two distributions.

Lognormal Probability Density Function

The lognormal distribution is a 2-parameter distribution with parameters [math]\displaystyle{ {\mu }'\,\! }[/math] and [math]\displaystyle{ \sigma'\,\! }[/math]. The pdf for this distribution is given by:

[math]\displaystyle{ f({t}')=\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{t}^{\prime }}-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}\,\! }[/math]

where:

[math]\displaystyle{ {t}'=\ln (t)\,\! }[/math]. [math]\displaystyle{ t\,\! }[/math] values are the times-to-failure

[math]\displaystyle{ \mu'\,\! }[/math] = mean of the natural logarithms of the times-to-failure

[math]\displaystyle{ \sigma'\,\! }[/math] = standard deviation of the natural logarithms of the times-to-failure

The lognormal pdf can be obtained, realizing that for equal probabilities under the normal and lognormal pdfs, incremental areas should also be equal, or:

[math]\displaystyle{ \begin{align} f(t)dt=f({t}')d{t}' \end{align}\,\! }[/math]

Taking the derivative of the relationship between [math]\displaystyle{ {t}'\,\! }[/math] and [math]\displaystyle{ {t}\,\! }[/math] yields:

[math]\displaystyle{ d{t}'=\frac{dt}{t}\,\! }[/math]

Substitution yields:

[math]\displaystyle{ \begin{align} f(t)= & \frac{f({t}')}{t} \\ f(t)= & \frac{1}{t\cdot {{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{\text{ln}(t)-{\mu }'}{{{\sigma' }}} \right)}^{2}}}} \end{align}\,\! }[/math]

where:

[math]\displaystyle{ f(t)\ge 0,t\gt 0,-\infty \lt {\mu }'\lt \infty ,{{\sigma' }}\gt 0\,\! }[/math]

Lognormal Distribution Functions

The Mean or MTTF

The mean of the lognormal distribution, [math]\displaystyle{ \mu \,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ \mu ={{e}^{{\mu }'+\tfrac{1}{2}\sigma'^{2}}}\,\! }[/math]

The mean of the natural logarithms of the times-to-failure, [math]\displaystyle{ \mu'\,\! }[/math], in terms of [math]\displaystyle{ \bar{T}\,\! }[/math] and [math]\displaystyle{ {{\sigma}}\,\! }[/math] is given by:

[math]\displaystyle{ {\mu }'=\ln \left( {\bar{T}} \right)-\frac{1}{2}\ln \left( \frac{\sigma^{2}}{{{{\bar{T}}}^{2}}}+1 \right)\,\! }[/math]

The Median

The median of the lognormal distribution, [math]\displaystyle{ \breve{T}\,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ \breve{T}={{e}^{{{\mu}'}}}\,\! }[/math]

The Mode

The mode of the lognormal distribution, [math]\displaystyle{ \tilde{T}\,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ \tilde{T}={{e}^{{\mu }'-\sigma'^{2}}}\,\! }[/math]

The Standard Deviation

The standard deviation of the lognormal distribution, [math]\displaystyle{ {\sigma }_{T}\,\! }[/math], is discussed in Kececioglu [19]:

[math]\displaystyle{ {\sigma}_{T} =\sqrt{\left( {{e}^{2\mu '+\sigma {{'}^{2}}}} \right)\left( {{e}^{\sigma {{'}^{2}}}}-1 \right)}\,\! }[/math]

The standard deviation of the natural logarithms of the times-to-failure, [math]\displaystyle{ {\sigma}'\,\! }[/math], in terms of [math]\displaystyle{ \bar{T}\,\! }[/math] and [math]\displaystyle{ {\sigma}\,\! }[/math] is given by:

[math]\displaystyle{ \sigma '=\sqrt{\ln \left( \frac{{\sigma}_{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)}\,\! }[/math]

The Lognormal Reliability Function

The reliability for a mission of time [math]\displaystyle{ t\,\! }[/math], starting at age 0, for the lognormal distribution is determined by:

[math]\displaystyle{ R(t)=\int_{t}^{\infty }f(x)dx\,\! }[/math]

or:

[math]\displaystyle{ {{R}({t})}=\int_{\text{ln}(t)}^{\infty }\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx\,\! }[/math]

As with the normal distribution, there is no closed-form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability we will not discuss manual solution methods. For interested readers, full explanations can be found in the references.

The Lognormal Conditional Reliability Function

The lognormal conditional reliability function is given by:

[math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)}=\frac{\int_{\text{ln}(T+t)}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}ds}{\int_{\text{ln}(T)}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx}\,\! }[/math]

Once again, the use of standard normal tables is necessary to solve this equation, as no closed-form solution exists.

The Lognormal Reliable Life Function

As there is no closed-form solution for the lognormal reliability equation, no closed-form solution exists for the lognormal reliable life either. In order to determine this value, one must solve the following equation for [math]\displaystyle{ t\,\! }[/math]:

[math]\displaystyle{ {{R}_{t}}=\int_{\text{ln}(t)}^{\infty }\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx\,\! }[/math]

The Lognormal Failure Rate Function

The lognormal failure rate is given by:

[math]\displaystyle{ \lambda (t)=\frac{f(t)}{R(t)}=\frac{\tfrac{1}{t\cdot {{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{{t}'-{\mu }'}{{{\sigma' }}})}^{2}}}}}{\int_{{{t}'}}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{x-{\mu }'}{{{\sigma' }}})}^{2}}}}dx}\,\! }[/math]

As with the reliability equations, standard normal tables will be required to solve for this function.

Characteristics of the Lognormal Distribution

• The lognormal distribution is a distribution skewed to the right.
• The pdf starts at zero, increases to its mode, and decreases thereafter.
• The degree of skewness increases as [math]\displaystyle{ {{\sigma'}}\,\! }[/math] increases, for a given [math]\displaystyle{ \mu'\,\! }[/math]

• For the same [math]\displaystyle{ {{\sigma'}}\,\! }[/math], the pdf 's skewness increases as [math]\displaystyle{ {\mu }'\,\! }[/math] increases.
• For [math]\displaystyle{ {{\sigma' }}\,\! }[/math] values significantly greater than 1, the pdf rises very sharply in the beginning, (i.e., for very small values of [math]\displaystyle{ T\,\! }[/math] near zero), and essentially follows the ordinate axis, peaks out early, and then decreases sharply like an exponential pdf or a Weibull pdf with [math]\displaystyle{ 0\lt \beta \lt 1\,\! }[/math].
• The parameter, [math]\displaystyle{ {\mu }'\,\! }[/math], in terms of the logarithm of the [math]\displaystyle{ {T}'s\,\! }[/math] is also the scale parameter, and not the location parameter as in the case of the normal pdf.
• The parameter [math]\displaystyle{ {{\sigma'}}\,\! }[/math], or the standard deviation of the [math]\displaystyle{ {T}'s\,\! }[/math] in terms of their logarithm or of their [math]\displaystyle{ {T}'\,\! }[/math], is also the shape parameter and not the scale parameter, as in the normal pdf, and assumes only positive values.

Lognormal Distribution Parameters in ReliaSoft's Software

In ReliaSoft's software, the parameters returned for the lognormal distribution are always logarithmic. That is: the parameter [math]\displaystyle{ {\mu }'\,\! }[/math] represents the mean of the natural logarithms of the times-to-failure, while [math]\displaystyle{ {{\sigma' }}\,\! }[/math] represents the standard deviation of these data point logarithms. Specifically, the returned [math]\displaystyle{ {{\sigma' }}\,\! }[/math] is the square root of the variance of the natural logarithms of the data points. Even though the application denotes these values as mean and standard deviation, the user is reminded that these are given as the parameters of the distribution, and are thus the mean and standard deviation of the natural logarithms of the data. The mean value of the times-to-failure, not used as a parameter, as well as the standard deviation can be obtained through the QCP or the Function Wizard.

Lognormal Distribution Examples

Complete Data Example

Determine the lognormal parameter estimates for the data given in the following table.

Non-Grouped Times-to-Failure Data
Data point index	State F or S	State End Time
1	F	2
2	F	5
3	F	11
4	F	23
5	F	29
6	F	37
7	F	43
8	F	59

Solution

Using Weibull++, the computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 2.83 \\ & {\hat{\sigma '}}= & 1.10 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ X\,\! }[/math]

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 2.83 \\ & {{{\hat{\sigma' }}}}= & 1.24 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ Y:\,\! }[/math]

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 2.83 \\ & {{{\hat{\sigma' }}}}= & 1.36 \end{align}\,\! }[/math]

Complete Data RRX Example

From Kececioglu [20, p. 347]. 15 identical units were tested to failure and following is a table of their failure times:

Times-to-Failure Data [math]\displaystyle{ \begin{matrix} \text{Data Point Index} & \text{Failure Times (Hr)} \\ \text{1} & \text{62}\text{.5} \\ \text{2} & \text{91}\text{.9} \\ \text{3} & \text{100}\text{.3} \\ \text{4} & \text{117}\text{.4} \\ \text{5} & \text{141}\text{.1} \\ \text{6} & \text{146}\text{.8} \\ \text{7} & \text{172}\text{.7} \\ \text{8} & \text{192}\text{.5} \\ \text{9} & \text{201}\text{.6} \\ \text{10} & \text{235}\text{.8} \\ \text{11} & \text{249}\text{.2} \\ \text{12} & \text{297}\text{.5} \\ \text{13} & \text{318}\text{.3} \\ \text{14} & \text{410}\text{.6} \\ \text{15} & \text{550}\text{.5} \\ \end{matrix}\,\! }[/math]

Solution

Published results (using probability plotting):

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=5.22575 \\ {{\widehat{\sigma' }}}=0.62048. \\ \end{matrix}\,\! }[/math]

Weibull++ computed parameters for rank regression on X are:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=5.2303 \\ {{\widehat{\sigma'}}}=0.6283. \\ \end{matrix}\,\! }[/math]

The small differences are due to the precision errors when fitting a line manually, whereas in Weibull++ the line was fitted mathematically.

Complete Data Unbiased MLE Example

From Kececioglu [19, p. 406]. 9 identical units are tested continuously to failure and failure times were recorded at 30.4, 36.7, 53.3, 58.5, 74.0, 99.3, 114.3, 140.1 and 257.9 hours.

Solution

The results published were obtained by using the unbiased model. Published Results (using MLE):

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=4.3553 \\ {{\widehat{\sigma' }}}=0.67677 \\ \end{matrix}\,\! }[/math]

This same data set can be entered into Weibull++ by creating a data sheet capable of handling non-grouped time-to-failure data. Since the results shown above are unbiased, the Use Unbiased Std on Normal Data option in the User Setup must be selected in order to duplicate these results. Weibull++ computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=4.3553 \\ {{\widehat{\sigma' }}}=0.6768 \\ \end{matrix}\,\! }[/math]

Suspension Data Example

From Nelson [30, p. 324]. 96 locomotive controls were tested, 37 failed and 59 were suspended after running for 135,000 miles. The table below shows the failure and suspension times.

Nelson's Locomotive Data
	Number in State	F or S	Time
1	1	F	22.5
2	1	F	37.5
3	1	F	46
4	1	F	48.5
5	1	F	51.5
6	1	F	53
7	1	F	54.5
8	1	F	57.5
9	1	F	66.5
10	1	F	68
11	1	F	69.5
12	1	F	76.5
13	1	F	77
14	1	F	78.5
15	1	F	80
16	1	F	81.5
17	1	F	82
18	1	F	83
19	1	F	84
20	1	F	91.5
21	1	F	93.5
22	1	F	102.5
23	1	F	107
24	1	F	108.5
25	1	F	112.5
26	1	F	113.5
27	1	F	116
28	1	F	117
29	1	F	118.5
30	1	F	119
31	1	F	120
32	1	F	122.5
33	1	F	123
34	1	F	127.5
35	1	F	131
36	1	F	132.5
37	1	F	134
38	59	S	135

Solution

The distribution used in the publication was the base-10 lognormal. Published results (using MLE):

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=2.2223 \\ {{\widehat{\sigma' }}}=0.3064 \\ \end{matrix}\,\! }[/math]

Published 95% confidence limits on the parameters:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=\left\{ 2.1336,2.3109 \right\} \\ {{\widehat{\sigma'}}}=\left\{ 0.2365,0.3970 \right\} \\ \end{matrix}\,\! }[/math]

Published variance/covariance matrix:

[math]\displaystyle{ \left[ \begin{matrix} \widehat{Var}\left( {{{\hat{\mu }}}^{\prime }} \right)=0.0020 & {} & \widehat{Cov}({{{\hat{\mu }}}^{\prime }},{{{\hat{\sigma' }}}})=0.001 \\ {} & {} & {} \\ \widehat{Cov}({{{\hat{\mu }}}^{\prime }},{{{\hat{\sigma' }}}})=0.001 & {} & \widehat{Var}\left( {{{\hat{\sigma '}}}} \right)=0.0016 \\ \end{matrix} \right]\,\! }[/math]

To replicate the published results (since Weibull++ uses a lognormal to the base [math]\displaystyle{ e\,\! }[/math] ), take the base-10 logarithm of the data and estimate the parameters using the normal distribution and MLE.

• Weibull++ computed parameters for maximum likelihood are:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=2.2223 \\ {{\widehat{\sigma' }}}=0.3064 \\ \end{matrix}\,\! }[/math]

• Weibull++ computed 95% confidence limits on the parameters:

[math]\displaystyle{ \begin{matrix} {{\widehat{\mu }}^{\prime }}=\left\{ 2.1364,2.3081 \right\} \\ {{\widehat{\sigma'}}}=\left\{ 0.2395,0.3920 \right\} \\ \end{matrix}\,\! }[/math]

• Weibull++ computed/variance covariance matrix:

[math]\displaystyle{ \left[ \begin{matrix} \widehat{Var}\left( {{{\hat{\mu }}}^{\prime }} \right)=0.0019 & {} & \widehat{Cov}({{{\hat{\mu }}}^{\prime }},{{{\hat{\sigma' }}}})=0.0009 \\ {} & {} & {} \\ \widehat{Cov}({\mu }',{{{\hat{\sigma' }}}})=0.0009 & {} & \widehat{Var}\left( {{{\hat{\sigma' }}}} \right)=0.0015 \\ \end{matrix} \right]\,\! }[/math]

Interval Data Example

Determine the lognormal parameter estimates for the data given in the table below.

Non-Grouped Data Times-to-Failure with Intervals
Data point index	Last Inspected	State End Time
1	30	32
2	32	35
3	35	37
4	37	40
5	42	42
6	45	45
7	50	50
8	55	55

Solution

This is a sequence of interval times-to-failure where the intervals vary substantially in length. Using Weibull++, the computed parameters for maximum likelihood are calculated to be:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 3.64 \\ & {{{\hat{\sigma' }}}}= & 0.18 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ X\ \,\! }[/math]:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 3.64 \\ & {{{\hat{\sigma' }}}}= & 0.17 \end{align}\,\! }[/math]

For rank regression on [math]\displaystyle{ Y\ \,\! }[/math]:

[math]\displaystyle{ \begin{align} & {{{\hat{\mu }}}^{\prime }}= & 3.64 \\ & {{{\hat{\sigma' }}}}= & 0.21 \end{align}\,\! }[/math]