Template:Normal distribution rank regression on Y

Rank Regression on Y

Performing rank regression on Y requires that a straight line be fitted to a set of data points such that the sum of the squares of the vertical deviations from the points to the line is minimized.

The least squares parameter estimation method (regression analysis) was discussed in ChapterChapParameter Estimation and the following equations for regression on Y were derived:

[math]\displaystyle{ \begin{align}\hat{a}= & \bar{b}-\hat{b}\bar{x} \\ =& \frac{\sum_{i=1}^N y_{i}}{N}-\hat{b}\frac{\sum_{i=1}^{N}x_{i}}{N}\\ \end{align} }[/math]

and:

[math]\displaystyle{ \hat{b}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}{{y}_{i}}-\tfrac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}}{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,x_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}} \right)}^{2}}}{N}} }[/math]

In the case of the normal distribution, the equations for [math]\displaystyle{ {{y}_{i}} }[/math] and [math]\displaystyle{ {{x}_{i}} }[/math] are:

[math]\displaystyle{ {{y}_{i}}={{\Phi }^{-1}}\left[ F({{T}_{i}}) \right] }[/math]

and:

[math]\displaystyle{ {{x}_{i}}={{T}_{i}} }[/math]

where the values for [math]\displaystyle{ F({{T}_{i}}) }[/math] are estimated from the median ranks. Once [math]\displaystyle{ \widehat{a} }[/math] and [math]\displaystyle{ \widehat{b} }[/math] are obtained, [math]\displaystyle{ \widehat{\sigma } }[/math] and [math]\displaystyle{ \widehat{\mu } }[/math] can easily be obtained from Eqns. (an) and (bn).

The Correlation Coefficient

The estimator of the sample correlation coefficient, [math]\displaystyle{ \hat{\rho } }[/math] , is given by:

[math]\displaystyle{ \hat{\rho }=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,({{x}_{i}}-\overline{x})({{y}_{i}}-\overline{y})}{\sqrt{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{({{x}_{i}}-\overline{x})}^{2}}\cdot \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{({{y}_{i}}-\overline{y})}^{2}}}} }[/math]

Example 2

Fourteen units were reliability tested and the following life test data were obtained:

Table 8.1 -The test data for Example 2
Data point index	Time-to-failure
1	5
2	10
3	15
4	20
5	25
6	30
7	35
8	40
9	50
10	60
11	70
12	80
13	90
14	100

Assuming the data follow a normal distribution, estimate the parameters and determine the correlation coefficient, [math]\displaystyle{ \rho }[/math] , using rank regression on Y.

Solution to Example 2

Construct a table like the one shown next.

[math]\displaystyle{ \overset{{}}{\mathop{\text{Table 8}\text{.2 - Least Squares Analysis}}}\, }[/math] [math]\displaystyle{ \begin{matrix} \text{N} & \text{T}_{i} & \text{F(T}_{i}\text{)} & \text{y}_{i} & \text{T}_{i}^{2} & \text{y}_{i}^{2} & \text{T}_{i}\text{ y}_{i} \\ \text{1} & \text{5} & \text{0}\text{.0483} & \text{-1}\text{.6619} & \text{25} & \text{2}\text{.7619} & \text{-8}\text{.3095} \\ \text{2} & \text{10} & \text{0}\text{.1170} & \text{-1}\text{.1901} & \text{100} & \text{1}\text{.4163} & \text{-11}\text{.9010} \\ \text{3} & \text{15} & \text{0}\text{.1865} & \text{-0}\text{.8908} & \text{225} & \text{0}\text{.7935} & \text{-13}\text{.3620} \\ \text{4} & \text{20} & \text{0}\text{.2561} & \text{-0}\text{.6552} & \text{400} & \text{0}\text{.4292} & \text{-13}\text{.1030} \\ \text{5} & \text{25} & \text{0}\text{.3258} & \text{-0}\text{.4512} & \text{625} & \text{0}\text{.2036} & \text{-11}\text{.2800} \\ \text{6} & \text{30} & \text{0}\text{.3954} & \text{-0}\text{.2647} & \text{900} & \text{0}\text{.0701} & \text{-7}\text{.9422} \\ \text{7} & \text{35} & \text{0}\text{.4651} & \text{-0}\text{.0873} & \text{1225} & \text{0}\text{.0076} & \text{-3}\text{.0542} \\ \text{8} & \text{40} & \text{0}\text{.5349} & \text{0}\text{.0873} & \text{1600} & \text{0}\text{.0076} & \text{3}\text{.4905} \\ \text{9} & \text{50} & \text{0}\text{.6046} & \text{0}\text{.2647} & \text{2500} & \text{0}\text{.0701} & \text{13}\text{.2370} \\ \text{10} & \text{60} & \text{0}\text{.6742} & \text{0}\text{.4512} & \text{3600} & \text{0}\text{.2036} & \text{27}\text{.0720} \\ \text{11} & \text{70} & \text{0}\text{.7439} & \text{0}\text{.6552} & \text{4900} & \text{0}\text{.4292} & \text{45}\text{.8605} \\ \text{12} & \text{80} & \text{0}\text{.8135} & \text{0}\text{.8908} & \text{6400} & \text{0}\text{.7935} & \text{71}\text{.2640} \\ \text{13} & \text{90} & \text{0}\text{.8830} & \text{1}\text{.1901} & \text{8100} & \text{1}\text{.4163} & \text{107}\text{.1090} \\ \text{14} & \text{100} & \text{0}\text{.9517} & \text{1}\text{.6619} & \text{10000} & \text{2}\text{.7619} & \text{166}\text{.1900} \\ \mathop{}_{}^{} & \text{630} & {} & \text{0} & \text{40600} & \text{11}\text{.3646} & \text{365}\text{.2711} \\ \end{matrix} }[/math]

• The median rank values ( [math]\displaystyle{ F({{T}_{i}}) }[/math] ) can be found in rank tables, available in many statistical texts, or they can be estimated by using the Quick Statistical Reference in Weibull++.

• The [math]\displaystyle{ {{y}_{i}} }[/math] values were obtained from standardized normal distribution's area tables by entering for [math]\displaystyle{ F(z) }[/math] and getting the corresponding [math]\displaystyle{ z }[/math] value ( [math]\displaystyle{ {{y}_{i}} }[/math] ). As with the median rank values, these standard normal values can be obtained with the Quick Statistical Reference.

Given the values in Table 8.2, calculate [math]\displaystyle{ \widehat{a} }[/math] and [math]\displaystyle{ \widehat{b} }[/math] using Eqns. (aan) and (bbn):

[math]\displaystyle{ \begin{align} & \widehat{b}= & \frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}}{{y}_{i}}-(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}})(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}})/14}{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,T_{i}^{2}-{{(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}})}^{2}}/14} \\ & & \\ & \widehat{b}= & \frac{365.2711-(630)(0)/14}{40,600-{{(630)}^{2}}/14}=0.02982 \end{align} }[/math]

and:

[math]\displaystyle{ \widehat{a}=\overline{y}-\widehat{b}\overline{T}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\widehat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{T}_{i}}}{N} }[/math]

or:

[math]\displaystyle{ \widehat{a}=\frac{0}{14}-(0.02982)\frac{630}{14}=-1.3419 }[/math]

Therefore, from Eqn. (bn):

[math]\displaystyle{ \widehat{\sigma}=\frac{1}{\hat{b}}=\frac{1}{0.02982}=33.5367 }[/math]

and from Eqn. (an):

[math]\displaystyle{ \widehat{\mu }=-\widehat{a}\cdot \widehat{\sigma }=-(-1.3419)\cdot 33.5367\simeq 45 }[/math]

or [math]\displaystyle{ \widehat{\mu }=45 }[/math] hours [math]\displaystyle{ . }[/math]

The correlation coefficient can be estimated using Eqn. (RHOn):

[math]\displaystyle{ \widehat{\rho }=0.979 }[/math]

The preceding example can be repeated using Weibull++ .

• Create a new folio for Times-to-Failure data, and enter the data given in Table 8.1.

• Choose Normal from the Distributions list.

• Go to the Analysis page and select Rank Regression on Y (RRY).

• Click the Calculate icon located on the Main page.

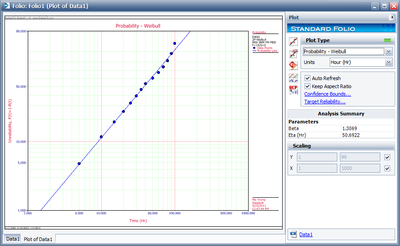
The probability plot is shown next.