Multivariable Relationships: General Log-Linear and Proportional Hazards

Multivariable Relationships: General Log-Linear and Proportional Hazards

Introduction

So far in this reference the life-stress relationships presented have been either single stress relationships (Chapters 6, 7, and 8) or two stress relationships (Chapters 9 and 10). In most practical applications, however, life is a function of more than one or two variables (stress types). In addition, there are many applications where the life of a product as a function of stress and of some engineering variable other than stress is sought. In this chapter, the general log-linear relationship and the proportional hazards model are presented for the analysis of such cases where more than two accelerated stresses (or variables) need to be considered.

General Log-Linear Relationship

When a test involves multiple accelerating stresses or requires the inclusion of an engineering variable, a general multivariable relationship is needed. Such a relationship is the general log-linear relationship, which describes a life characteristic as a function of a vector of [math]\displaystyle{ n }[/math] stresses, or [math]\displaystyle{ \underline{X}=({{X}_{1}},{{X}_{2}}...{{X}_{n}}). }[/math] ALTA PRO includes this relationship and allows up to eight stresses. Mathematically the relationship is given by:

[math]\displaystyle{ L(\underline{X})={{e}^{{{\alpha }_{0}}+\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}}}} }[/math]

where:

• [math]\displaystyle{ {{\alpha }_{0}} }[/math] and [math]\displaystyle{ {{\alpha }_{j}} }[/math] are model parameters.

• [math]\displaystyle{ X }[/math] is a vector of [math]\displaystyle{ n }[/math] stresses.

This relationship can be further modified through the use of transformations and can be reduced to the relationships discussed previously, if so desired. As an example, consider a single stress application of this relationship and an inverse transformation on [math]\displaystyle{ X, }[/math] such that [math]\displaystyle{ V=1/X }[/math] or:

[math]\displaystyle{ \begin{align} & L(V)= & {{e}^{{{\alpha }_{0}}+\tfrac{{{\alpha }_{1}}}{V}}} \\ & = & {{e}^{{{\alpha }_{0}}}}{{e}^{\tfrac{{{\alpha }_{1}}}{V}}} \end{align} }[/math]

It can be easily seen that the generalized log-linear relationship with a single stress and an inverse transformation, Eqn. (argll), has been reduced to the Arrhenius relationship discussed in Chapter 6, where:

[math]\displaystyle{ \begin{align} & C= & {{e}^{{{\alpha }_{0}}}} \\ & B= & {{\alpha }_{1}} \end{align} }[/math]

or:

[math]\displaystyle{ L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]

Similarly, when one chooses to apply a logarithmic transformation on [math]\displaystyle{ X }[/math] such that [math]\displaystyle{ V=\ln (X) }[/math] , the relationship would reduce to the inverse power relation discussed in Chapter 8. Furthermore, if more than one stress is present, one could choose to apply a different transformation to each stress to create combination relationships similar to the ones discussed in Chapters 9 and 10. ALTA PRO has three built-in transformation options, namely:

None	X=V	Exponential LSR
Reciprocal	[math]\displaystyle{ V=1/X }[/math]	Arrhenius LSR
Logarithmic	[math]\displaystyle{ V=\ln (X) }[/math]	Power LSR

The power of the relationship and this formulation becomes evident once one realizes that 6,651 unique life-stress relationships are possible (when allowing a maximum of eight stresses). When combined with the life distributions available in ALTA PRO, almost 20,000 models can be created.

Using the GLL Model

Like the previous relationships, the general log-linear relationship can be combined with any of the available life distributions by expressing a life characteristic from that distribution with the GLL relationship. A brief overview of the GLL-distribution models available in ALTA PRO is presented next.

GLL Exponential

The GLL-exponential model can be derived by setting [math]\displaystyle{ m=L(\underline{X}) }[/math] in Eqn. (GLL1), yielding the following GLL-exponential [math]\displaystyle{ pdf }[/math] :

[math]\displaystyle{ f(t,\underline{X})={{e}^{-\left( {{\alpha }_{0}}+\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}} \right)}}{{e}^{-\left( {{\alpha }_{0}}+\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}} \right)\cdot t}} }[/math]

The total number of unknowns to solve for in this model is [math]\displaystyle{ n+1 }[/math] (i.e. [math]\displaystyle{ {{a}_{0}},{{a}_{1}},...{{a}_{n}}). }[/math]

GLL Weibull

The GLL-Weibull model can be derived by setting [math]\displaystyle{ \eta =L(\underline{X}) }[/math] in Eqn. (GLL1), yielding the following GLL-Weibull [math]\displaystyle{ pdf }[/math] :

[math]\displaystyle{ f(t,\underline{X})=\beta \cdot {{t}^{\beta -1}}{{e}^{-\beta \left( {{\alpha }_{0}}+\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}} \right)}}{{e}^{-{{t}^{\beta }}{{e}^{-\beta \left( {{\alpha }_{0}}+\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}} \right)}}}} }[/math]

The total number of unknowns to solve for in this model is [math]\displaystyle{ n+2 }[/math] (i.e. [math]\displaystyle{ \beta ,{{a}_{0}},{{a}_{1}},...{{a}_{n}}). }[/math]

GLL Lognormal

The GLL-lognormal model can be derived by setting [math]\displaystyle{ \breve{T}=L(\underline{X}) }[/math] in Eqn. (GLL1), yielding the following GLL-lognormal [math]\displaystyle{ pdf }[/math] :

[math]\displaystyle{ f(t,\underline{X})=\frac{1}{t\text{ }{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-{{\alpha }_{0}}-\underset{j=1}{\overset{n}{\mathop{\sum }}}\,{{\alpha }_{j}}{{X}_{j}}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}} }[/math]

The total number of unknowns to solve for in this model is [math]\displaystyle{ n+2 }[/math] (i.e. [math]\displaystyle{ {{\sigma }_{{{T}'}}},{{a}_{0}},{{a}_{1}},...{{a}_{n}}). }[/math]

GLL Likelihood Function

The maximum likelihood estimation method can be used to determine the parameters for the GLL relationship and the selected life distribution. For each distribution, the likelihood function can be derived, and the parameters of model (the distribution parameters and the GLL parameters) can be obtained by maximizing the log-likelihood function. For example, the log-likelihood function for the Weibull distribution is given by:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \beta \cdot T_{i}^{\beta -1}{{e}^{-T_{i}^{\beta }\cdot {{e}^{-\beta \left( {{\alpha }_{0}}+\mathop{}_{j=1}^{n}{{a}_{j}}{{x}_{i,j}} \right)}}}}{{e}^{-\beta \left( {{\alpha }_{0}}+\mathop{}_{j=1}^{n}{{a}_{j}}{{x}_{i,j}} \right)}} \right] \\ & & -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( T_{i}^{\prime } \right)}^{\beta }}{{e}^{-\beta \left( {{\alpha }_{0}}+\mathop{}_{j=1}^{n}{{a}_{j}}{{x}_{i,j}} \right)}}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & R_{Li}^{\prime \prime }= & {{e}^{-{{\left( T_{Li}^{\prime \prime }{{e}^{{{\alpha }_{0}}+\underset{j=1}{\mathop{\overset{n}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}}} \right)}^{\beta }}}} \\ & R_{Ri}^{\prime \prime }= & {{e}^{-{{\left( T_{Ri}^{\prime \prime }{{e}^{{{\alpha }_{0}}+\underset{j=1}{\mathop{\overset{n}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}}} \right)}^{\beta }}}} \end{align} }[/math]

and:

• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ \lambda }[/math] is the failure rate parameter (unknown).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Example

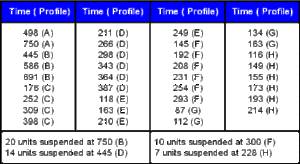
Consider the data summarized in Table 1 and Table 2. These data illustrate a typical three stress type accelerated test.

Table 1: Stress Profile Summary

Table 2: Failure Data

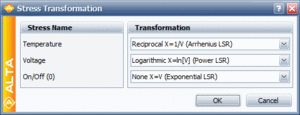
The data of Table 2 is analyzed assuming a Weibull distribution, an Arrhenius life-stress relationship for temperature and an inverse power life-stress relationship for voltage. No transformation is performed on the operation type. The operation type variable is treated as an indicator variable, taking the discrete values of 0 and 1, for on/off and continuous operation, respectively. The following figure, shows the stress types and their transformations as in ALTA.

Eqn. (GLL1) then becomes:

[math]\displaystyle{ \eta ={{e}^{{{\alpha }_{0}}+{{\alpha }_{1}}\tfrac{1}{{{V}_{1}}}+{{\alpha }_{2}}\ln ({{V}_{2}})+{{\alpha }_{3}}{{V}_{3}}}} }[/math]

The resulting relationship after performing these transformations is:

[math]\displaystyle{ \begin{align} & \eta = & {{e}^{{{\alpha }_{0}}}}{{e}^{{{\alpha }_{1}}\tfrac{1}{{{V}_{1}}}}}{{e}^{{{\alpha }_{2}}\ln ({{V}_{2}})}}{{e}^{{{\alpha }_{3}}{{V}_{3}}}} \\ & = & {{e}^{{{\alpha }_{0}}}}{{e}^{{{\alpha }_{1}}\tfrac{1}{{{V}_{1}}}}}V_{2}^{{{\alpha }_{2}}}{{e}^{{{\alpha }_{3}}{{V}_{3}}}} \end{align} }[/math]

Therefore, the parameter [math]\displaystyle{ B }[/math] of the Arrhenius relationship is equal to the log-linear coefficient [math]\displaystyle{ {{\alpha }_{1}} }[/math] , and the parameter [math]\displaystyle{ n }[/math] of the inverse power relationship is equal to ( [math]\displaystyle{ -{{\alpha }_{2}} }[/math] ). Therefore [math]\displaystyle{ \eta }[/math] can also be written as:

[math]\displaystyle{ \eta ={{e}^{{{\alpha }_{0}}}}{{e}^{\tfrac{B}{{{V}_{1}}}}}V_{2}^{n}{{e}^{{{\alpha }_{3}}{{V}_{3}}}} }[/math]

The activation energy of the Arrhenius relationship can be calculated by multiplying B with Boltzmann's constant.
The best fit values for the parameters in this case are:

[math]\displaystyle{ \begin{align} & \beta = & 3.7483;\text{ }{{\alpha }_{0}}=-6.0220;\text{ }{{\alpha }_{1}}=5776.9341 \\ & {{\alpha }_{2}}= & -1.4340;\text{ }{{\alpha }_{3}}=0.6242. \end{align} }[/math]

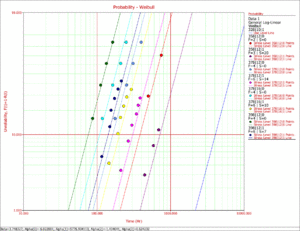
Once the parameters are estimated, further analysis on the data can be performed. First, using ALTA PRO, a Weibull probability plot of the data can be obtained, as shown in Fig. 1.

Weibull probability plot for all covariates.

Several types of information about the model as well as the data can be obtained from a probability plot. For example, the choice of an underlying distribution and the assumption of a common slope (shape parameter) can be examined. In this example, the linearity of the data supports the use of the Weibull distribution. In addition, the data appear parallel on this plot, therefore reinforcing the assumption of a common beta. Further statistical analysis can and should be performed for these purposes as well. The Life vs. Stress plot is a very common plot for the analysis of accelerated data. Life vs. Stress plots can be very useful in assessing the effect of each stress on a product's failure. In this case, since the life is a function of three stresses, three different plots can be created. Such plots are created by holding two of the stresses constant at the desired use level, and varying the remaining one. The use stress levels for this example are 328K for temperature and 10V for voltage. For the operation type, a decision has to be made by the engineers as to whether they implement on/off or continuous operation. Figs. 2 and 3 display the effects of temperature and voltage on the life of the product.

Effects of temperature on life.

Effects of voltage on life.

The effects of the two different operation types on life can be observed in Fig. 4. It can be seen that the on/off cycling has a greater effect on the life of the product in terms of accelerating failure than the continuous operation. In other words, a higher reliability can be achieved by running the product continuously.

Effect of operation type on life.

Proportional Hazards Model

Introduced by D. R. Cox, the Proportional Hazards (PH) model was developed in order to estimate the effects of different covariates influencing the times-to-failure of a system. The model has been widely used in the biomedical field [22], and recently there has been an increasing interest in its application in reliability engineering. In its original form, the model is non-parametric, i.e. no assumptions are made about the nature or shape of the underlying failure distribution. In this reference, the original non-parametric formulation as well as a parametric form of the model will be considered utilizing a Weibull life distribution. In ALTA PRO, the proportional hazards model is included in its parametric form and can be used to analyze data with up to eight variables. The GLL-Weibull and GLL-exponential models are actually special cases of the proportional hazards model. However, when using the proportional hazards in ALTA, no transformation on the covariates (or stresses) can be performed.

Non-Parametric Model Formulation

According to the PH model, the failure rate of a system is affected not only by its operation time, but also by the covariates under which it operates. For example, a unit may have been tested under a combination of different accelerated stresses such as humidity, temperature, voltage, etc. It is clear then that such factors affect the failure rate of a unit. The instantaneous failure rate (or hazard rate) of a unit is given by:

[math]\displaystyle{ \lambda (t)=\frac{f(t)}{R(t)} }[/math]

where:
• [math]\displaystyle{ f(t) }[/math] is the probability density function.
• [math]\displaystyle{ R(t) }[/math] is the reliability function. Note that for the case of the failure rate of a unit being dependent not only on time but also on other covariates, the above equation must be modified in order to be a function of time and of the covariates. The proportional hazards model assumes that the failure rate (hazard rate) of a unit is the product of:
• an arbitrary and unspecified baseline failure rate, [math]\displaystyle{ {{\lambda }_{0}}(t), }[/math] which is a function of time only.
• a positive function [math]\displaystyle{ g(x,\underline{A}) }[/math] , independent of time, which incorporates the effects of a number of covariates such as humidity, temperature, pressure, voltage, etc.
The failure rate of a unit is then given by:

[math]\displaystyle{ \lambda (t,\underline{X})={{\lambda }_{0}}(t)\cdot g(\underline{X},\underline{A}) }[/math]

where:

[math]\displaystyle{ \underline{X} }[/math] is a row vector consisting of the covariates:

[math]\displaystyle{ \underline{X}=({{x}_{1}},{{x}_{2}},...,{{x}_{m}}) }[/math]

[math]\displaystyle{ \underline{A} }[/math] is a column vector consisting of the unknown parameters (also called regression parameters) of the model:

[math]\displaystyle{ \underline{A}={{({{a}_{1}},{{a}_{2}},...{{a}_{m}})}^{T}} }[/math]

where:

[math]\displaystyle{ \quad \quad m }[/math] = number of stress related variates (time-independent).

It can be assumed that the form of [math]\displaystyle{ g(\underline{X},\underline{A}) }[/math] is known and [math]\displaystyle{ {{\lambda }_{0}}(t) }[/math] is unspecified. Different forms of [math]\displaystyle{ g(\underline{X},\underline{A}) }[/math] can be used.

However, the exponential form is mostly used due to its simplicity and is given by:

[math]\displaystyle{ g(\underline{X},\underline{A})={{e}^{{{\underline{A}}^{T}}{{\underline{X}}^{T}}}}={{e}^{\mathop{}_{j=1}^{m}{{a}_{j}}{{x}_{j}}}} }[/math]

The failure rate can then be written as:

[math]\displaystyle{ \lambda (t,\underline{X})={{\lambda }_{0}}(t)\cdot {{e}^{\mathop{}_{j=1}^{m}{{a}_{j}}{{x}_{j}}}} }[/math]

Parametric Model Formulation

A parametric form of the proportional hazards model can be obtained by assuming an underlying distribution. In ALTA PRO, the Weibull and exponential distributions are available. In this section we will consider the Weibull distribution to formulate the parametric proportional hazards model. In other words, it is assumed that the baseline failure rate in Eqn. (Prop. Failure Rate) is parametric and given by the Weibull distribution. In this case, the baseline failure rate is given by:

[math]\displaystyle{ {{\lambda }_{0}}(t)=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}} }[/math]

The PH failure rate then becomes:

[math]\displaystyle{ \lambda (t,\underline{X})=\frac{\beta }{\eta }{{\left( \frac{t}{\eta } \right)}^{\beta -1}}\cdot {{e}^{\mathop{}_{j=1}^{m}{{a}_{j}}{{x}_{j}}}} }[/math]

It is often more convenient to define an additional covariate, [math]\displaystyle{ {{x}_{0}} }[/math] = 1, in order to allow the Weibull scale parameter raised to the beta (shape parameter) to be included in the vector of regression coefficients. The PH failure rate can then be written as:

[math]\displaystyle{ \lambda (t,\underline{X})=\beta \cdot {{t}^{\beta -1}}\cdot {{e}^{\mathop{}_{j=0}^{m}{{a}_{j}}{{x}_{j}}}} }[/math]

The PH reliability function is given by:

[math]\displaystyle{ \begin{align} & R(t,\underline{X})= & {{e}^{-\mathop{}_{0}^{t}\lambda (u)du}} \\ & = & {{e}^{-\mathop{}_{0}^{t}\lambda (u,\underline{X})du}} \\ & = & {{e}^{-{{t}^{\beta }}\cdot {{e}^{\mathop{}_{j=0}^{m}{{a}_{j}}{{x}_{j}}}}}} \end{align} }[/math]

The [math]\displaystyle{ pdf }[/math] can be obtained by taking the partial derivative of the reliability function given by Eqn. (PH Rel) with respect to time. The PH [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ \begin{align} & f(t,\underline{X})= & \lambda (t,\underline{X})\cdot R(t,\underline{X}) \\ & = & \beta \cdot {{t}^{\beta -1}}{{e}^{\left[ \mathop{}_{j=0}^{m}{{a}_{j}}{{x}_{j}}-{{t}^{\beta }}\cdot {{e}^{\mathop{}_{j=0}^{m}{{a}_{j}}{{x}_{j}}}} \right]}} \end{align} }[/math]

The total number of unknowns to solve for in this model is [math]\displaystyle{ m+2 }[/math] (i.e. [math]\displaystyle{ \beta ,\eta ,{{a}_{0}},{{a}_{1}},...{{a}_{m}}). }[/math]
The maximum likelihood estimation method can be used to determine these parameters. The log-likelihood function for this case is given by:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left( \beta \cdot T_{i}^{\beta -1}{{e}^{-T_{i}^{\beta }\cdot {{e}^{\mathop{}_{j=0}^{m}{{a}_{j}}{{x}_{i,j}}}}}}{{e}^{\mathop{}_{j=0}^{m}{{a}_{j}}{{x}_{i,j}}}} \right) \\ & & -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( T_{i}^{\prime } \right)}^{\beta }}{{e}^{\mathop{}_{j=0}^{m}{{a}_{j}}{{x}_{i,j}}}}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & R_{Li}^{\prime \prime }= & {{e}^{-T_{Li}^{\prime \prime \beta }{{e}^{\underset{j=0}{\mathop{\overset{n}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}}}}} \\ & R_{Ri}^{\prime \prime }= & {{e}^{-T_{Ri}^{\prime \prime \beta }{{e}^{\underset{j=0}{\mathop{\overset{n}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}}}}} \end{align} }[/math]

Solving for the parameters that maximize Eqn. (PH LKV) will yield the parameters for the PH-Weibull model. Note that for [math]\displaystyle{ \beta }[/math] = 1, Eqn. (PH LKV) becomes the likelihood function for the PH-exponential model, which is similar to the original form of the proportional hazards model proposed by Cox [28].
Note that the likelihood function given by Eqn. (GLL-LK) is very similar to the likelihood function for the proportional hazards-Weibull model given by Eqn. (PH LKV). In particular, the shape parameter of the Weibull distribution can be included in the regression coefficients of Eqn. (13) as follows:

[math]\displaystyle{ {{a}_{i,PH}}=-\beta \cdot {{a}_{i,GLL}} }[/math]

where:

• [math]\displaystyle{ {{a}_{i,PH}} }[/math] are the parameters of the PH model.

• [math]\displaystyle{ {{a}_{i,GLL}} }[/math] are the parameters of the general log-linear model.

In this case, the likelihood functions given by Eqns. (PH LKV) and (GLL-LK) are identical. Therefore, if no transformation on the covariates is performed, the parameter values that maximize Eqn. (GLL-LK) also maximize the likelihood function for the proportional hazards-Weibull (PHW) model with parameters given by Eqn. (GLL Parameters). Note that for [math]\displaystyle{ \beta }[/math] = 1 (exponential life distribution), Eqns. (PH LKV) and (GLL-LK) are identical, and [math]\displaystyle{ {{a}_{i,PH}}=-{{a}_{i,GLL}}. }[/math]

Indicator Variables

Another advantage of the models presented in this chapter is that they allow for simultaneous analysis of continuous and categorical variables. Categorical variables are variables that take on discrete values such as the lot designation for products from different manufacturing lots. In this example, lot is a categorical variable, and it can be expressed in terms of indicator variables. Indicator variables only take a value of 1 or 0. For example, consider a sample of test units. A number of these units were obtained from Lot 1, others from Lot 2, and the rest from Lot 3. These three lots can be represented with the use of indicator variables, as follows:
• Define two indicator variables, [math]\displaystyle{ {{X}_{1}} }[/math] and [math]\displaystyle{ {{X}_{2}}. }[/math]

• For the units from Lot 1, [math]\displaystyle{ {{X}_{1}}=1, }[/math] and [math]\displaystyle{ {{X}_{2}}=0. }[/math]

• For the units from Lot 2, [math]\displaystyle{ {{X}_{1}}=0, }[/math] and [math]\displaystyle{ {{X}_{2}}=1. }[/math]

• For the units from Lot 3, [math]\displaystyle{ {{X}_{1}}=0, }[/math] and [math]\displaystyle{ {{X}_{2}}=0. }[/math]

Assume that an accelerated test was performed with these units, and temperature was the accelerated stress. In this case, the GLL relationship can be used to analyze the data. From Eqn. (GLL1) we get:

[math]\displaystyle{ L(\underline{X})={{e}^{{{\alpha }_{0}}+{{\alpha }_{1}}{{X}_{1}}+{{\alpha }_{2}}{{X}_{2}}+{{\alpha }_{3}}{{X}_{3}}}} }[/math]

where:

• [math]\displaystyle{ {{X}_{1}} }[/math] and [math]\displaystyle{ {{X}_{2}} }[/math] are the indicator variables, as defined above.

• [math]\displaystyle{ {{X}_{3}}=\tfrac{1}{T}, }[/math] where [math]\displaystyle{ T }[/math] is the temperature.

The data can now be entered in ALTA PRO and, with the assumption of an underlying life distribution and using MLE, the parameters of this model can be obtained.