Comparing Life Data Sets: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{template:LDABOOK|24|Comparing Life Data Sets}} | {{template:LDABOOK|24|Comparing Life Data Sets}} | ||
==Tests of Comparison== | |||
It is often desirable to be able to compare two sets of reliability or life data in order to determine which of the data sets has a more favorable life distribution. The units from which the data are obtained could either be from two alternate designs, alternate manufacturers or alternate lots or assembly lines. Many methods are available in statistical literature for doing this when the units come from a complete sample, i.e. a sample with no censoring. This process becomes a little more difficult when dealing with data sets that have censoring, or when trying to compare two data sets that have different distributions. In general, the problem boils down to that of being able to determine any statistically significant difference between the two samples of potentially censored data from two possibly different populations. This section discusses some of the methods that are applicable to censored data, and are available in Weibull++. | It is often desirable to be able to compare two sets of reliability or life data in order to determine which of the data sets has a more favorable life distribution. The units from which the data are obtained could either be from two alternate designs, alternate manufacturers or alternate lots or assembly lines. Many methods are available in statistical literature for doing this when the units come from a complete sample, i.e. a sample with no censoring. This process becomes a little more difficult when dealing with data sets that have censoring, or when trying to compare two data sets that have different distributions. In general, the problem boils down to that of being able to determine any statistically significant difference between the two samples of potentially censored data from two possibly different populations. This section discusses some of the methods that are applicable to censored data, and are available in Weibull++. | ||
===Simple Plotting=== | |||
One popular graphical method for making this determination involves plotting the data with confidence bounds and seeing whether the bounds overlap, or separate, at the point of interest. This can be effective for comparisons at a given point in time or a given reliability level, but it is difficult to assess the overall behavior of the two distributions, as the confidence bounds may overlap at some points and be far apart at others. This can be easily done using the MultiPlot feature in Weibull++. | One popular graphical method for making this determination involves plotting the data with confidence bounds and seeing whether the bounds overlap, or separate, at the point of interest. This can be effective for comparisons at a given point in time or a given reliability level, but it is difficult to assess the overall behavior of the two distributions, as the confidence bounds may overlap at some points and be far apart at others. This can be easily done using the MultiPlot feature in Weibull++. | ||
===Using Contour Plots=== | |||
To determine whether two data sets are significantly different and at what confidence level, one can utilize the contour plots provided in Weibull++. By overlaying two contour plots from two different data sets (analyzed using the same distribution) at the same confidence level, one can visually assess whether the data sets are significantly different at that confidence level if there is no overlap on the contours. The disadvantage of this method is that the same distribution must be fitted to both data sets. | To determine whether two data sets are significantly different and at what confidence level, one can utilize the contour plots provided in Weibull++. By overlaying two contour plots from two different data sets (analyzed using the same distribution) at the same confidence level, one can visually assess whether the data sets are significantly different at that confidence level if there is no overlap on the contours. The disadvantage of this method is that the same distribution must be fitted to both data sets. | ||
==== Example 15==== | ==== Example 15==== | ||
The following data represent the times-to-failure for a product. Certain modifications were made to this product in order to improve its reliability. Reliability engineers are trying to determine whether the improvements were significant in improving the reliability. | The following data represent the times-to-failure for a product. Certain modifications were made to this product in order to improve its reliability. Reliability engineers are trying to determine whether the improvements were significant in improving the reliability. | ||
<math>\overset{\text{Old Design}}{\mathop{\begin{array}{*{35}{l}} | |||
::<math>\overset{\text{Old Design}}{\mathop{\begin{array}{*{35}{l}} | |||
\text{2} & \text{2} & \text{3} & \text{4} & \text{6} & \text{9} \\ | \text{2} & \text{2} & \text{3} & \text{4} & \text{6} & \text{9} \\ | ||
\text{9} & \text{11} & \text{17} & \text{17} & \text{19} & \text{21} \\ | \text{9} & \text{11} & \text{17} & \text{17} & \text{19} & \text{21} \\ | ||
| Line 17: | Line 19: | ||
::<math>\overset{\text{New Design}}{\mathop{\begin{array}{*{35}{l}} | |||
\text{15} & \text{32} & \text{61} & \text{67} & \text{75} \\ | \text{15} & \text{32} & \text{61} & \text{67} & \text{75} \\ | ||
\text{116} & \text{148} & \text{178} & \text{181} & \text{183} \\ | \text{116} & \text{148} & \text{178} & \text{181} & \text{183} \\ | ||
\end{array}}}\,</math> | \end{array}}}\,</math> | ||
At what significant level can the engineers claim that the two designs are different? | At what significant level can the engineers claim that the two designs are different? | ||
==== Solution to Example 15==== | ===== Solution to Example 15===== | ||
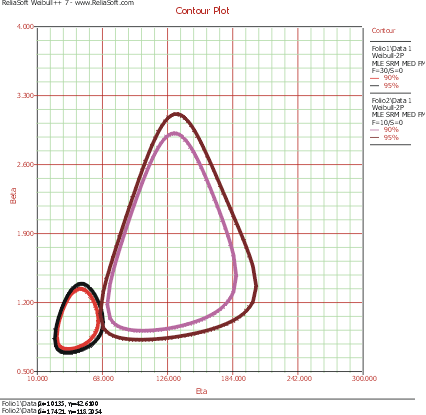
For both data sets the two-parameter Weibull distribution best fits the data. The contour plots were generated and overlaid on a MultiPlot. | For both data sets the two-parameter Weibull distribution best fits the data. The contour plots were generated and overlaid on a MultiPlot. | ||
<math></math> | <math></math> | ||
[[File:lda24.1.gif|center]] | |||
From this plot, it can be seen that there is an overlap at the 95% confidence level and that there is no overlap at the 90% confidence level. It can then be concluded that the new design is better at the 90% confidence level. If a analyst wanted to know at exactly what confidence the two contour plots meet, she would have to incrementally raise the confidence level from 90% until the two plots met. In fact, this search process has been automated by the Confidence Level Detector utility. | From this plot, it can be seen that there is an overlap at the 95% confidence level and that there is no overlap at the 90% confidence level. It can then be concluded that the new design is better at the 90% confidence level. If a analyst wanted to know at exactly what confidence the two contour plots meet, she would have to incrementally raise the confidence level from 90% until the two plots met. In fact, this search process has been automated by the Confidence Level Detector utility. | ||
Revision as of 18:34, 26 July 2011
Tests of Comparison
It is often desirable to be able to compare two sets of reliability or life data in order to determine which of the data sets has a more favorable life distribution. The units from which the data are obtained could either be from two alternate designs, alternate manufacturers or alternate lots or assembly lines. Many methods are available in statistical literature for doing this when the units come from a complete sample, i.e. a sample with no censoring. This process becomes a little more difficult when dealing with data sets that have censoring, or when trying to compare two data sets that have different distributions. In general, the problem boils down to that of being able to determine any statistically significant difference between the two samples of potentially censored data from two possibly different populations. This section discusses some of the methods that are applicable to censored data, and are available in Weibull++.
Simple Plotting
One popular graphical method for making this determination involves plotting the data with confidence bounds and seeing whether the bounds overlap, or separate, at the point of interest. This can be effective for comparisons at a given point in time or a given reliability level, but it is difficult to assess the overall behavior of the two distributions, as the confidence bounds may overlap at some points and be far apart at others. This can be easily done using the MultiPlot feature in Weibull++.
Using Contour Plots
To determine whether two data sets are significantly different and at what confidence level, one can utilize the contour plots provided in Weibull++. By overlaying two contour plots from two different data sets (analyzed using the same distribution) at the same confidence level, one can visually assess whether the data sets are significantly different at that confidence level if there is no overlap on the contours. The disadvantage of this method is that the same distribution must be fitted to both data sets.
Example 15
The following data represent the times-to-failure for a product. Certain modifications were made to this product in order to improve its reliability. Reliability engineers are trying to determine whether the improvements were significant in improving the reliability.
- [math]\displaystyle{ \overset{\text{Old Design}}{\mathop{\begin{array}{*{35}{l}} \text{2} & \text{2} & \text{3} & \text{4} & \text{6} & \text{9} \\ \text{9} & \text{11} & \text{17} & \text{17} & \text{19} & \text{21} \\ \text{23} & \text{28} & \text{33} & \text{34} & \text{34} & \text{37} \\ \text{38} & \text{40} & \text{45} & \text{55} & \text{56} & \text{57} \\ \text{67} & \text{76} & \text{90} & \text{115} & \text{126} & \text{197} \\ \end{array}}}\, }[/math]
- [math]\displaystyle{ \overset{\text{New Design}}{\mathop{\begin{array}{*{35}{l}} \text{15} & \text{32} & \text{61} & \text{67} & \text{75} \\ \text{116} & \text{148} & \text{178} & \text{181} & \text{183} \\ \end{array}}}\, }[/math]
At what significant level can the engineers claim that the two designs are different?
Solution to Example 15
For both data sets the two-parameter Weibull distribution best fits the data. The contour plots were generated and overlaid on a MultiPlot.
[math]\displaystyle{ }[/math]
From this plot, it can be seen that there is an overlap at the 95% confidence level and that there is no overlap at the 90% confidence level. It can then be concluded that the new design is better at the 90% confidence level. If a analyst wanted to know at exactly what confidence the two contour plots meet, she would have to incrementally raise the confidence level from 90% until the two plots met. In fact, this search process has been automated by the Confidence Level Detector utility.
Confidence Level Detector
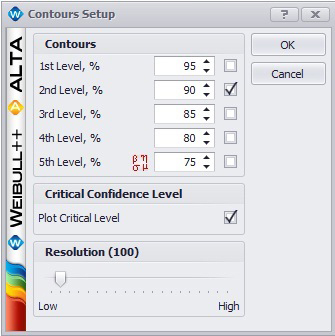
The Confidence Level Detector (CLD) utility is located as an option in the Contour Plot Setup window. To activate the utility, check the “Plot Critical Level” box as shown in the figure below.
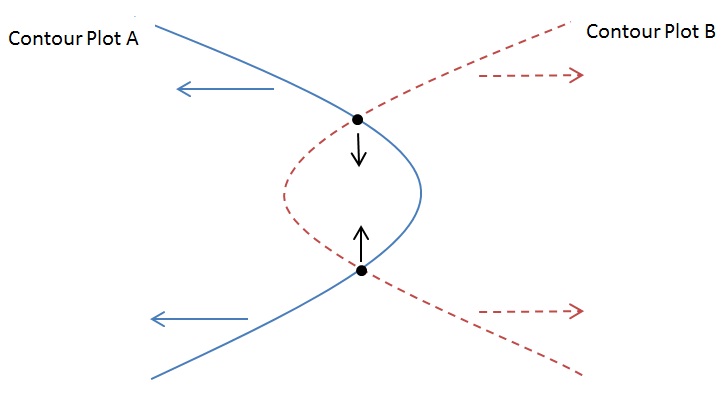
The CLD utility determines the confidence level at which the contour plots of two data sets meet at a single point. This is the minimum confidence level at which the contour plots of the two different data sets overlap. At any confidence level below this minimum confidence level, the contour plots of the two data sets will not overlap and there will be a statistically significant difference between the two populations at that level.
Let and be the 99% two-sided lower bounds on for populations 1 and 2, respectively, and let and be the 99% two-sided upper bounds on for populations 1 and 2, respectively. 99% is used as the starting confidence level to make sure that the contour plots are large enough to overlap. The confidence levels are decreased, which in turn decreases the size of the contour plots of the two populations, causing the intersection points of the two contour plots move towards each other, as illustrated in the figure below.
The confidence level is decreased until the contour plots meet at a single point.
Estimating [math]\displaystyle{ P\left[ {{t}_{2}}\ge {{t}_{1}} \right] }[/math] Using the Comparison Wizard
Another methodology, suggested by Gerald G. Brown and Herbert C. Rutemiller, is to estimate the probability of whether the times-to-failure of one population are better or worse than the times-to-failure of the second. The equation used to estimate this probability is given by:
[math]\displaystyle{ P\left[ {{t}_{2}}\ge {{t}_{1}} \right]=\mathop{}_{0}^{\infty }{{f}_{1}}(t)\cdot {{R}_{2}}(t)\cdot dt }[/math]
where [math]\displaystyle{ {{f}_{1}}(t) }[/math] is the [math]\displaystyle{ pdf }[/math] of the first distribution and [math]\displaystyle{ {{R}_{2}}(t) }[/math] is the reliability function of the second distribution. The evaluation of the superior data set is based on whether this probability is smaller or greater than 0.5. If the probability is equal to 0.5, that is equivalent to saying the two distributions are identical.
If given two alternate designs with life test data, where X and Y represent the life test data from two different populations, and if we simply wanted to choose the component at time [math]\displaystyle{ t }[/math] with the higher reliability, one choice would be to select the component with the higher reliability at time [math]\displaystyle{ t }[/math] . However, if we wanted to design a product as long-lived as possible, we would want to calculate the probability that the entire distribution of one product is better than the other and choose X or Y when this probability is above or below 0.50 respectively.
The statement that the probability that X is greater or equal to Y can be interpreted as follows:
• If [math]\displaystyle{ P=0.50 }[/math] , then the statement is equivalent to saying that both X and Y are equal.
• If [math]\displaystyle{ P\lt 0.50 }[/math] or, for example, [math]\displaystyle{ P=0.10 }[/math] , then the statement is equivalent to saying that [math]\displaystyle{ P=1-0.10=0.90 }[/math] , or Y is better than X with a 90% probability.
Weibull++'s Comparison Wizard allows you to perform such calculations. The disadvantage of this method is that the sample sizes are not taken into account, thus one should avoid using this method of comparison when the sample sizes are different.
Example 16
Using the data presented in Example 15, use Weibull++'s Comparison Wizard to estimate the probability that units from the new design will outlast units from the old design.
Solution to Example 16
After entering the Example 15's data sets into two different folios (or data sheets within the same folio) and analyzing them (in this case, the two data sets were analyzed using the two-parameter distribution and MLE), select Tests of Comparison from the Tools menu to accessthe Comparison Wizard. Specify the data sets that are being compared:
[math]\displaystyle{ }[/math]
Click Compare. The result of the comparison is displayed in the next window.
[math]\displaystyle{ }[/math]