Temperature-Nonthermal (TNT)-Weibull Model: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
No edit summary
Line 122: Line 122:


[[image:Two Stress GLL Weibull_Analysis Summary GLL.png|center]]
[[image:Two Stress GLL Weibull_Analysis Summary GLL.png|center]]
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">'''Result in ALTA'''</div>
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">'''Results in ALTA'''</div>




Revision as of 18:08, 16 June 2014

ALTA Reference Examples Banner.png


New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.



Temperature-Nonthermal (TNT)-Weibull Model

This example compares the results for the temperature-nonthermal life-stress relationship with a Weibull distribution.


Reference Case

Data is from Table 7.10 on page 300 in book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.


Data

Temperature and switching rate are the two stresses used in the accelerated life test for a type of 18-V compact electromagnetic relay. The cycles to failure are provided next.

Number in Group State F/S Time to State Temperature (F) Switching Rate Subset ID Number in Group State F/S Time to State Temperature (F) Switching Rate Subset ID
1 F 47154 337.15 10 1 1 F 29672 398.15 10 3
1 F 51307 337.15 10 1 1 F 38586 398.15 10 3
1 F 86149 337.15 10 1 1 F 47570 398.15 10 3
1 F 89702 337.15 10 1 1 F 56979 398.15 10 3
1 F 90044 337.15 10 1 6 S 57600 398.15 10 3
1 F 129795 337.15 10 1 1 F 7151 398.15 30 4
1 F 218384 337.15 10 1 1 F 11966 398.15 30 4
1 F 223994 337.15 10 1 1 F 16772 398.15 30 4
1 F 227383 337.15 10 1 1 F 17691 398.15 30 4
1 F 229354 337.15 10 1 1 F 18088 398.15 30 4
1 F 244685 337.15 10 1 1 F 18446 398.15 30 4
1 F 253690 337.15 10 1 1 F 19442 398.15 30 4
1 F 270150 337.15 10 1 1 F 25952 398.15 30 4
1 F 281499 337.15 10 1 1 F 29154 398.15 30 4
59 S 288000 337.15 10 1 1 F 30236 398.15 30 4
1 F 45663 337.15 30 2 1 F 33433 398.15 30 4
1 F 123237 337.15 30 2 1 F 33492 398.15 30 4
1 F 192073 337.15 30 2 1 F 39094 398.15 30 4
1 F 212696 337.15 30 2 1 F 51761 398.15 30 4
1 F 304669 337.15 30 2 1 F 53926 398.15 30 4
1 F 323332 337.15 30 2 1 F 57124 398.15 30 4
1 F 346814 337.15 30 2 1 F 61833 398.15 30 4
1 F 452855 337.15 30 2 1 F 67618 398.15 30 4
1 F 480915 337.15 30 2 1 F 70177 398.15 30 4
1 F 496672 337.15 30 2 1 F 71534 398.15 30 4
1 F 557136 337.15 30 2 1 F 79047 398.15 30 4
1 F 570003 337.15 30 2 1 F 91295 398.15 30 4
1 F 12019 398.15 10 3 1 F 92005 398.15 30 4
1 F 18590 398.15 10 3


Result

The following temperature non-thermal life stress relationship is used:

[math]\displaystyle{ \,\!L\left ( f,T \right )=Af^{B}e^{\left ( \frac{E_{a}}{kT} \right )} }[/math]

where [math]\displaystyle{ \,\!f }[/math] is the switching rate, [math]\displaystyle{ \,\!T }[/math] is temperature. [math]\displaystyle{ \,\!L\left ( f,T \right ) }[/math] is the life characteristic affected by the two stresses. In ALTA, this life-stress relationship is called the "temperature non-thermal" model. This relationship also can be expressed as the following:

[math]\displaystyle{ \,\!ln\left ( L\left ( x_{1},x_{2} \right ) \right )=\alpha _{0}+\alpha _{1}x_{1}+\alpha _{2}x_{2} }[/math]

where [math]\displaystyle{ \,\!x_{1}=\frac{1}{T} }[/math] and [math]\displaystyle{ \,\!x_{2}=ln\left ( f \right ) }[/math] .

The failure time distribution is a Weibull distribution. The book has the following results:

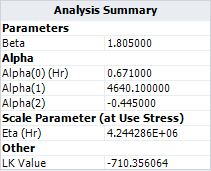
  • The maximum likelihood estimation (MLE) results for the parameters are: [math]\displaystyle{ \,\!\alpha _{0}=0.671 }[/math] , [math]\displaystyle{ \,\!\alpha _{1}=4640.1 }[/math] , [math]\displaystyle{ \,\!\alpha _{2}=-0.445 }[/math] and [math]\displaystyle{ \,\!\beta =1.805 }[/math].
  • The eta parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as [math]\displaystyle{ \,\!4.244\times 10^{6} }[/math].
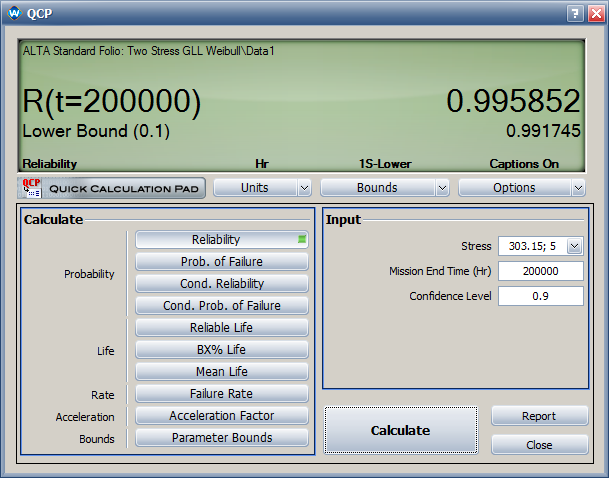
  • The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992.
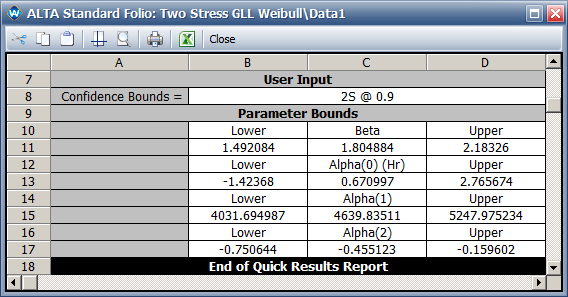
  • The two-sided 90% confidence interval for parameter [math]\displaystyle{ \,\!\alpha _{2} }[/math] is [-0.751, -0.160].


Results in ALTA

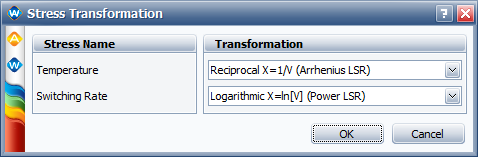
We will first perform the analysis using the general log-linear (GLL) life-stress relationship, and then compare its results with the temperature-nonthermal model (TNT) life-stress relationship.

Two Stress GLL Weibull Stress Transform.png


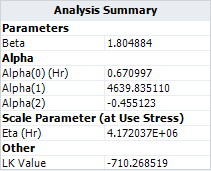
  • Based on this model, the maximum likelihood estimation (MLE) results for the parameters are:
Two Stress GLL Weibull Analysis Summary GLL.png
Results in ALTA


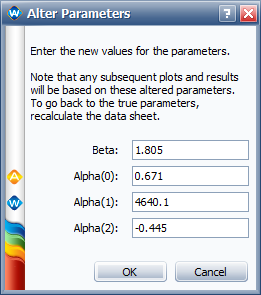
These results are slightly different from the results given in the book (especially for [math]\displaystyle{ \,\!\alpha _{2} }[/math]). To see what the log likelihood value (LK Value) would be if we used the parameter values in the book, we use the Alter Parameters tool, as shown next.
Two Stress GLL Weibull Alter Parameters.png


The resulting LK Value for the altered parameters is -710.356064, as shown next.
Two Stress GLL Weibull Analysis Summary GLL new alpha.png
Altered Parameters


This likelihood value is slightly smaller than the value that was originally calculated in ALTA, which was -710.268519. Therefore, the result in ALTA is better in terms of maximizing the log likelihood value.

Using the parameters originally calculated in ALTA:

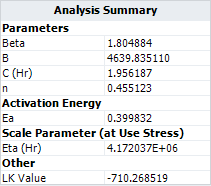
  • The [math]\displaystyle{ \,\!\eta }[/math] parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as [math]\displaystyle{ \,\!4.172\times 10^{6} }[/math] .
  • The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 F) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992, as shown next.
Two Stress GLL Weibull QPC Reliability.png


  • The two-sided 90% confidence interval for parameter [math]\displaystyle{ \,\!\alpha _{2} }[/math] is [-0.751, -0.160], as shown next.
Two Stress GLL Weibull Parameter Bounds.png


Temperature-Nonthermal (TNT)-Weibull Model

If we use the temperature-nonthermal life-stress relationship to analyze the data, the same results would be obtained, as shown in the following picture. Therefore, by selecting the appropriate stress transformations, a general log-linear model can become a temperature-nonthermal model.

Two Stress GLL Weibull Analysis Summary TNT.png
Retrieved from "https://www.reliawiki.com/index.php?title=Temperature-Nonthermal_(TNT)-Weibull_Model&oldid=55867"