|
|
| Line 100: |
Line 100: |
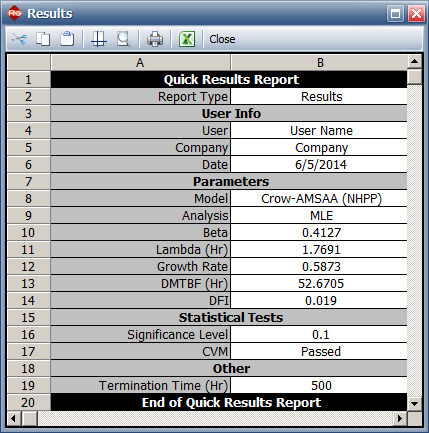
| [[image:CB for Weibull_Results.png|center]] | | [[image:CB for Weibull_Results.png|center]] |
|
| |
|
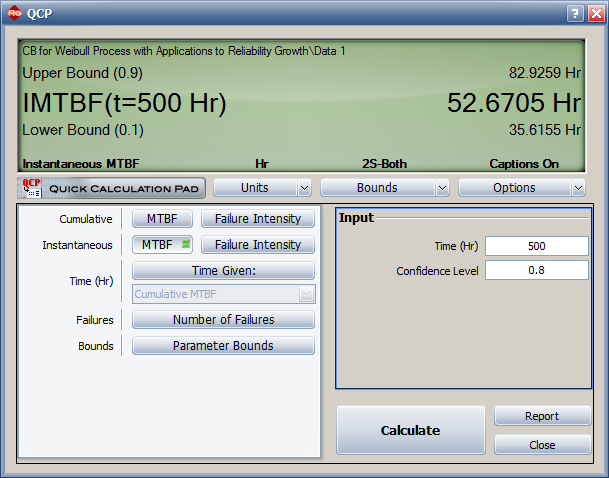
| The intanteous MTBF and its two-sided confidence bounds are: | | The instantaneous MTBF and its two-sided 80% confidence bounds are: |
| [[image:CB for Weibull_QPC.png|center]] | | [[image:CB for Weibull_QPC.png|center]] |
Revision as of 16:24, 13 June 2014
RGA_Reference_Examples_Banner.png
This example compares the results for test-fix-test data (time terminated).
Reference Case
Crow, L.H., Confidence Interval Procedures for the Weibull Process with Applications to Reliability Growth, U.S. Army Material Systems Analysis Activity, 1981.
Data
The following table shows the data.
| 0.2
|
| 4.2
|
| 4.5
|
| 5
|
| 5.4
|
| 6.1
|
| 7.9
|
| 14.8
|
| 19.2
|
| 48.6
|
| 85.8
|
| 108.9
|
| 127.2
|
| 129.8
|
| 150.1
|
| 159.7
|
| 227.4
|
| 244.7
|
| 262.7
|
| 315.3
|
| 329.6
|
| 404.3
|
| 486.2
|
Termination Time = 500 hours
Result
The book has the following results:
- Beta = 0.413, Lambda = 1.769
- Confidence Bounds on DMTBF (CL = 80%) = (35.6, 82.9)
Results in RGA
In RGA, the following equations are used to calculate [math]\displaystyle{ \beta\,\! }[/math] and [math]\displaystyle{ \lambda\,\! }[/math].
- [math]\displaystyle{ \begin{align}
\hat{\beta }=&\frac{N}{{N\ln T^{*}}-\sum_{i=1}^{N}T_{i}}\\
\\
=&\frac{23}{{23\cdot \ln \left ( 500 \right )}-87.2106}\\
\\
=&0.4127
\end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align}
\hat{\lambda }=&\frac{N}{T^{*\beta }}\\
\\
=&\frac{23}{500^{0.4127}}\\
\\
=&1.7691
\end{align}\,\! }[/math]
The instantaneous MTBF and its two-sided 80% confidence bounds are:
