Temperature-Nonthermal (TNT)-Weibull Model: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
No edit summary
Line 94: Line 94:
::<math>\,\!L\left ( f,T \right )=Af^{B}e^{\left ( \frac{E_{a}}{kT} \right )}</math>
::<math>\,\!L\left ( f,T \right )=Af^{B}e^{\left ( \frac{E_{a}}{kT} \right )}</math>


where <math>\,\!f</math> is the switching rate, <math>\,\!T</math> is temperature. <math>\,\!L\left ( f,T \right )</math> is the life characteristic affected by the two stresses. This relationship is called temperature non-thermal model in ALTA.
where <math>\,\!f</math> is the switching rate, <math>\,\!T</math> is temperature. <math>\,\!L\left ( f,T \right )</math> is the life characteristic affected by the two stresses. In ALTA, this life-stress relationship is called the "temperature non-thermal" model.  
 
 
This relationship also can be expressed as the following:
This relationship also can be expressed as the following:


Line 129: Line 127:




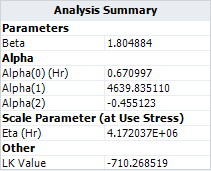
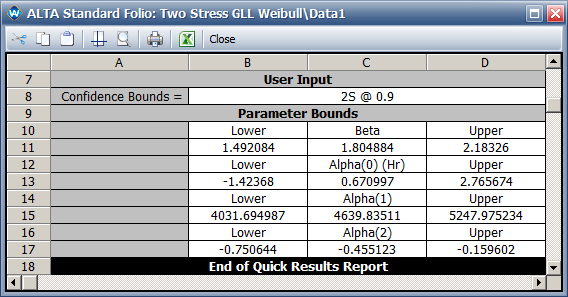
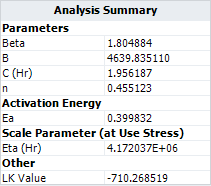
:This likelihood value is slightly smaller than the value given in ALTA which is -710.268519. Therefore, the result in ALTA is better in terms of maximizing the log likelihood value.
:This likelihood value is slightly smaller than the value given in ALTA, which is -710.268519. Therefore, the result in ALTA is better in terms of maximizing the log likelihood value.


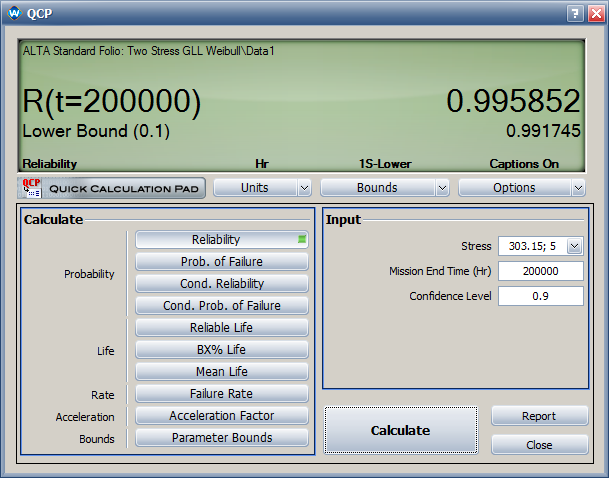
*The η parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as <math>\,\!4.172\times 10^{6}</math> .
*The η parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as <math>\,\!4.172\times 10^{6}</math> .
Line 147: Line 145:




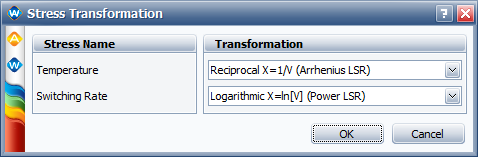
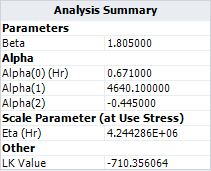
If the temperature-Nonthermal relationship is used directly, the same results will be obtained. The following is the estimated model parameters for the temperature-nonthermal model in ALTA. By doing the right transformations for the stresses, a general log linear model can become a temperature-nonthermal model.
If the temperature-Nonthermal relationship is used directly, the same results will be obtained. The following is the estimated model parameters for the temperature-nonthermal model in ALTA. By doing the right transformations for the stresses, a general log-linear model can become a temperature-nonthermal model.
 


[[image:Two Stress GLL Weibull_Analysis Summary TNT.png|center]]
[[image:Two Stress GLL Weibull_Analysis Summary TNT.png|center]]

Revision as of 15:29, 13 June 2014

ALTA_Reference_Examples_Banner.png

ALTA_Reference_Examples

This example compares the results for the temperature-nonthermal life-stress relationship with a Weibull distribution.


Reference Case

Data is from Table 7.10 on page 300 in book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.


Data

Temperature and switching rate are the two stresses used in the accelerated life test for a type of 18-V compact electromagnetic relay. The cycles to failure are provided next.

Number in Group State F/S Time to State Temperature (F) Switching Rate Subset ID Number in Group State F/S Time to State Temperature (F) Switching Rate Subset ID
1 F 47154 337.15 10 1 1 F 29672 398.15 10 3
1 F 51307 337.15 10 1 1 F 38586 398.15 10 3
1 F 86149 337.15 10 1 1 F 47570 398.15 10 3
1 F 89702 337.15 10 1 1 F 56979 398.15 10 3
1 F 90044 337.15 10 1 6 S 57600 398.15 10 3
1 F 129795 337.15 10 1 1 F 7151 398.15 30 4
1 F 218384 337.15 10 1 1 F 11966 398.15 30 4
1 F 223994 337.15 10 1 1 F 16772 398.15 30 4
1 F 227383 337.15 10 1 1 F 17691 398.15 30 4
1 F 229354 337.15 10 1 1 F 18088 398.15 30 4
1 F 244685 337.15 10 1 1 F 18446 398.15 30 4
1 F 253690 337.15 10 1 1 F 19442 398.15 30 4
1 F 270150 337.15 10 1 1 F 25952 398.15 30 4
1 F 281499 337.15 10 1 1 F 29154 398.15 30 4
59 S 288000 337.15 10 1 1 F 30236 398.15 30 4
1 F 45663 337.15 30 2 1 F 33433 398.15 30 4
1 F 123237 337.15 30 2 1 F 33492 398.15 30 4
1 F 192073 337.15 30 2 1 F 39094 398.15 30 4
1 F 212696 337.15 30 2 1 F 51761 398.15 30 4
1 F 304669 337.15 30 2 1 F 53926 398.15 30 4
1 F 323332 337.15 30 2 1 F 57124 398.15 30 4
1 F 346814 337.15 30 2 1 F 61833 398.15 30 4
1 F 452855 337.15 30 2 1 F 67618 398.15 30 4
1 F 480915 337.15 30 2 1 F 70177 398.15 30 4
1 F 496672 337.15 30 2 1 F 71534 398.15 30 4
1 F 557136 337.15 30 2 1 F 79047 398.15 30 4
1 F 570003 337.15 30 2 1 F 91295 398.15 30 4
1 F 12019 398.15 10 3 1 F 92005 398.15 30 4
1 F 18590 398.15 10 3


Result

The following temperature non-thermal life stress relationship is used:

[math]\displaystyle{ \,\!L\left ( f,T \right )=Af^{B}e^{\left ( \frac{E_{a}}{kT} \right )} }[/math]

where [math]\displaystyle{ \,\!f }[/math] is the switching rate, [math]\displaystyle{ \,\!T }[/math] is temperature. [math]\displaystyle{ \,\!L\left ( f,T \right ) }[/math] is the life characteristic affected by the two stresses. In ALTA, this life-stress relationship is called the "temperature non-thermal" model. This relationship also can be expressed as the following:

[math]\displaystyle{ \,\!ln\left ( L\left ( x_{1},x_{2} \right ) \right )=\alpha _{0}+\alpha _{1}x_{1}+\alpha _{2}x_{2} }[/math]

where [math]\displaystyle{ \,\!x_{1}=\frac{1}{T} }[/math] and [math]\displaystyle{ \,\!x_{2}=ln\left ( f \right ) }[/math] . This is the General log-linear model with the proper stress transformation in ALTA.

Two Stress GLL Weibull Stress Transform.png


The failure time distribution is a Weibull distribution. The book has the following results:

  • The maximum likelihood estimation (MLE) results for the parameters are: [math]\displaystyle{ \,\!\alpha _{0}=0.671 }[/math] , [math]\displaystyle{ \,\!\alpha _{1}=4640.1 }[/math] , [math]\displaystyle{ \,\!\alpha _{2}=-0.445 }[/math] and [math]\displaystyle{ \,\!\beta =1.805 }[/math].
  • The eta parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as [math]\displaystyle{ \,\!4.244\times 10^{6} }[/math].
  • The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992.
  • The two-sided 90% confidence interval for parameter [math]\displaystyle{ \,\!\alpha _{2} }[/math] is [-0.751, -0.160].


Results in ALTA

  • The maximum likelihood estimation (MLE) results for the parameters are:
Two Stress GLL Weibull Analysis Summary GLL.png


These results (especially [math]\displaystyle{ \,\!\alpha _{2} }[/math]) are slightly different from the one given in the book. If we use the results in the book, then the calculated log likelihood value is -710.354601 as given below.
Two Stress GLL Weibull Analysis Summary GLL new alpha.png


This likelihood value is slightly smaller than the value given in ALTA, which is -710.268519. Therefore, the result in ALTA is better in terms of maximizing the log likelihood value.
  • The η parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as [math]\displaystyle{ \,\!4.172\times 10^{6} }[/math] .


Two Stress GLL Weibull Eta.png


  • The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 F) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992.
Two Stress GLL Weibull QPC Reliability.png


  • The two-sided 90% confidence interval for parameter [math]\displaystyle{ \,\!\alpha _{2} }[/math] is [-0.751, -0.160].
Two Stress GLL Weibull Parameter Bounds.png


If the temperature-Nonthermal relationship is used directly, the same results will be obtained. The following is the estimated model parameters for the temperature-nonthermal model in ALTA. By doing the right transformations for the stresses, a general log-linear model can become a temperature-nonthermal model.


Two Stress GLL Weibull Analysis Summary TNT.png
Retrieved from "https://www.reliawiki.com/index.php?title=Temperature-Nonthermal_(TNT)-Weibull_Model&oldid=55732"