|
|
| Line 102: |
Line 102: |
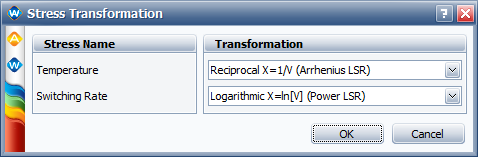
| where <math>\,\!x_{1}=\frac{1}{T}</math> and <math>\,\!x_{2}=ln\left ( f \right )</math> . This is the General log-linear model with the proper stress transformation in ALTA. | | where <math>\,\!x_{1}=\frac{1}{T}</math> and <math>\,\!x_{2}=ln\left ( f \right )</math> . This is the General log-linear model with the proper stress transformation in ALTA. |
|
| |
|
| [[image: .png|center]] | | [[image:Two Stress GLL Weibull_Stress Transform.png|center]] |
| | |
|
| |
|
| The failure time distribution is a Weibull distribution. The book has the following results: | | The failure time distribution is a Weibull distribution. The book has the following results: |
| Line 119: |
Line 120: |
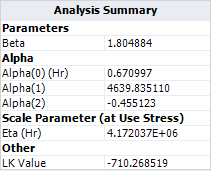
| *The maximum likelihood estimation (MLE) results for the parameters are: | | *The maximum likelihood estimation (MLE) results for the parameters are: |
|
| |
|
| [[image: .png|center]] | | [[image:Two Stress GLL Weibull_Analysis Summary GLL.png|center]] |
|
| |
|
| These results (especially <math>\,\!\alpha _{2}</math>) are slightly different from the one given in the book. If we use the results in the book, then the calculated log likelihood value is -710.354601 as given below. | | These results (especially <math>\,\!\alpha _{2}</math>) are slightly different from the one given in the book. If we use the results in the book, then the calculated log likelihood value is -710.354601 as given below. |
| Line 126: |
Line 127: |
|
| |
|
| This likelihood value is slightly smaller than the value given in ALTA which is -710.268519. Therefore, the result in ALTA is better in terms of maximizing the log likelihood value. | | This likelihood value is slightly smaller than the value given in ALTA which is -710.268519. Therefore, the result in ALTA is better in terms of maximizing the log likelihood value. |
|
| |
|
| |
| [[image: .png|center]]
| |
|
| |
|
| *The η parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as <math>\,\!4.172\times 10^{6}</math> . | | *The η parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as <math>\,\!4.172\times 10^{6}</math> . |
|
| |
|
| | | [[image:Two Stress GLL Weibull_Eta.png|center]] |
| [[image: .png|center]] | |
| | |
|
| |
|
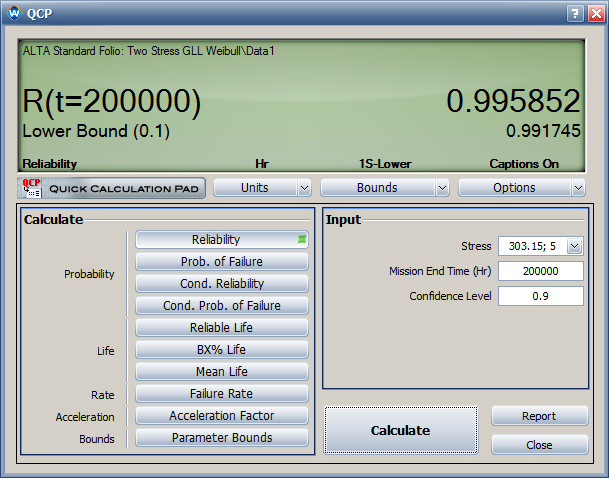
| *The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 F) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992. | | *The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 F) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992. |
|
| |
|
| [[image: .png|center]] | | [[image:Two Stress GLL Weibull_QPC Reliability.png|center]] |
| | |
| | |
|
| |
|
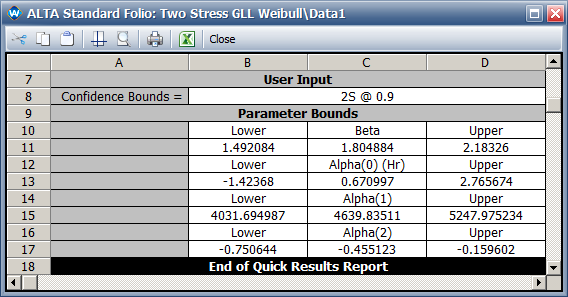
| *The two-sided 90% confidence interval for parameter <math>\,\!\alpha _{2}</math> is [-0.751, -0.160]. | | *The two-sided 90% confidence interval for parameter <math>\,\!\alpha _{2}</math> is [-0.751, -0.160]. |
|
| |
|
|
| |
|
| [[image: .png|center]] | | [[image:Two Stress GLL Weibull_Parameter Bounds.png|center]] |
|
| |
|
|
| |
|
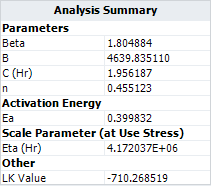
| If the temperature-Nonthermal relationship is used directly, the same results will be obtained. The following is the estimated model parameters for the temperature-nonthermal model in ALTA. By doing the right transformations for the stresses, a general log linear model can become a temperature-nonthermal model. | | If the temperature-Nonthermal relationship is used directly, the same results will be obtained. The following is the estimated model parameters for the temperature-nonthermal model in ALTA. By doing the right transformations for the stresses, a general log linear model can become a temperature-nonthermal model. |
|
| |
|
| [[image: .png|center]] | | [[image:Two Stress GLL Weibull_Analysis Summary TNT.png|center]] |
ALTA_Reference_Examples_Banner.png
This example validates the calculation of the temperature-nonthermal relationship for Weibull distribution.
Reference Case
Data is from Table 7.10 on page 300 in book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.
Data
Temperature and switching rate are the two stresses used in the accelerated life test for a type of 18-V compact electromagnetic relays. The cycles to failure are provided next.
| Number in Group
|
State F/S
|
Time to State
|
Temperature (F)
|
Switching Rate
|
Subset ID
|
Number in Group
|
State F/S
|
Time to State
|
Temperature (F)
|
Switching Rate
|
Subset ID
|
| 1 |
F |
47154 |
337.15 |
10 |
1 |
1 |
F |
29672 |
398.15 |
10 |
3
|
| 1 |
F |
51307 |
337.15 |
10 |
1 |
1 |
F |
38586 |
398.15 |
10 |
3
|
| 1 |
F |
86149 |
337.15 |
10 |
1 |
1 |
F |
47570 |
398.15 |
10 |
3
|
| 1 |
F |
89702 |
337.15 |
10 |
1 |
1 |
F |
56979 |
398.15 |
10 |
3
|
| 1 |
F |
90044 |
337.15 |
10 |
1 |
6 |
S |
57600 |
398.15 |
10 |
3
|
| 1 |
F |
129795 |
337.15 |
10 |
1 |
1 |
F |
7151 |
398.15 |
30 |
4
|
| 1 |
F |
218384 |
337.15 |
10 |
1 |
1 |
F |
11966 |
398.15 |
30 |
4
|
| 1 |
F |
223994 |
337.15 |
10 |
1 |
1 |
F |
16772 |
398.15 |
30 |
4
|
| 1 |
F |
227383 |
337.15 |
10 |
1 |
1 |
F |
17691 |
398.15 |
30 |
4
|
| 1 |
F |
229354 |
337.15 |
10 |
1 |
1 |
F |
18088 |
398.15 |
30 |
4
|
| 1 |
F |
244685 |
337.15 |
10 |
1 |
1 |
F |
18446 |
398.15 |
30 |
4
|
| 1 |
F |
253690 |
337.15 |
10 |
1 |
1 |
F |
19442 |
398.15 |
30 |
4
|
| 1 |
F |
270150 |
337.15 |
10 |
1 |
1 |
F |
25952 |
398.15 |
30 |
4
|
| 1 |
F |
281499 |
337.15 |
10 |
1 |
1 |
F |
29154 |
398.15 |
30 |
4
|
| 59 |
S |
288000 |
337.15 |
10 |
1 |
1 |
F |
30236 |
398.15 |
30 |
4
|
| 1 |
F |
45663 |
337.15 |
30 |
2 |
1 |
F |
33433 |
398.15 |
30 |
4
|
| 1 |
F |
123237 |
337.15 |
30 |
2 |
1 |
F |
33492 |
398.15 |
30 |
4
|
| 1 |
F |
192073 |
337.15 |
30 |
2 |
1 |
F |
39094 |
398.15 |
30 |
4
|
| 1 |
F |
212696 |
337.15 |
30 |
2 |
1 |
F |
51761 |
398.15 |
30 |
4
|
| 1 |
F |
304669 |
337.15 |
30 |
2 |
1 |
F |
53926 |
398.15 |
30 |
4
|
| 1 |
F |
323332 |
337.15 |
30 |
2 |
1 |
F |
57124 |
398.15 |
30 |
4
|
| 1 |
F |
346814 |
337.15 |
30 |
2 |
1 |
F |
61833 |
398.15 |
30 |
4
|
| 1 |
F |
452855 |
337.15 |
30 |
2 |
1 |
F |
67618 |
398.15 |
30 |
4
|
| 1 |
F |
480915 |
337.15 |
30 |
2 |
1 |
F |
70177 |
398.15 |
30 |
4
|
| 1 |
F |
496672 |
337.15 |
30 |
2 |
1 |
F |
71534 |
398.15 |
30 |
4
|
| 1 |
F |
557136 |
337.15 |
30 |
2 |
1 |
F |
79047 |
398.15 |
30 |
4
|
| 1 |
F |
570003 |
337.15 |
30 |
2 |
1 |
F |
91295 |
398.15 |
30 |
4
|
| 1 |
F |
12019 |
398.15 |
10 |
3 |
1 |
F |
92005 |
398.15 |
30 |
4
|
| 1 |
F |
18590 |
398.15 |
10 |
3 |
|
|
|
|
|
|
Result
The following temperature non-thermal life stress relationship is used:
- [math]\displaystyle{ \,\!L\left ( f,T \right )=Af^{B}e^{\left ( \frac{E_{a}}{kT} \right )} }[/math]
where [math]\displaystyle{ \,\!f }[/math] is the switching rate, [math]\displaystyle{ \,\!T }[/math] is temperature. [math]\displaystyle{ \,\!L\left ( f,T \right ) }[/math] is the life characteristic affected by the two stresses. This relationship is called temperature non-thermal model in ALTA.
This relationship also can be expressed as the following:
- [math]\displaystyle{ \,\!ln\left ( L\left ( x_{1},x_{2} \right ) \right )=\alpha _{0}+\alpha _{1}x_{1}+\alpha _{2}x_{2} }[/math]
where [math]\displaystyle{ \,\!x_{1}=\frac{1}{T} }[/math] and [math]\displaystyle{ \,\!x_{2}=ln\left ( f \right ) }[/math] . This is the General log-linear model with the proper stress transformation in ALTA.
The failure time distribution is a Weibull distribution. The book has the following results:
- The maximum likelihood estimation (MLE) results for the parameters are: [math]\displaystyle{ \,\!\alpha _{0}=0.671 }[/math] , [math]\displaystyle{ \,\!\alpha _{1}=4640.1 }[/math] , [math]\displaystyle{ \,\!\alpha _{2}=-0.445 }[/math] and [math]\displaystyle{ \,\!\beta =1.805 }[/math].
- The eta parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as [math]\displaystyle{ \,\!4.244\times 10^{6} }[/math].
- The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992.
- The two-sided 90% confidence interval for parameter [math]\displaystyle{ \,\!\alpha _{2} }[/math] is [-0.751, -0.160].
Results in ALTA
- The maximum likelihood estimation (MLE) results for the parameters are:
These results (especially [math]\displaystyle{ \,\!\alpha _{2} }[/math]) are slightly different from the one given in the book. If we use the results in the book, then the calculated log likelihood value is -710.354601 as given below.
This likelihood value is slightly smaller than the value given in ALTA which is -710.268519. Therefore, the result in ALTA is better in terms of maximizing the log likelihood value.
- The η parameter in the Weibull distribution at temperature of 30°C (303.15 K) and switching rate of 5 cycles/minute is estimated as [math]\displaystyle{ \,\!4.172\times 10^{6} }[/math] .
- The estimated reliability at 200,000 cycles and temperature of 30°C (303.15 F) and switching rate of 5 cycles/minute is 0.996. Its one-sided lower 90% confidence bound is 0.992.
- The two-sided 90% confidence interval for parameter [math]\displaystyle{ \,\!\alpha _{2} }[/math] is [-0.751, -0.160].
If the temperature-Nonthermal relationship is used directly, the same results will be obtained. The following is the estimated model parameters for the temperature-nonthermal model in ALTA. By doing the right transformations for the stresses, a general log linear model can become a temperature-nonthermal model.
