Lloyd-Lipow Least Squares Example: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 97: | Line 97: | ||
:<math>{{R}_{k}}=0.8104-\frac{0.2201}{k}\,\!</math> | :<math>{{R}_{k}}=0.8104-\frac{0.2201}{k}\,\!</math> | ||
</li> | |||
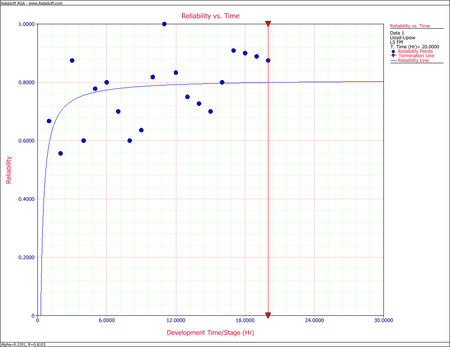
<li>The reliabilities from the raw data and the reliabilities predicted from the Lloyd-Lipow reliability growth model are given in the last two columns of the table. The figure below shows the plot. Based on the given data, the model cannot do much more than to basically fit a line through the middle of the points. | |||
[[Image:rga6.1.png|center|450px]] | |||
</li> | |||
</ol> | |||
Revision as of 19:46, 29 May 2014
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability Growth and Repairable System Analysis Reference.
After a 20-stage reliability development test program, 20 groups of success/failure data were obtained and are given in the table below. Do the following:
- Fit the Lloyd-Lipow model to the data using least squares.
- Plot the reliabilities predicted by the Lloyd-Lipow model along with the observed reliabilities, and compare the results.
| Test Stage Number([math]\displaystyle{ k\,\! }[/math]) | Number of Tests in Stage([math]\displaystyle{ n_k\,\! }[/math]) | Number of Successful Tests([math]\displaystyle{ S_k\,\! }[/math]) | Raw Data Reliability | Lloyd-Lipow Reliability |
|---|---|---|---|---|
| 1 | 9 | 6 | 0.667 | 0.7002 |
| 2 | 9 | 5 | 0.556 | 0.7369 |
| 3 | 8 | 7 | 0.875 | 0.7552 |
| 4 | 10 | 6 | 0.600 | 0.7662 |
| 5 | 9 | 7 | 0.778 | 0.7736 |
| 6 | 10 | 8 | 0.800 | 0.7788 |
| 7 | 10 | 7 | 0.700 | 0.7827 |
| 8 | 10 | 6 | 0.600 | 0.7858 |
| 9 | 11 | 7 | 0.636 | 0.7882 |
| 10 | 11 | 9 | 0.818 | 0.7902 |
| 11 | 9 | 9 | 1.000 | 0.7919 |
| 12 | 12 | 10 | 0.833 | 0.7933 |
| 13 | 12 | 9 | 0.750 | 0.7945 |
| 14 | 11 | 8 | 0.727 | 0.7956 |
| 15 | 10 | 7 | 0.700 | 0.7965 |
| 16 | 10 | 8 | 0.800 | 0.7973 |
| 17 | 11 | 10 | 0.909 | 0.7980 |
| 18 | 10 | 9 | 0.900 | 0.7987 |
| 19 | 9 | 8 | 0.889 | 0.7992 |
| 20 | 8 | 7 | 0.875 | 0.7998 |
Solution
- The least squares estimates are:
- [math]\displaystyle{ \begin{align} \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{1}{k}= & \underset{k=1}{\overset{20}{\mathop \sum }}\,\frac{1}{k}=3.5977 \\ \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{1}{{{k}^{2}}}= & \underset{k=1}{\overset{20}{\mathop \sum }}\,\frac{1}{{{k}^{2}}}=1.5962 \\ \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{{{S}_{k}}}{{{n}_{k}}}= & \underset{k=1}{\overset{20}{\mathop \sum }}\,\frac{{{S}_{k}}}{{{n}_{k}}}=15.4131 \end{align}\,\! }[/math]
- [math]\displaystyle{ \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{{{S}_{k}}}{k\cdot {{n}_{k}}}=\underset{k=1}{\overset{20}{\mathop \sum }}\,\frac{{{S}_{k}}}{k\cdot {{n}_{k}}}=2.5632\,\! }[/math]
- [math]\displaystyle{ \begin{align} \text{ }{{\hat{R}}_{\infty }}= &\frac{\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{{{k}^{2}}}\underset{k=1}{\overset{N}{\mathop{\sum }}}\,{{R}_{k}}-\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k}\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{{{R}_{k}}}{k}}{N\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{{{k}^{2}}}-{{\left( \underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k} \right)}^{2}}} \\ = & \frac{(1.5962)(15.413)-(3.5977)(2.5637)}{(20)(1.5962)-{{(3.5977)}^{2}}} \\ = & 0.8104 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \hat{\alpha }= &\frac{\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k}\underset{k=1}{\overset{N}{\mathop{\sum }}}\,{{R}_{k}}-N\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{{{R}_{k}}}{k}}{N\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{{{k}^{2}}}-{{\left( \underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k} \right)}^{2}}}\\ = & \frac{(3.5977)(15.413)-(20)(2.5637)}{(20)(1.5962)-{{(3.5977)}^{2}}} \\ = & 0.2207 \end{align}\,\! }[/math]
- [math]\displaystyle{ {{R}_{k}}=0.8104-\frac{0.2201}{k}\,\! }[/math]
- The reliabilities from the raw data and the reliabilities predicted from the Lloyd-Lipow reliability growth model are given in the last two columns of the table. The figure below shows the plot. Based on the given data, the model cannot do much more than to basically fit a line through the middle of the points.