Median Rank for Multiple Censored Data: Difference between revisions
Kate Racaza (talk | contribs) (Created page with '{{UConstruction}}{{Banner Weibull Reference Examples}}__NOTOC__ This example validates the median rank calculation for multiple censored data. =Data Source= Table 3.1 on page 78 …') |
Kate Racaza (talk | contribs) No edit summary |
||
| Line 41: | Line 41: | ||
|} | |} | ||
=Results from Weibull++ | =Results from Weibull++= | ||
The coordinates of each point in the following plot shows the failure time and the corresponding median rank. | The coordinates of each point in the following plot shows the failure time and the corresponding median rank. | ||
| Line 50: | Line 50: | ||
The differences between the results in Weibull++ and the book are due to the method of calculating the median ranks (MR). In the book, the following approximation method is used. | The differences between the results in Weibull++ and the book are due to the method of calculating the median ranks (MR). In the book, the following approximation method is used. | ||
::<math>MR_{i}\approx \frac{MON_{i}-0.3}{N+0.4}</math> | |||
<math>MR_{i}\approx \frac{MON_{i}-0.3}{N+0.4}</math> | |||
| Line 59: | Line 58: | ||
In Weibull++, the following exact method is used. | In Weibull++, the following exact method is used. | ||
::<math>MR_{i}= \frac{1}{1+\frac{N-MON_{i}+1}{MON_{i}}F_{0.5,m,n}}</math> | |||
<math>MR_{i}= \frac{1}{1+\frac{N-MON_{i}+1}{MON_{i}}F_{0.5,m,n}}</math> | |||
where <math>m=2(N-MON_{i}+1), n=2xMON_{i}\cdot F_{0.5,m,n}\,\!</math> is the 50 percentile of a F distribution with degree of freedom of ''m'' and ''n''. | where <math>m=2(N-MON_{i}+1), n=2xMON_{i}\cdot F_{0.5,m,n}\,\!</math> is the 50 percentile of a F distribution with degree of freedom of ''m'' and ''n''. | ||
Revision as of 20:17, 27 May 2014
| UNDER CONSTRUCTION |
| Please come back later. |
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example validates the median rank calculation for multiple censored data.
Data Source
Table 3.1 on page 78 in book “Reliability & Life Testing Handbook Vol 2” by Dr. Kececioglu, Prentice-Hall, 1994.
Data
| Num. In Stage | State F or S | Time to Failure |
|---|---|---|
| 1 | F | 5100 |
| 1 | S | 9500 |
| 1 | F | 15000 |
| 1 | S | 22000 |
| 1 | F | 40000 |
Result
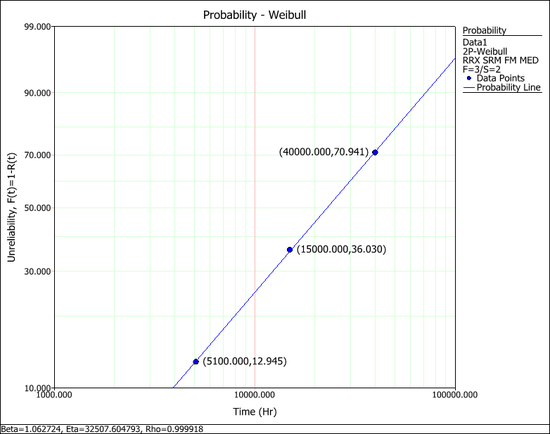
| Num. In Stage | State F or S | Time to Failure | Median Rank (%) |
|---|---|---|---|
| 1 | F | 5100 | 12.94 |
| 1 | S | 9500 | |
| 1 | F | 15000 | 36.1 |
| 1 | S | 22000 | |
| 1 | F | 40000 | 70.84 |
Results from Weibull++
The coordinates of each point in the following plot shows the failure time and the corresponding median rank.
The differences between the results in Weibull++ and the book are due to the method of calculating the median ranks (MR). In the book, the following approximation method is used.
- [math]\displaystyle{ MR_{i}\approx \frac{MON_{i}-0.3}{N+0.4} }[/math]
where [math]\displaystyle{ MR_{i}\,\! }[/math] is the median rank at the [math]\displaystyle{ ith\,\! }[/math] failure time; [math]\displaystyle{ MON_{i}\,\! }[/math] is the mean order number; [math]\displaystyle{ N\,\! }[/math] is the total samples. For the step by step calculation of mean order number (MON), please refer to the book “Reliability & Life Testing Handbook Vol 2” by Dr. Kececioglu, Prentice-Hall, 1994.
In Weibull++, the following exact method is used.
- [math]\displaystyle{ MR_{i}= \frac{1}{1+\frac{N-MON_{i}+1}{MON_{i}}F_{0.5,m,n}} }[/math]
where [math]\displaystyle{ m=2(N-MON_{i}+1), n=2xMON_{i}\cdot F_{0.5,m,n}\,\! }[/math] is the 50 percentile of a F distribution with degree of freedom of m and n.