Sequential Data - Duane Example: Difference between revisions
Kate Racaza (talk | contribs) (Created page with '<noinclude>{{Banner RGA Examples}} ''This example appears in the Reliability Growth and Repairable System Analysis Reference book''. </noinclude> Given the seque…') |
mNo edit summary |
||
| Line 5: | Line 5: | ||
Given the sequential success/failure data in the table below, do the following: | Given the sequential success/failure data in the table below, do the following: | ||
1) Estimate the Duane parameters. | |||
2) What is the instantaneous Reliability at the end of the test? | |||
3) How many additional test runs with a one-sided 90% confidence level are required to meet an instantaneous Reliability goal of 80%? | |||
{|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | {|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | ||
| Line 57: | Line 59: | ||
'''Solution''' | '''Solution''' | ||
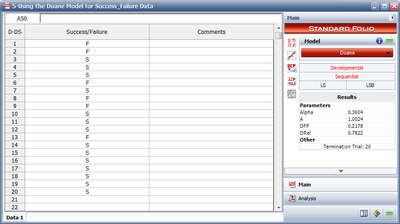
1) The following figure shows the data set entered into RGA along with the estimated Duane parameters. | |||
[[Image:rga4.19.png|thumb|center|400px|Entered data and the estimated parameters.]] | [[Image:rga4.19.png|thumb|center|400px|Entered data and the estimated parameters.]] | ||
2) The Reliability at the end of the test is equal to 78.22%. Note that this is the DRel that is shown in the control panel in the above figure. | |||
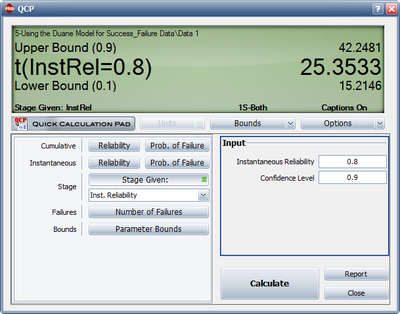
3) The figure below shows the number of test runs with both one-sided confidence bounds at 90% confidence level to achieve an instantaneous Reliability of 80%. Therefore, the number of additional test runs required with a 90% confidence level is equal to <math>42.2481-20=22.2481\approx 23\,\!</math> test runs. | |||
[[Image:rga4.20.png|center|400px|Number of test runs with a one-sided 90% confidence level required to meet an instantaneous MTBF goal of 5 hours.]] | [[Image:rga4.20.png|center|400px|Number of test runs with a one-sided 90% confidence level required to meet an instantaneous MTBF goal of 5 hours.]] | ||
Revision as of 22:57, 30 January 2014
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability Growth and Repairable System Analysis Reference book.
Given the sequential success/failure data in the table below, do the following:
1) Estimate the Duane parameters.
2) What is the instantaneous Reliability at the end of the test?
3) How many additional test runs with a one-sided 90% confidence level are required to meet an instantaneous Reliability goal of 80%?
| Run Number | Result |
|---|---|
| 1 | F |
| 2 | F |
| 3 | S |
| 4 | S |
| 5 | S |
| 6 | F |
| 7 | S |
| 8 | F |
| 9 | F |
| 10 | S |
| 11 | S |
| 12 | S |
| 13 | F |
| 14 | S |
| 15 | S |
| 16 | S |
| 17 | S |
| 18 | S |
| 19 | S |
| 20 | S |
Solution
1) The following figure shows the data set entered into RGA along with the estimated Duane parameters.
2) The Reliability at the end of the test is equal to 78.22%. Note that this is the DRel that is shown in the control panel in the above figure.
3) The figure below shows the number of test runs with both one-sided confidence bounds at 90% confidence level to achieve an instantaneous Reliability of 80%. Therefore, the number of additional test runs required with a 90% confidence level is equal to [math]\displaystyle{ 42.2481-20=22.2481\approx 23\,\! }[/math] test runs.