Crow-AMSAA Discrete Model Grouped Data Example: Difference between revisions
Chris Kahn (talk | contribs) No edit summary |
mNo edit summary |
||
| Line 36: | Line 36: | ||
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows: | Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows: | ||
:<math>\widehat{\beta }=0.7950\,\!</math> | |||
:and: | :and: | ||
:<math>\widehat{\lambda }=0.5588\,\!</math> | |||
As we have seen, the Crow-AMSAA instantaneous failure intensity, <math>{{\lambda }_{i}}(T)\,\!</math>, is defined as: | As we have seen, the Crow-AMSAA instantaneous failure intensity, <math>{{\lambda }_{i}}(T)\,\!</math>, is defined as: | ||
:<math>\begin{align} | |||
{{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T>0,\text{ }\lambda >0\text{ and }\beta >0 | {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T>0,\text{ }\lambda >0\text{ and }\beta >0 | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
Using the parameter estimates, we can calculate the instantaneous unreliability at the end of the test, or <math>T=68.\,\!</math> | Using the parameter estimates, we can calculate the instantaneous unreliability at the end of the test, or <math>T=68.\,\!</math> | ||
:<math>{{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871\,\!</math> | |||
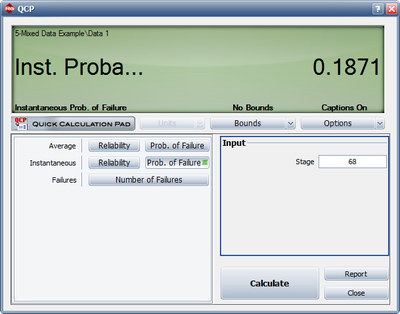
This result that can be obtained from the Quick Calculation Pad (QCP), for <math>T=68,\,\!</math> as seen in the following picture. | This result that can be obtained from the Quick Calculation Pad (QCP), for <math>T=68,\,\!</math> as seen in the following picture. | ||
| Line 61: | Line 58: | ||
The instantaneous reliability can then be calculated as: | The instantaneous reliability can then be calculated as: | ||
:<math>\begin{align} | |||
{{R}_{inst}}=1-0.1871=0.8129 | {{R}_{inst}}=1-0.1871=0.8129 | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
The average unreliability is calculated as: | The average unreliability is calculated as: | ||
:<math>\text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}}\,\!</math> | |||
and the average reliability is calculated as: | and the average reliability is calculated as: | ||
:<math>\text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}}\,\!</math> | |||
Revision as of 17:43, 27 January 2014
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability Growth and Repairable System Analysis Reference book.
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950\,\! }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588\,\! }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T)\,\! }[/math], is defined as:
- [math]\displaystyle{ \begin{align} {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 \end{align}\,\! }[/math]
Using the parameter estimates, we can calculate the instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68.\,\! }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871\,\! }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68,\,\! }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ \begin{align} {{R}_{inst}}=1-0.1871=0.8129 \end{align}\,\! }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}}\,\! }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}}\,\! }[/math]