Logistic Model Examples

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.

---

This example appears in the Reliability Growth and Repairable System Analysis Reference book.

Parameter Estimation: Reliability Data

Using the reliability growth data given in the table below, do the following:

1. Find a Gompertz curve that represents the data and plot it with the raw data.
2. Find a Logistic reliability growth curve that represents the data and plot it with the raw data.

Development Time vs. Observed Reliability data and Predicted Reliabilities

Time, months	Raw Data Reliability (%)	Gompertz Reliability (%)	Logistic Reliablity (%)
0	31.00	24.85	22.73
1	35.50	38.48	38.14
2	49.30	51.95	56.37
3	70.10	63.82	73.02
4	83.00	73.49	85.01
5	92.20	80.95	92.24
6	96.40	86.51	96.14
7	98.60	90.54	98.12
8	99.00	93.41	99.09

Solution

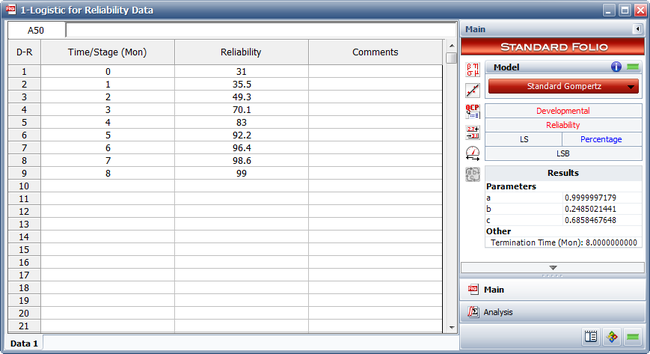
1. The figure below shows the entered data and the estimated parameters using the standard Gompertz model.
   

   Therefore:

   [math]\displaystyle{ \begin{align} & \widehat{a}= & 0.9999 \\ & \widehat{b}= & 0.2485 \\ & \widehat{c}= & 0.6858 \end{align}\,\! }[/math]

   [math]\displaystyle{ R=(0.9999){{(0.2485)}^{{{0.6858}^{T}}}}\,\! }[/math]

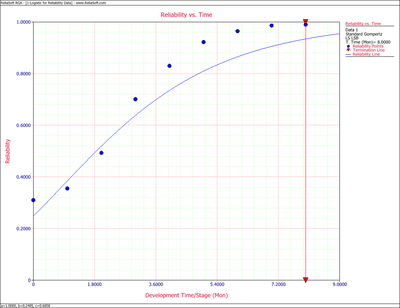
   The values of the predicted reliabilities are plotted in the figure below.

   

   Notice how the standard Gompertz model is not really capable of handling the S-shaped characteristics of this data.

2. The least squares estimators of the Logistic growth curve parameters are given by Crow [9]: where:

   [math]\displaystyle{ \begin{align} {{{\hat{b}}}_{1}}= & \frac{\underset{i=0}{\overset{N-1}{\mathop{\sum }}}\,{{T}_{i}}{{Y}_{i}}-N\cdot \bar{T}\cdot \bar{Y}}{\underset{i=0}{\overset{N-1}{\mathop{\sum }}}\,T_{i}^{2}-N\cdot {{{\bar{T}}}^{2}}} \\ \\ {{{\hat{b}}}_{0}}= & \bar{Y}-{{{\hat{b}}}_{1}}\bar{T} \\ \\ {{Y}_{i}}= & \ln \left( \frac{1}{{{R}_{i}}}-1 \right) \\ \\ \bar{Y}= & \frac{1}{N}\underset{i=0}{\overset{N-1}{\mathop \sum }}\,{{Y}_{i}} \end{align}\,\! }[/math]

   In this example [math]\displaystyle{ N=9\,\! }[/math], which gives:

   [math]\displaystyle{ \begin{align} \overline{Y}&=\frac{1}{9}\sum_{i=0}^{8}ln\left (\frac{1}{R_{i}}-1 \right ) \\ &= -1.7355 \\ \\ \overline{T}&=\frac{1}{9}\sum_{i=0}^{8}T_{i} = 4 \\ \sum_{i=0}^{8}T_{i}^{2} &= 204 \\ \sum_{i=0}^{8}T_{i}Y_{i} &= -106.8630 \end{align}\,\! }[/math]

   From the equations for [math]\displaystyle{ b_{i}\,\! }[/math] and [math]\displaystyle{ \hat{b_{0}}\,\! }[/math]:

   [math]\displaystyle{ \begin{align} \hat{b_{1}} &= \frac{-106.8630 - 9(4)(-1.7355)}{204-9(4)_{2}} \\ & = 0.7398 \\ \hat{b_{0}} &= -1.7355 - (-0.7398)(4)\\ &= 1.2235 \end{align}\,\! }[/math]

   And from the least squares estimators for [math]\displaystyle{ \hat{b}\,\! }[/math] and [math]\displaystyle{ \hat{k}\,\! }[/math]:

   [math]\displaystyle{ \begin{align} \widehat{b}= & {{e}^{1.2235}} \\ = & 3.3991 \\ \widehat{k}= & -(-0.7398) \\ = & 0.7398 \end{align}\,\! }[/math]

   Therefore, the Logistic reliability growth curve that represents this data set is given by:

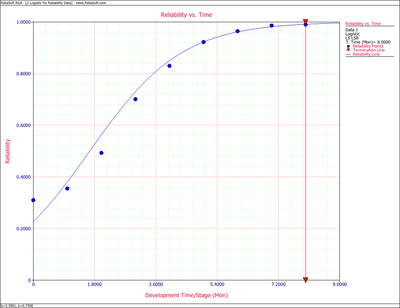
   [math]\displaystyle{ R=\frac{1}{1+3.3991\,{{e}^{-0.7398\,T}}}\,\! }[/math]

   The following figure shows the Reliability vs. Time plot. The plot shows that the observed data set is estimated well by the Logistic reliability growth curve, except in the region closely surrounding the inflection point of the observed reliability. This problem can be overcome by using the modified Gompertz model.
   

Parameter Estimation: Sequential Success/Failure Data

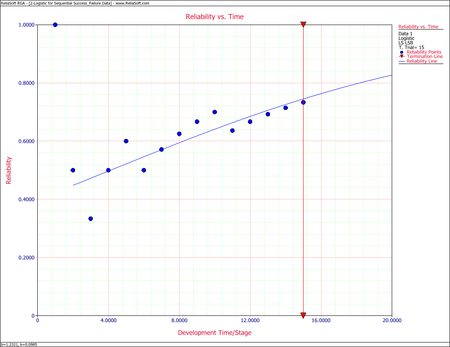
A prototype was tested under a success/failure pattern. The test consisted of 15 runs. The following table presents the data from the test. Find the Logistic model that best fits the data set, and plot it along with the reliability observed from the raw data.

Sequential Success/Failure Data with Observed Reliability Values

Time	Result	Observed Reliability
0	F	0.5000
1	F	0.3333
2	S	0.5000
3	S	0.6000
4	F	0.5000
5	S	0.5714
6	S	0.6250
7	S	0.6667
8	S	0.7000
9	F	0.6364
10	S	0.6667
11	S	0.6923
12	S	0.7143
13	S	0.7333

Solution

The first run is ignored because it was a success, and the reliability at that point was 100%. This failure will be ignored throughout the analysis because it is considered that the test starts when the reliability is not equal to zero or one. The test essentially begins at time 1, and is now considered as time 0 with [math]\displaystyle{ N=14\,\! }[/math]. The observed reliability is shown in the last column of the table. Keep in mind that the observed reliability values still account for the initial suspension.

Therefore:

[math]\displaystyle{ \begin{align} \bar{Y}= & \frac{1}{N}\underset{i=0}{\overset{N-1}{\mathop \sum }}\,{{Y}_{i}} \\ = & \frac{1}{14}\underset{i=0}{\overset{13}{\mathop \sum }}\,\ln \left( \frac{1}{{{R}_{i}}}-1 \right) \\ = & -0.43163 \end{align}\,\! }[/math]

and:

[math]\displaystyle{ \begin{align} \bar{T}= & \frac{1}{14}\underset{i=0}{\overset{13}{\mathop \sum }}\,{{T}_{i}} \\ = & 6.5 \\ \underset{i=0}{\overset{13}{\mathop \sum }}\,T_{i}^{2}= & 819.0 \\ \underset{i=0}{\overset{13}{\mathop \sum }}\,{{T}_{i}}{{Y}_{i}}= & -61.69 \end{align}\,\! }[/math]

Now, from the least squares estimators, the values are:

[math]\displaystyle{ \begin{align} {{{\hat{b}}}_{1}}&= \frac{\underset{i=0}{\overset{N-1}{\mathop{\sum }}}\,{{T}_{i}}{{Y}_{i}}-N\cdot \bar{T}\cdot \bar{Y}}{\underset{i=0}{\overset{N-1}{\mathop{\sum }}}\,T_{i}^{2}-N\cdot {{{\bar{T}}}^{2}}} \\ \\ &= \frac{-61.69-14 \cdot 6.5 \cdot (-.43163)}{819.0-14 \cdot 6.5^{2}} \\ &= -0.0985 \\ \\ \hat{b_{0}}&= \overline{Y} - \hat{b_{1}}\overline{T} \\ &= (-.043163)-(-0.0985) \cdot 6.5 \\ &= 0.2087 \end{align}\,\! }[/math]

Therefore:

[math]\displaystyle{ \begin{align} \widehat{b}= & {{e}^{0.2087}} \\ = & 1.2321 \\ \widehat{k}= & -(-0.0985) \\ = & 0.0985 \end{align}\,\! }[/math]

The Logistic reliability model that best fits the data is given by:

[math]\displaystyle{ R=\frac{1}{1+1.2321\cdot \ \,{{e}^{-0.0985T}}}\,\! }[/math]

The following figure shows the Reliability vs. Time plot.

Parameter Estimation: Grouped per Configuration Data

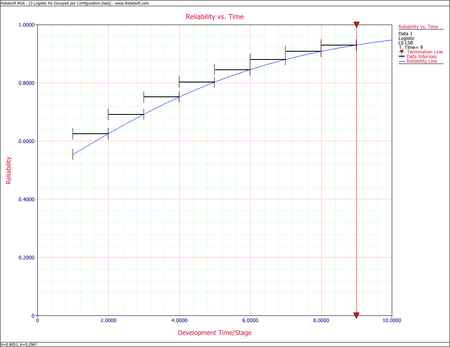
Some equipment underwent testing in different stages. The testing may have been performed in subsequent days, weeks or months with an unequal number of units tested every day. Each group was tested and several failures occurred. The data set is given in columns 1 and 2 of the following table. Find the Logistic model that best fits the data, and plot it along with the reliability observed from the raw data.

Grouped per Configuration Data

Number of Units	Number of Failures	[math]\displaystyle{ T_i\,\! }[/math]	Observed Reliability
10	5	0	0.5000
8	3	1	0.6250
9	3	2	0.6667
9	2	3	0.7778
10	2	4	0.8000
10	1	5	0.9000
10	1	6	0.9000
10	1	7	0.9000
10	1	8	0.9000

Solution

The observed reliability is [math]\displaystyle{ 1-\tfrac{\#\text{ of failures}}{\#\text{ of units}}\,\! }[/math] and the last column of the table above shows the values for each group. With [math]\displaystyle{ N=9\,\! }[/math], the least square estimator [math]\displaystyle{ \overline{Y} }[/math] becomes:

[math]\displaystyle{ \begin{align} \bar{Y}= & \frac{1}{9}\underset{i=0}{\overset{8}{\mathop \sum }}\,\ln \left( \frac{1}{{{R}_{i}}}-1 \right) \\ = & -1.4036 \end{align}\,\! }[/math]

and:

[math]\displaystyle{ \begin{align} \bar{T}= & \frac{1}{9}\underset{i=0}{\overset{8}{\mathop \sum }}\,{{T}_{i}} \\ = & 4 \\ \underset{i=0}{\overset{8}{\mathop \sum }}\,T_{i}^{2}= & 204 \\ \underset{i=0}{\overset{8}{\mathop \sum }}\,{{T}_{i}}{{Y}_{i}}= & -68.33 \end{align}\,\! }[/math]

Now from the least squares estimators, [math]\displaystyle{ \hat{b_{i}}\,\! }[/math] and [math]\displaystyle{ \hat{b_{0}}\,\! }[/math], we have:

[math]\displaystyle{ \begin{align} {{{\hat{b}}}_{1}}= & \frac{\underset{i=0}{\overset{8}{\mathop{\sum }}}\,{{T}_{i}}{{Y}_{i}}-N\cdot \bar{T}\cdot \bar{Y}}{\underset{i=0}{\overset{8}{\mathop{\sum }}}\,T_{i}^{2}-N\cdot {{{\bar{T}}}^{2}}} \\ = & \frac{-68.33-9\cdot 4\cdot \left( -1.4036 \right)}{204-9\cdot {{4}^{2}}} \\ = & -0.2967 \\ & \\ {{{\hat{b}}}_{0}}= & \bar{Y}-{{{\hat{b}}}_{1}}\bar{T} \\ = & \left( -1.4036 \right)-\left( -0.2967 \right)\cdot 4.0 \\ = & -0.2168 \end{align}\,\! }[/math]

Therefore:

[math]\displaystyle{ \begin{align} \widehat{b}= & {{e}^{-0.2168}} \\ = & 0.8051 \\ \widehat{k}= & -(-0.2967) \\ = & 0.2967 \end{align}\,\! }[/math]

The Logistic reliability model that best fits the data is given by:

[math]\displaystyle{ R=\frac{1}{1+0.8051\cdot \ \,{{e}^{-0.2967T}}}\,\! }[/math]

The figure below shows the Reliability vs. Time plot.

Confidence Bounds Example

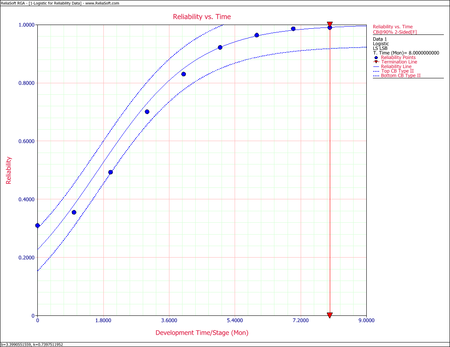
For the data given above for the reliability data example, calculate the 2-sided 90% confidence bounds under the Logistic model for the following:

1. The parameters [math]\displaystyle{ b\,\! }[/math] and [math]\displaystyle{ k\,\! }[/math].
2. Reliability at month 5.

Solution

1. The values of [math]\displaystyle{ \hat{b}\,\! }[/math] and [math]\displaystyle{ \hat{k}\,\! }[/math] that were estimated from the least squares analysis in the reliability data example are:

   [math]\displaystyle{ \begin{align} \widehat{b}= & 3.3991 \\ \widehat{\alpha }= & 0.7398 \end{align}\,\! }[/math]

   Thus, the 2-sided 90% confidence bounds on parameter [math]\displaystyle{ b\,\! }[/math] are:

   [math]\displaystyle{ \begin{align} {{b}_{lower}}= & 2.5547 \\ {{b}_{upper}}= & 4.5225 \end{align}\,\! }[/math]

   The 2-sided 90% confidence bounds on parameter [math]\displaystyle{ k\,\! }[/math] are:

   [math]\displaystyle{ \begin{align} {{k}_{lower}}= & 0.6798 \\ {{k}_{upper}}= & 0.7997 \end{align}\,\! }[/math]

2. First, calculate the reliability estimation at month 5:

   [math]\displaystyle{ \begin{align} {{R}_{5}}= & \frac{1}{1+b{{e}^{-5k}}} \\ = & 0.9224 \end{align}\,\! }[/math]

   Thus, the 2-sided 90% confidence bounds on reliability at month 5 are:

   [math]\displaystyle{ \begin{align} {{[{{R}_{5}}]}_{lower}}= & 0.8493 \\ {{[{{R}_{5}}]}_{upper}}= & 0.9955 \end{align}\,\! }[/math]

   The next figure shows a graph of the reliability plotted with 2-sided 90% confidence bounds.