Highly Fractional Factorial Designs: Difference between revisions
Lisa Hacker (talk | contribs) No edit summary |
No edit summary |
||
| Line 60: | Line 60: | ||
<br> | <br> | ||
====Example==== | |||
<br> | <br> | ||
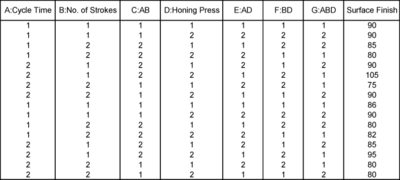
Recall the experiment to investigate factors affecting the surface finish of automobile brake drums discussed in Chapter 7. The three factors investigated in the experiment were honing pressure (factor <math>A</math> ), number of strokes (factor <math>B</math> ) and cycle time (factor <math>C</math> ). Assume that you used Taguchi's L8 orthogonal array to investigate the three factors instead of the 2 <math>^{3}</math> design that was used in Chapter 7. Based on the discussion in the previous section, the preferred columns for the L8 array are the first, second and fourth columns. Therefore, the three factors should be assigned to these columns. The three factors are assigned to these columns based on Figure TaguchiL8 (c), so that you can easily compare results obtained from the L8 array to the ones included in Chapter 7. Based on this assignment, the L8 array for the two replicates, along with the respective response values, should be as shown in Table 8.3. Note that to run the experiment using the L8 array, you would use only the first, the second and the fourth column to set the three factors. | Recall the experiment to investigate factors affecting the surface finish of automobile brake drums discussed in Chapter 7. The three factors investigated in the experiment were honing pressure (factor <math>A</math> ), number of strokes (factor <math>B</math> ) and cycle time (factor <math>C</math> ). Assume that you used Taguchi's L8 orthogonal array to investigate the three factors instead of the 2 <math>^{3}</math> design that was used in Chapter 7. Based on the discussion in the previous section, the preferred columns for the L8 array are the first, second and fourth columns. Therefore, the three factors should be assigned to these columns. The three factors are assigned to these columns based on Figure TaguchiL8 (c), so that you can easily compare results obtained from the L8 array to the ones included in Chapter 7. Based on this assignment, the L8 array for the two replicates, along with the respective response values, should be as shown in Table 8.3. Note that to run the experiment using the L8 array, you would use only the first, the second and the fourth column to set the three factors. | ||
Revision as of 15:58, 2 October 2012
This chapter discusses factorial designs that are commonly used in designed experiments, but are not necessarily limited to two level factors. These designs are the Plackett-Burman designs and Taguchi's orthogonal arrays.
Plackett-Burman Designs
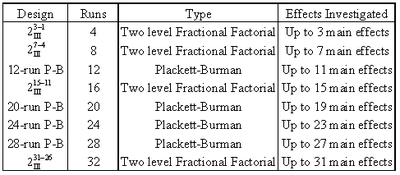
It was mentioned in Chapter 7 that resolution III designs can be used as highly fractional designs to investigate [math]\displaystyle{ k }[/math] main effects using [math]\displaystyle{ k+1 }[/math] runs (provided that three factor and higher order interaction effects are not important to the experimenter). A limitation with these designs is that all runs in these designs have to be a power of 2. The valid runs for these designs are 4, 8, 16, 32, etc. Therefore, the next design after the 2 [math]\displaystyle{ _{\text{III}}^{3-1} }[/math] design with 4 runs is the 2 [math]\displaystyle{ _{\text{III}}^{7-4} }[/math] design with 8 runs, and the design after this is the 2 [math]\displaystyle{ _{\text{III}}^{15-11} }[/math] design with 32 runs and so on (see Table 8.1). Plackett-Burman designs solve this problem. These designs were proposed by R. L. Plackett and J.P. Burman (1946). These designs also allow the estimation of [math]\displaystyle{ k }[/math] main effects using [math]\displaystyle{ k+1 }[/math] runs. In these designs, runs are a multiple of 4. The valid runs for Plackett-Burman designs are 4, 8, 12, 16, 20 and so on. When the runs are a power of 2, these designs correspond to the resolution III two factor fractional factorial designs. Although Plackett-Burman designs are all two level orthogonal designs, the alias structure for these designs is complicated when runs are not a power of 2.
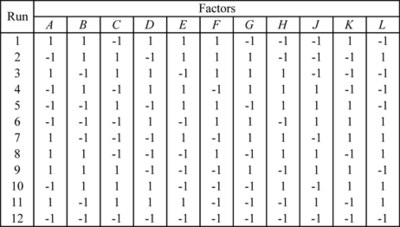
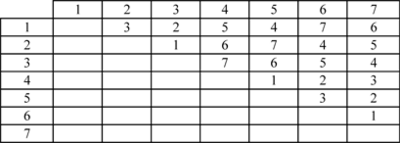
As an example, consider the 12-run Plackett-Burman design shown in Figure PB2runDesign. If 11 main effects are to be estimated using this design, then each of these main effects is partially aliased with all other two factor interactions not containing that main effect. For example, the main effect [math]\displaystyle{ A }[/math] is partially aliased with all two factor interactions except [math]\displaystyle{ AB }[/math] , [math]\displaystyle{ AC }[/math] , [math]\displaystyle{ AD }[/math] , [math]\displaystyle{ AE }[/math] , [math]\displaystyle{ AF }[/math] , [math]\displaystyle{ AG }[/math] , [math]\displaystyle{ AH }[/math] , [math]\displaystyle{ AJ }[/math] , [math]\displaystyle{ AK }[/math] and [math]\displaystyle{ AL }[/math] . There are 45 such two factor interactions that are aliased with [math]\displaystyle{ A }[/math] .
- [math]\displaystyle{ \begin{align} & A= & A-\frac{1}{3}BC-\frac{1}{3}BD+\frac{1}{3}CD-\frac{1}{3}BE-\frac{1}{3}CE+\frac{1}{3}DE+... \\ & & ...+\frac{1}{3}EL-\frac{1}{3}FL-\frac{1}{3}GL+\frac{1}{3}HL+\frac{1}{3}JL-\frac{1}{3}KL \end{align} }[/math]
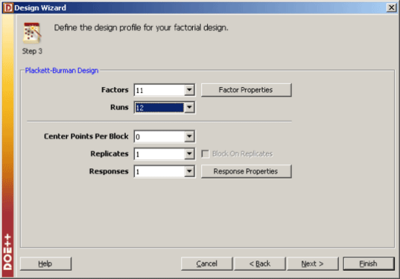
Due to the complex aliasing, Plackett-Burman designs involving a large number of factors should be used with care. Some of the Plackett-Burman designs available in DOE++ are included in Appendix B. The 12-run Plackett-Burman design shown in Figure PB2runDesign can be set up using the properties displayed in Figure PB2runDesignProperties.
[math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math]
Taguchi's Orthogonal Arrays
Taguchi's orthogonal arrays are highly fractional orthogonal designs proposed by Dr. Genichi Taguchi, a Japanese industrialist. These designs can be used to estimate main effects using only a few experimental runs. These designs are not only applicable to two level factorial experiments, but also can investigate main effects when factors have more than two levels. Designs are also available to investigate main effects for certain mixed level experiments where the factors included do not have the same number of levels. As in the case of Placket-Burman designs, these designs require the experimenter to assume that interaction effects are unimportant and can be ignored. A few of Taguchi's orthogonal arrays available in DOE++ are included in Appendix C.
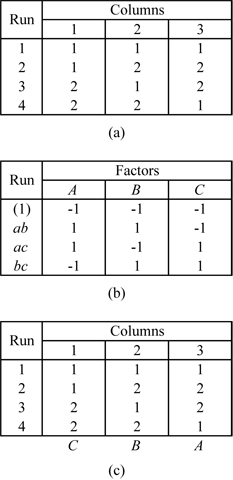
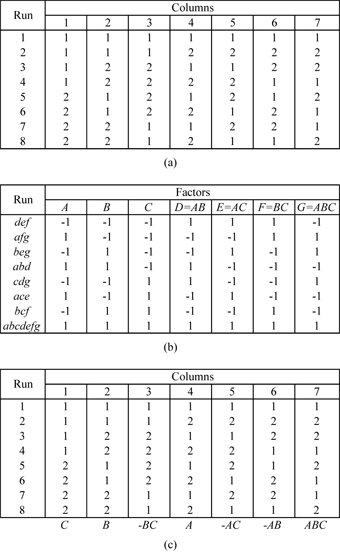
Some of Taguchi's arrays, with runs that are a power of 2, are similar to the corresponding 2 [math]\displaystyle{ _{\text{III}}^{k-f} }[/math] designs. For example, consider the L4 array shown in Figure TaguchiL4 (a). The L4 array is denoted as L4(2^3) in DOE++. L4 means the array requires 4 runs. 2^3 indicates that the design estimates up to three main effects at 2 levels each. The L4 array can be used to estimate three main effects using four runs provided that the two factor and three factor interactions can be ignored. Figure TaguchiL4 (b) shows the 2 [math]\displaystyle{ _{\text{III}}^{3-1} }[/math] design (defining relation [math]\displaystyle{ I=-ABC }[/math] ) which also requires four runs and can be used to estimate three main effects, assuming that all two factor and three factor interactions are unimportant. A comparison between the two designs shows that the columns in the two designs are the same except for the arrangement of the columns. In Figure TaguchiL4 (c), columns of the L4 array are marked with the name of the effect from the corresponding column of the 2 [math]\displaystyle{ _{\text{III}}^{3-1} }[/math] design.
[math]\displaystyle{ }[/math]
Similarly, consider the L8(2^7) array shown in Figure TaguchiL8 (a). This design can be used to estimate seven main effects using eight runs. This array is again similar to the 2 [math]\displaystyle{ _{\text{III}}^{7-4} }[/math] design shown in Figure TaguchiL8 (b), except that the aliasing between the columns of the two designs differs in sign for some of the columns (see Figure TaguchiL8 (c)).
[math]\displaystyle{ }[/math]
The L8 array can also be used as a full factorial three factor experiment design in the same way as a 2 [math]\displaystyle{ ^{3} }[/math] design. However, the orthogonal arrays should be used carefully in such cases, taking into consideration the alias relationships between the columns of the array. For the L8 array, Figure TaguchiL8 (c) shows that the third column of the array is the product of the first two columns. If the L8 array is used as a two level full factorial design in the place of a 2 [math]\displaystyle{ ^{3} }[/math] design, and if the main effects are assigned to the first three columns, the main effect assigned to the third column will be aliased with the two factor interaction of the first two main effects. The proper assignment of the main effects to the columns of the L8 array requires the experimenter to assign the three main effects to the first, second and fourth columns. These columns are sometimes referred to as the preferred columns for the L8 array. To know the preferred columns for any of the orthogonal arrays, the alias relationships between the array columns must be known. The alias relations between the main effects and two factor interactions of the columns for the L8 array are shown in Table 8.2. The cell value in any ( [math]\displaystyle{ i,j }[/math] ) cell of the table gives the column number of the two factor interaction for the [math]\displaystyle{ i }[/math] th and [math]\displaystyle{ j }[/math] th columns. For example, to know which column is confounded with the interaction of the first and second columns, look at the value in the ( [math]\displaystyle{ 1,2 }[/math] ) cell. The value of 3 indicates that the third column is the same as the product of the first and second columns. The alias relations for some of Taguchi's orthogonal arrays are available in Appendix D.
Example
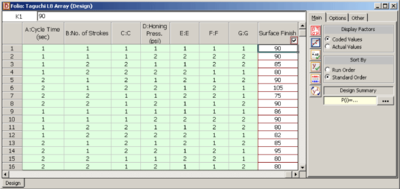
Recall the experiment to investigate factors affecting the surface finish of automobile brake drums discussed in Chapter 7. The three factors investigated in the experiment were honing pressure (factor [math]\displaystyle{ A }[/math] ), number of strokes (factor [math]\displaystyle{ B }[/math] ) and cycle time (factor [math]\displaystyle{ C }[/math] ). Assume that you used Taguchi's L8 orthogonal array to investigate the three factors instead of the 2 [math]\displaystyle{ ^{3} }[/math] design that was used in Chapter 7. Based on the discussion in the previous section, the preferred columns for the L8 array are the first, second and fourth columns. Therefore, the three factors should be assigned to these columns. The three factors are assigned to these columns based on Figure TaguchiL8 (c), so that you can easily compare results obtained from the L8 array to the ones included in Chapter 7. Based on this assignment, the L8 array for the two replicates, along with the respective response values, should be as shown in Table 8.3. Note that to run the experiment using the L8 array, you would use only the first, the second and the fourth column to set the three factors.
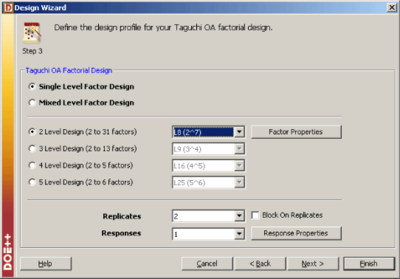
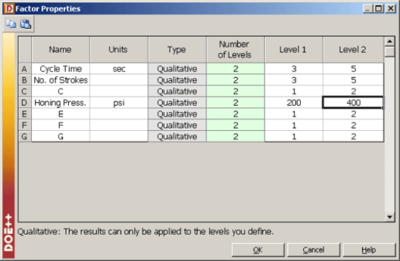
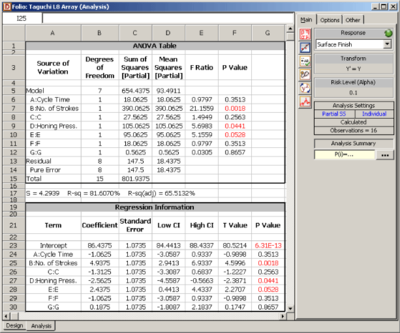
The experiment design for this example can be set using the properties shown in Figure TaguchiL8FactProps. Note that for this design, the factor properties are set up as shown in the design folio using the Factor Properties icon in the Control Panel. The factor properties to be used are shown in Figure TaguchiL8FactProps2. The resulting design along with the response values is shown in Figure TaguchiL8DesignSshot and the results from DOE++ for the design are shown in Figure TaguchiL8Results. The results identify honing pressure, number of strokes, and the interaction between honing pressure and cycle time to be significant effects. This is identical to the conclusion obtained from the 2 [math]\displaystyle{ ^{3} }[/math] design used in Chapter 7. [math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math]