RGA Overview

What is Reliability Growth?

In general, the first prototypes produced during the development of a new complex system will contain design, manufacturing and/or engineering deficiencies. Because of these deficiencies, the initial reliability of the prototypes may be below the system's reliability goal or requirement. In order to identify and correct these deficiencies, the prototypes are often subjected to a rigorous testing program. During testing, problem areas are identified and appropriate corrective actions (or redesigns) are taken. Reliability growth is the improvement in the reliability of a product (component, subsystem or system) over a period of time due to changes in the product's design and/or the manufacturing process. A reliability growth program is a well-structured process of finding reliability problems by testing, incorporating corrective actions and monitoring the increase of the product's reliability throughout the test phases. The term growth is used since it is assumed that the reliability of the product will increase over time as design changes and fixes are implemented. However, in practice, no growth or negative growth may occur.

Reliability goals are generally associated with a reliability growth program. A program may have more than one reliability goal. For example, there may be a reliability goal associated with failures resulting in unscheduled maintenance actions and a separate goal associated with those failures causing a mission abort or catastrophic failure. Other reliability goals may be associated with failure modes that are safety related. The monitoring of the increase of the product's reliability through successive phases in a reliability growth testing program is an important aspect of attaining these goals. Reliability growth analysis (RGA) concerns itself with the quantification and assessment of parameters (or metrics) relating to the product's reliability growth over time. Reliability growth management addresses the attainment of the reliability objectives through planning and controlling of the reliability growth process.

Reliability growth testing can take place at the system, major subsystem or lower unit level. For a comprehensive program, the testing may employ two general approaches: integrated and dedicated. Most development programs have considerable testing that takes place for reasons other than reliability. Integrated reliability growth utilizes this existing testing to uncover reliability problems and incorporate corrective actions. Dedicated reliability growth testing is a test program focused on uncovering reliability problems, incorporating corrective actions and typically, the achievement of a reliability goal. With lower level testing, the primary focus is to improve the reliability of a unit of the system, such as an engine, water pump, etc. Lower level testing, which may be dedicated or integrated, may take place, for example, during the early part of the design phase. Later, the system and subsystem prototypes may be subjected to dedicated reliability growth testing, integrated reliability growth testing or both. Modern applications of reliability growth extend these methods to early design and to in-service customer use. Reliability growth management concerns itself with the planning and management of an item's reliability growth as a function of time and resources.

Reliability growth occurs from corrective and/or preventive actions based on experience gained from failures and from analysis of the equipment, design, production and operation processes. The reliability growth "Test-Analyze-Fix" concept in design is applied by uncovering weaknesses during the testing stages and performing appropriate corrective actions before full-scale production. A corrective action takes place at the problem and root cause level. Therefore, a failure mode is a problem and root cause. Reliability growth addresses failure modes. For example, a problem such as a seal leak may have more than one cause. Each problem and cause constitutes a separate failure mode and, in some cases, requires separate corrective actions. Consequently, there may be several failure modes and design corrections corresponding to a seal leak problem. The formal procedures and manuals associated with the maintenance and support of the product are part of the system design and may require improvement. Reliability growth is due to permanent improvements in the reliability of a product that result from changes in the product design and/or the manufacturing process. Rework, repair and temporary fixes do not constitute reliability growth.

Screening addresses the reliability of an individual unit and not the inherent reliability of the design. If the population of devices is heterogeneous then the high failure rate items are naturally screened out through operational use or testing. Such screening can improve the mixture of a heterogeneous population, generating an apparent growth phenomenon when in fact the devices themselves are not improving. This is not considered reliability growth. Screening is a form of rework. Reliability growth is concerned with permanent corrective actions focused on prevention of problems.

Learning by operator and maintenance personnel also plays an important role in the improvement scenario. Through continued use of the equipment, operator and maintenance personnel become more familiar with it. This is called natural learning. Natural learning is a continuous process that improves reliability as fewer mistakes are made in operation and maintenance, since the equipment is being used more effectively. The learning rate will be increasing in early stages and then level off when familiarity is achieved. Natural learning can generate lessons learned and may be accompanied by revisions of technical manuals or even specialized training for improved operation and maintenance. Reliability improvement due to written and institutionalized formal procedures and manuals that are a permanent implementation to the system design is part of the reliability growth process. Natural learning is an individual characteristic and is not reliability growth.

The concept of reliability growth is not just theoretical or absolute. Reliability growth is related to factors such as the management strategy toward taking corrective actions, effectiveness of the fixes, reliability requirements, the initial reliability level, reliability funding and competitive factors. For example, one management team may take corrective actions for 90% of the failures seen during testing, while another management team with the same design and test information may take corrective actions on only 65% of the failures seen during testing. Different management strategies may attain different reliability values with the same basic design. The effectiveness of the corrective actions is also relative when compared to the initial reliability at the beginning of testing. If corrective actions give a 400% improvement in reliability for equipment that initially had one tenth of the reliability goal, this is not as significant as a 50% improvement in reliability if the system initially had one half the reliability goal.

Why Reliability Growth?

It is typical in the development of a new technology or complex system to have reliability goals. Each goal will generally be associated with a failure definition. The attainment of the various reliability goals usually involves implementing a reliability program and performing reliability tasks. These tasks will vary from program to program. A reference of common reliability tasks is MIL-STD-785B. It is widely used and readily available. Table 2.1 presents the tasks included in MIL-STD 785B.

Table 2.1 - MIL-STD-785B reliability tasks

	Design and Evaluation		Program Surveillance and Control		Development and Production Testing
101	Reliability Program Plan	201	Reliability modeling	301	Environmental Stress Screening (ESS)
102	Monitor/Control of Subcontractors and Suppliers	202	Reliability Allocations	302	Reliability Development/Growth Test(RDGT) Program
103	Program Reviews	203	Reliability Predictions	303	Reliability Qualification Test (RGT) Program
104	Failure Reporting, Analysis and Corrective Action System (FRACAS)	204	Failure Modes, Effects and Criticality Analysis(FMECA)	304	Production Reliability Acceptance Test (PRAT) Program
105	Failure Review Board(FRB)	205	Sneak Circuit Analysis(SCA)
		206	Electronic Parts/Circuit Tolerance Analysis
		207	Parts Program
		208	Reliability Critical Items
		209	Effects of Functional Testing, Storage, Handling, Packaging, Transportation and Maintenance

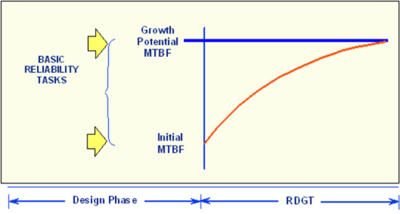
The Program Surveillance and Control tasks (101-105) and Design and Evaluation tasks (201-209) can be combined into a group called basic reliability tasks. These are basic tasks in the sense that many of these tasks are included in a comprehensive reliability program. Of the MIL-STD-785B Development & Production Testing tasks (301-304) only the RDGT reliability growth testing task is specifically directed toward finding and correcting reliability deficiencies.

For discussion purposes, consider the reliability metric mean time between failures (MTBF). This term is used for continuous systems, as well as one shot systems. For one shot systems this metric is the mean trial or shot between failures and is equal to [math]\displaystyle{ \tfrac{1}{failure\text{ }probability} }[/math] .

The MTBF of the prototypes immediately after the basic reliability tasks are completed is called the initial MTBF. This is a key basic reliability task output parameter. If the system is tested after the completion of the basic reliability tasks then the initial MTBF is the mean time between failures as demonstrated from actual data. The initial MTBF is the reliability achieved by the basic reliability tasks and would be the system MTBF if the reliability program were stopped after the basic reliability tasks had been completed.

The initial MTBF after the completion of the basic reliability tasks will generally be lower than the goal. If this is the case then a reliability growth program is appropriate. Formal reliability growth testing is usually conducted after the basic reliability tasks have been completed. For a system subjected to RDGT, the initial MTBF is the system reliability at the beginning of the test. The objective of the testing is to find problems, implement corrective actions and increase the initial reliability. During RDGT, failures are observed and an underlying failure mode is associated with each failure. A failure mode is defined by a problem and a cause. When a new failure mode is observed during testing, management makes a decision not to correct or to correct the failure mode in accordance with the management strategy. Failure modes that are not corrected are called A modes and failure modes that receive a corrective action are called B modes. If the corrective action is effective for a B mode, then the failure intensity for the failure mode will decrease. The effectiveness of the corrective actions is part of the overall management strategy. If the RDGT testing and corrective action process are conducted long enough, the system MTBF will grow to a mature MTBF value in which further corrective actions are very infrequent. This mature MTBF value is called the growth potential. It is a direct function of the design and management strategy. The system growth potential MTBF is the MTBF that would be attained at the end of the basic reliability tasks if all the problem failure modes were uncovered in early design and corrected in accordance with the management strategy.

In summary, the initial MTBF is the value actually achieved by the basic reliability tasks. The growth potential is the MTBF that can be attained if the test is conducted long enough with the current management strategy. See the figure below.

Elements of a Reliability Growth Program

In a formal reliability growth program, one or more reliability goals are set and should be achieved during the development testing program with the necessary allocation or reallocation of resources. Therefore, planning and evaluating are essential factors in a growth process program. A comprehensive reliability growth program needs well-structured planning of the assessment techniques. A reliability growth program differs from a conventional reliability program in that there is a more objectively developed growth standard against which assessment techniques are compared. A comparison between the assessment and the planned value provides a good estimate of whether or not the program is progressing as scheduled. If the program does not progress as planned, then new strategies should be considered. For example, a reexamination of the problem areas may result in changing the management strategy so that more problem failure modes that surface during the testing actually receive a corrective action instead of a repair. Several important factors for an effective reliability growth program are:

• Management: the decisions made regarding the management strategy to correct problems or not correct problems and the effectiveness of the corrective actions

• Testing: provides opportunities to identify the weaknesses and failure modes in the design and manufacturing process

• Failure mode root cause identification: funding, personnel and procedures are provided to analyze, isolate and identify the cause of failures

• Corrective action effectiveness: design resources to implement corrective actions that are effective and support attainment of the reliability goals

• Valid reliability assessments: using valid statistical methodologies to analyze test data in order to assess reliability

The management strategy may be driven by budget and schedule but it is defined by the actual decisions of management in correcting reliability problems. If the reliability of a failure mode is known through analysis or testing, then management makes the decision either not to fix (no corrective action) or to fix (implement a corrective action) that failure mode. Generally, if the reliability of the failure mode meets the expectations of management, then no corrective actions would be expected. If the reliability of the failure mode is below expectations, the management strategy would generally call for the implementation of a corrective action.

Another part of the management strategy is the effectiveness of the corrective actions. A corrective action typically does not eliminate a failure mode from occurring again. It simply reduces its rate of occurrence. A corrective action, or fix, for a problem failure mode typically removes a certain amount of the mode's failure intensity, but a certain amount will remain in the system. The fraction decrease in the problem mode failure intensity due to the corrective action is called the effectiveness factor (EF). The EF will vary from failure mode to failure mode but a typical average for government and industry systems has been reported to be about 0.70. With an EF equal to 0.70, a corrective action for a failure mode removes about 70% of the failure intensity, but 30% remains in the system.

Corrective action implementation raises the following question: "What if some of the fixes cannot be incorporated during testing?" It is possible that only some fixes can be incorporated into the product during testing. However, others may be delayed until the end of the test since it may be too expensive to stop and then restart the test, or the equipment may be too complex for performing a complete teardown. Implementing delayed fixes usually results in a distinct jump in the reliability of the system at the end of the test phase. For corrective actions implemented during testing, the additional follow-on testing provides feedback on how effective the corrective actions are and provides opportunity to uncover additional problems that can be corrected.

Evaluation of the delayed corrective actions is provided by projected reliability values. The demonstrated reliability is based on the actual current system performance and estimates the system reliability due to corrective actions incorporated during testing. The projected reliability is based on the impact of the delayed fixes that will be incorporated at the end of the test or between test phases.

When does a reliability growth program take place in the development process? Actually, there is more than one answer to this question. The modern approach to reliability realizes that typical reliability tasks often do not yield a system that has attained the reliability goals or attained the cost-effective reliability potential in the system. Therefore, reliability growth may start very early in a program, utilizing Integrated Reliability Growth Testing (IRGT). This approach recognizes that reliability problems often surface early in engineering tests. The focus of these engineering tests is typically on performance and not reliability. IRGT simply piggybacks reliability failure reporting, in an informal fashion, on all engineering tests. When a potential reliability problem is observed, reliability engineering is notified and appropriate design action is taken. IRGT will usually be implemented at the same time as the basic reliability tasks. In addition to IRGT, reliability growth may take place during early prototype testing, during dedicated system testing, during production testing, and from feedback through any manufacturing or quality testing or inspections. The formal dedicated testing or RDGT will typically take place after the basic reliability tasks have been completed.

Note that when testing and assessing against a product's specifications, the test environment must be consistent with the specified environmental conditions under which the product specifications are defined. In addition, when testing subsystems it is important to realize that interaction failure modes may not be generated until the subsystems are integrated into the total system.

Why Are Reliability Growth Models Needed?

In order to effectively manage a reliability growth program and attain the reliability goals, it is imperative that valid reliability assessments of the system be available. Assessments of interest generally include estimating the current reliability of the system configuration under test and estimating the projected increase in reliability if proposed corrective actions are incorporated into the system. These and other metrics give management information on what actions to take in order to attain the reliability goals. Reliability growth assessments are made in a dynamic environment where the reliability is changing due to corrective actions. The objective of most reliability growth models is to account for this changing situation in order to estimate the current and future reliability and other metrics of interest. The decision for choosing a particular growth model is typically based on how well it is expected to provide useful information to management and engineering. Reliability growth can be quantified by looking at various metrics of interest such as the increase in the MTBF, the decrease in the failure intensity or the increase in the mission success probability, which are generally mathematically related and can be derived from each other. All key estimates used in reliability growth management such as demonstrated reliability, projected reliability and estimates of the growth potential can generally be expressed in terms of the MTBF, failure intensity or mission reliability. Changes in these values, typically as a function of test time, are collectively called reliability growth trends and are usually presented as reliability growth curves. These curves are often constructed based on certain mathematical and statistical models called reliability growth models. The ability to accurately estimate the demonstrated reliability and calculate projections to some point in the future can help determine the following:

• Whether the stated reliability requirements will be achieved

• The associated time for meeting such requirements

• The associated costs of meeting such requirements

• The correlation of reliability changes with reliability activities

In addition, demonstrated reliability and projections assessments aid in:

• Establishing warranties

• Planning for maintenance resources and logistic activities

• Life-cycle-cost analysis

Reliability Growth Analysis

Reliability growth analysis is the process of collecting, modeling, analyzing and interpreting data from the reliability growth development test program (development testing). In addition, reliability growth models can be applied for data collected from the field (fielded systems). Fielded systems analysis also includes the ability to analyze data of complex repairable systems. Depending on the metric(s) of interest and the data collection method, different models can be utilized (or developed) to analyze the growth processes.

As an example of such a model development, consider the simple case of a wine glass designed to withstand a fall of three feet onto a level cement surface.

The success/failure result of such a drop is determined by whether or not the glass breaks.

Furthermore, assume that:

• You will continue to drop the glass, looking at the results and then adjusting the design after each failure until you are sure that the glass will not break.

• Any redesign effort is either completely successful or it does not change the inherent reliability ([math]\displaystyle{ R\,\! }[/math]). In other words, the reliability is either 1 or [math]\displaystyle{ R\,\! }[/math] , [math]\displaystyle{ 0\lt R\lt 1\,\! }[/math] .

• When testing the product, if a success is encountered on any given trial, no corrective action or redesign is implemented.

• If the trial fails, then you will redesign the product.

• When the product is redesigned, assume that the probability of fixing the product permanently before the next trial is [math]\displaystyle{ \alpha \,\! }[/math] . In other words, the glass may or may not have been fixed.

• Let [math]\displaystyle{ {{P}_{n}}(0)\,\! }[/math] and [math]\displaystyle{ {{P}_{n}}(1)\,\! }[/math] be the probabilities that the glass is unreliable and reliable, respectively, just before the [math]\displaystyle{ {{n}^{th}}\,\! }[/math] trial, and that the glass is in the unreliable state just before the first trial, [math]\displaystyle{ {{P}_{1}}(0)\,\! }[/math] .

Now given the above assumptions, the question of how the glass could be in the unreliable state just before trial [math]\displaystyle{ n\,\! }[/math] can be answered in two mutually exclusive ways:

The first possibility is the probability of a successful trial, [math]\displaystyle{ (1-p)\,\! }[/math] , where [math]\displaystyle{ p\,\! }[/math] is the probability of failure in trial [math]\displaystyle{ n-1\,\! }[/math] , while being in the unreliable state, [math]\displaystyle{ {{P}_{n-1}}(0)\,\! }[/math] , before the [math]\displaystyle{ n-1\,\! }[/math] trial:

[math]\displaystyle{ \begin{align} (1-p){{P}_{n-1}}(0) \end{align} }[/math]

Secondly, the glass could have failed the trial, with probability [math]\displaystyle{ p\,\! }[/math] , when in the unreliable state, [math]\displaystyle{ {{P}_{n-1}}(0)\,\! }[/math] , and having failed the trial, an unsuccessful attempt was made to fix, with probability [math]\displaystyle{ (1-\alpha )\,\! }[/math] :

[math]\displaystyle{ \begin{align} p(1-\alpha ){{P}_{n-1}}(0) \end{align} }[/math]

Therefore, the sum of these two probabilities, or possible events, gives the probability of being unreliable just before trial [math]\displaystyle{ n\,\! }[/math] :

[math]\displaystyle{ \begin{align} {{P}_{n}}(0)=(1-p){{P}_{n-1}}(0)+p(1-\alpha ){{P}_{n-1}}(0) \end{align} }[/math]

or:

[math]\displaystyle{ \begin{align} {{P}_{n}}(0)=(1-p\alpha ){{P}_{n-1}}(0) \end{align} }[/math]

By induction, since [math]\displaystyle{ {{P}_{1}}(0)=1\,\! }[/math] :

[math]\displaystyle{ \begin{align} {{P}_{n}}(0)={{(1-p\alpha )}^{n-1}} \end{align} }[/math]

To determine the probability of being in the reliable state just before trial [math]\displaystyle{ n\,\! }[/math] , the above equation is subtracted from 1, therefore:

[math]\displaystyle{ \begin{align} {{P}_{n}}(1)=1-{{(1-p\alpha )}^{n-1}} \end{align} }[/math]

Define the reliability [math]\displaystyle{ {{R}_{n}}\,\! }[/math] of the glass as the probability of not failing at trial [math]\displaystyle{ n\,\! }[/math] . The probability of not failing at trial [math]\displaystyle{ n\,\! }[/math] is the sum of being reliable just before trial [math]\displaystyle{ n\,\! }[/math] , [math]\displaystyle{ (1-{{(1-p\alpha )}^{n-1}})\,\! }[/math] , and being unreliable just before trial [math]\displaystyle{ n\,\! }[/math] but not failing [math]\displaystyle{ \left( {{(1-p\alpha )}^{n-1}}(1-p) \right)\,\! }[/math] , thus:

[math]\displaystyle{ {{R}_{n}}=\left( 1-{{(1-p\alpha )}^{n-1}} \right)+\left( (1-p){{(1-p\alpha )}^{n-1}} \right) }[/math]

or:

[math]\displaystyle{ {{R}_{n}}=1-{{(1-p\alpha )}^{n-1}}\cdot p }[/math]

Now instead of [math]\displaystyle{ {{P}_{1}}(0)=1\,\! }[/math] , assume that the glass has some initial reliability or that the probability that the glass is in the unreliable state at [math]\displaystyle{ n=1\,\! }[/math] , [math]\displaystyle{ {{P}_{1}}(0)=\beta \,\! }[/math] , then:

[math]\displaystyle{ \begin{align} {{R}_{n}}=1-\beta p{{(1-p\alpha )}^{n-1}} \end{align} }[/math]

When [math]\displaystyle{ \beta \lt 1\,\! }[/math] , the reliability at the [math]\displaystyle{ {{n}^{th}}\,\! }[/math] trial is larger than when it was certain that the device was unreliable at trial [math]\displaystyle{ n=1\,\! }[/math] . A trend of reliability growth is observed in the above equation. Let [math]\displaystyle{ A=\beta p\,\! }[/math] and [math]\displaystyle{ C=ln\left( \tfrac{1}{1-p\alpha } \right)\gt 0\,\! }[/math] , then:

[math]\displaystyle{ \begin{align} {{R}_{n}}=1-A{{e}^{-C(n-1)}} \end{align} }[/math]

This equation is now a model that can be utilized to obtain the reliability (or probability that the glass will not break) after the [math]\displaystyle{ {{n}^{th}}\,\! }[/math] trial. Additional models, their applications and methods of estimating their parameters are presented in the following chapters.

Fielded Systems

When a complex system with new technology is fielded and subjected to a customer use environment, there is often considerable interest in assessing its reliability and other related performance metrics, such as availability. This interest in evaluating the system reliability based on actual customer usage failure data may be motivated by a number of factors. For example, the reliability that is generally measured during development is typically related to the system's inherent reliability capability. This inherent capability may differ from actual use experience because of different operating conditions or environment, different maintenance policies, different levels of experience of maintenance personnel, etc. Although operational tests are conducted for many systems during development, it is generally recognized that in many cases these tests may not yield complete data representative of an actual use environment. Moreover, the testing during development is typically limited by the usual cost and schedule constraints, which prevent obtaining a system's reliability profile over an extended portion of its life. Other interests in measuring the reliability of a fielded system may center on, for example, logistics and maintenance policies, quality and manufacturing issues, burn-in, wearout, mission reliability or warranties.

Most complex systems are repaired, not replaced, when they fail. For example, a complex communication system or a truck would be repaired upon failure, not thrown away and replaced by a new system. A number of books and papers in literature have stressed that the usual non-repairable reliability analysis methodologies, such as the Weibull distribution, are not appropriate for repairable system reliability analyses and have suggested the use of nonhomogeneous Poisson process models instead.

The homogeneous process is equivalent to the widely used Poisson distribution and exponential times between system failures can be modeled appropriately when the system's failure intensity is not affected by the system's age. However, to realistically consider burn-in, wearout, useful life, maintenance policies, warranties, mission reliability, etc., the analyst will often require an approach that recognizes that the failure intensity of these systems may not be constant over the operating life of interest but may change with system age. A useful, and generally practical, extension of the homogeneous Poisson process, is the nonhomogeneous Poisson process, which allows for the system failure intensity to change with system age. Typically, the reliability analysis of a repairable system under customer use will involve data generated by multiple systems. Crow [17] proposed the Weibull process or power law nonhomogeneous Poisson process for this type of analysis and developed appropriate statistical procedures for maximum likelihood estimation, goodness-of-fit and confidence bounds.

Failure Rate and Failure Intensity

Failure rate and failure intensity are very similar terms. The term failure intensity typically refers to a process such as a reliability growth program. The system age when a system is first put into service is time 0. Under the non-homogeneous Poisson process (NHPP), the first failure is governed by a distribution [math]\displaystyle{ F(x)\,\! }[/math] with failure rate [math]\displaystyle{ r(x)\,\! }[/math] . Each succeeding failure is governed by the intensity function [math]\displaystyle{ u(t)\,\! }[/math] of the process. Let [math]\displaystyle{ t\,\! }[/math] be the age of the system and [math]\displaystyle{ \Delta t\,\! }[/math] is very small. The probability that a system of age [math]\displaystyle{ t\,\! }[/math] fails between [math]\displaystyle{ t\,\! }[/math] and [math]\displaystyle{ t+\Delta t\,\! }[/math] is given by the intensity function [math]\displaystyle{ u(t)\Delta t\,\! }[/math] . Notice that this probability is not conditioned on not having any system failures up to time [math]\displaystyle{ t\,\! }[/math] , as is the case for a failure rate. The failure intensity [math]\displaystyle{ u(t)\,\! }[/math] for the NHPP has the same functional form as the failure rate governing the first system failure. Therefore, [math]\displaystyle{ u(t)=r(t)\,\! }[/math] , where [math]\displaystyle{ r(t)\,\! }[/math] is the failure rate for the distribution function of the first system failure. If the first system failure follows the Weibull distribution, the failure rate is:

[math]\displaystyle{ \begin{align} r(x)=\lambda \beta {{x}^{\beta -1}} \end{align} }[/math]

Under minimal repair, the system intensity function is:

[math]\displaystyle{ \begin{align} u(t)=\lambda \beta {{t}^{\beta -1}} \end{align} }[/math]

This is the power law model. It can be viewed as an extension of the Weibull distribution. The Weibull distribution governs the first system failure and the power law model governs each succeeding system failure. Additional information on the power law model can also be found here.