Optimum Replacement Time Example

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at BlockSim examples and BlockSim reference examples.

---

This example appears in the article Preventive Maintenance.

This example demonstrates BlockSim 8's Optimum Replacement utility, which allows you to determine the most cost-effective time to replace one or more blocks in one or more systems, based on their planned and unplanned replacement costs.

Optimum Replacement Time

The failure distribution of a component is described by a 2-parameter Weibull distribution with [math]\displaystyle{ \beta = 2.5\,\! }[/math] and [math]\displaystyle{ \eta = 1000\,\! }[/math] hours.

• The cost for a corrective replacement is $5.
  
• The cost for a preventive replacement is $1.
  

Estimate the optimum replacement age in order to minimize these costs.

Solution

Prior to obtaining an optimum replacement interval for this component, the assumptions of the following equation must be checked.

[math]\displaystyle{ \begin{align} CPUT\left( t \right)= & \frac{\text{Total Expected Replacement Cost per Cycle}}{\text{Expected Cycle Length}} \\ = & \frac{{{C}_{P}}\cdot R\left( t \right)+{{C}_{U}}\cdot \left[ 1-R\left( t \right) \right]}{\mathop{}_{0}^{t}R\left( s \right)ds} \end{align} }[/math]

The component has an increasing failure rate because it follows a Weibull distribution with [math]\displaystyle{ \beta \,\! }[/math] greater than 1. Note that if [math]\displaystyle{ \beta =1\,\! }[/math], then the component has a constant failure rate, but if [math]\displaystyle{ \beta \lt 1\,\! }[/math], then it has a decreasing failure rate. If either of these cases exist, then preventive replacement is unwise. Furthermore, the cost for preventive replacement is less than the corrective replacement cost. Thus, the conditions for the optimum age replacement policy have been met.

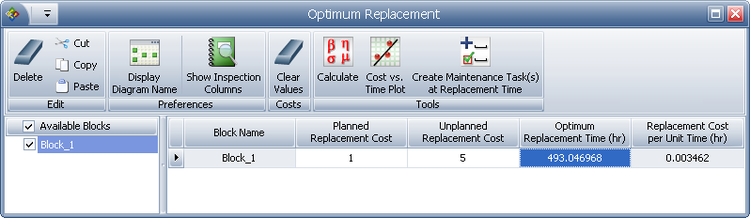
Using BlockSim 8, enter the parameters of the Weibull distribution in the component's Block Properties window. Next, open the Optimum Replacement window and enter the $1 in the Additional Planned Replacement Cost column, and $5 in the Additional Unplanned Replacement Cost column. Click Calculate. In the Optimum Replacement Calculations window that appears, select the Calculate the individual optimum replacement times option and click OK. The optimum replacement time for the component is estimated to be [math]\displaystyle{ 493.0470 }[/math], as shown next.

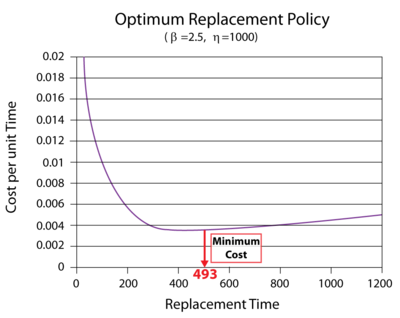
The figure below shows the Cost vs. Time plot of the component (with the scaling adjusted and the plot annotated to show the minimum cost).

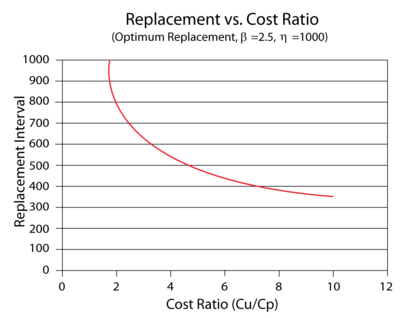
The effect of the corrective/preventive cost ratio on the optimum replacement interval is plotted in the following figure. It can be seen that as the cost ratio increases, the optimum replacement interval decreases. This is an expected result because the corrective replacement costs are much greater than the preventive replacement costs. Therefore, it becomes more cost-effective to replace the component more frequently before it fails.