Template:Testing methodology rga

Testing Methodology

The methodology described here will use the Crow Extended model (presented in Chapter 9) for data analysis. In order to have valid Crow Extended model assessments, it is required that the operational mission profile be conducted in a structured manner. Therefore, this testing methodology involves convergence and stopping points during the testing. A stopping point is when the testing is stopped for the expressed purpose of incorporating the Type BD delayed corrective actions. There may be more than one stopping point during a particular testing phase. For simplicity, the methodology with only one stopping point will be described; however, the methodology can be extended to the case of more than one stopping point. A convergence point is a time during the test when all the operational mission profile tasks meet their expected averages or fall within an acceptable range. At least three convergence points are required for a well-balanced test. The end of the test, time [math]\displaystyle{ T }[/math] , must be a convergence point. The test times between the convergence points do not have to be the same.

The objective of having the convergence points is to be able to apply the Crow Extended model directly in such a way that the projection and other key reliability growth parameters can be estimated in a valid fashion. To do this, the grouped data methodology is applied. Note that the methodology also can be used with the Crow-AMSAA (NHPP) model for a simpler analysis without the ability to estimate projected and growth potential reliability. For the Crow-AMSAA (NHPP) grouped data methodology, refer to Chapter 5, Section 3. For grouped data using the Crow Extended model, refer to Chapter 9, Section 6.

Example

Consider the test-fix-find-test data of Example 2 in Chapter 9, which is shown again in Table 12.1. The total test time for this test is 400 hours. Note that for this example we assume one stopping point at the end of the test for the incorporation of the delayed fixes. Suppose that the data set represents a military system with Task 1 firing a gun, Task 2 moving under environment E1 and Task 3 moving under environment E2. For every hour of operation the operational profile states that the system operates in environment E1 70% of the time and in environment E2 30% of the time. In addition, for each hour of operation the gun must be fired 10 times.

In general, it is difficult to manage an operational test so that these operational profiles are continuously met throughout the test. However, the operational mission profile methodology requires that these conditions be met on average at the convergence points. In practice, this almost always can be done with proper program and test management. The convergence points are set for the testing, often at interim assessment points. The process for controlling the convergence at these points involves monitoring a graph for each of the tasks. 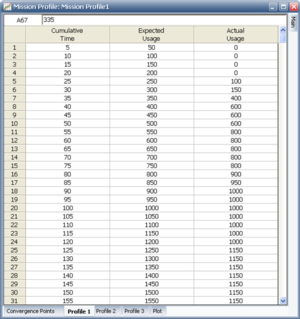Table 12.2 shows the expected and actual results for each of the operational mission profiles.

Table 12.1 - Test-fix-find-test data
[math]\displaystyle{ i }[/math]	[math]\displaystyle{ {{X}_{i}} }[/math]	Mode		[math]\displaystyle{ i }[/math]	[math]\displaystyle{ {{X}_{i}} }[/math]	Mode
1	0.7	BC17		29	192.7	BD11
2	3.7	BC17		30	213	A
3	13.2	BC17		31	244.8	A
4	15	BD1		32	249	BD12
5	17.6	BC18		33	250.8	A
6	25.3	BD2		34	260.1	BD1
7	47.5	BD3		35	263.5	BD8
8	54	BD4		36	273.1	A
9	54.5	BC19		37	274.7	BD6
10	56.4	BD5		38	282.8	BC27
11	63.6	A		39	285	BD13
12	72.2	BD5		40	304	BD9
13	99.2	BC20		41	315.4	BD4
14	99.6	BD6		42	317.1	A
15	100.3	BD7		43	320.6	A
16	102.5	A		44	324.5	BD12
17	112	BD8		45	324.9	BD10
18	112.2	BC21		46	342	BD5
19	120.9	BD2		47	350.2	BD3
20	121.9	BC22		48	355.2	BC28
21	125.5	BD9		49	364.6	BD10
22	133.4	BD10		50	364.9	A
23	151	BC23		51	366.3	BD2
24	163	BC24		52	373	BD8
25	164.7	BD9		53	379.4	BD14
26	174.5	BC25		54	389	BD15
27	177.4	BD10		55	394.9	A
28	191.6	BC26		56	395.2	BD16

Table 12.2 - Expected and actual results for profiles 1, 2, 3
	Profile 1(gun firings)		Profile 2(E1)		Profile 3(E2)
Time	Expected	Actual	Expected	Actual	Expected	Actual
5	50	0	3.5	5	1.5	0
10	100	0	7	10	3	0
15	150	0	10.5	15	4.5	0
20	200	0	14	20	6	0
25	250	100	17.5	25	7.5	0
30	300	150	21	30	9	0
35	350	400	24.5	30	10.5	5
40	400	600	28	30	12	10
45	450	600	31.5	30	13.5	15
50	500	600	35	30	15	20
55	550	800	38.5	35	16.5	20
60	600	800	42	40	18	20
65	650	800	45.5	45	19.5	20
70	700	800	49	50	21	20
75	750	800	52.5	55	22.5	20
80	800	900	56	55	24	25
85	850	950	59.5	55	25.5	30
90	900	1000	63	60	27	30
95	950	1000	66.5	65	28.5	30
100	1000	1000	70	70	30	30
105	1050	1000	73.5	70	31.5	35
...	...	...	...	...	...
...	...	...	...	...	...
355	3550	3440	248.5	259	106.5	96
360	3600	3690	252	264	108	96
365	3650	3690	255.5	269	109.5	96
370	3700	3850	259	274	111	96
375	3750	3850	262.5	279	112.5	96
380	3800	3850	266	280	114	100
385	3850	3850	269.5	280	115.5	105
390	3900	3850	273	280	117	110
395	3950	4000	276.5	280	118.5	115
400	4000	4000	280	280	120	120

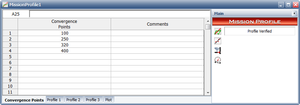
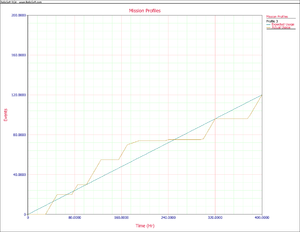
Figure Profile shows a portion of the expected and actual results for mission profile 1, as entered in RGA 7. A graph exists for each of the three tasks in this example. Each graph has a line with the expected average as a function of hours, and the corresponding actual value. When the actual value for a task meets the expected value then is a convergence for that task. A convergence point occurs when all of the tasks converge at the same time. At least three convergence points are required, one of which is the stopping point [math]\displaystyle{ T }[/math] . In our example, the total test time is 400 hours. The convergence points were chosen to be at 100, 250, 320 and 400 hours. Figure convergence points shows the data sheet that contains the convergence points in RGA 7.

[math]\displaystyle{ }[/math]

Entering expected and actual results for profile 1 in RGA 7.

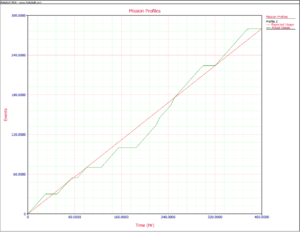
The testing profiles are managed so that at these times the actual operational test profile equals the expected values for the three tasks or falls within an acceptable range. Figure firings shows the expected and actual gun firings. Figure E1 shows the expected and actual time in environment E1 and Figure E2 shows the expected and actual time in environment E2.

[math]\displaystyle{ }[/math]

Specifying convergence points in RGA 7.

Operational mission profile for gun firings.

Operational mission profile for time in environment E1.

Operational mission profile for time in environment E2.

Combined mission profile graph with convergence points.

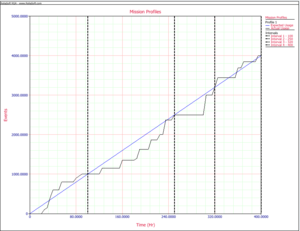
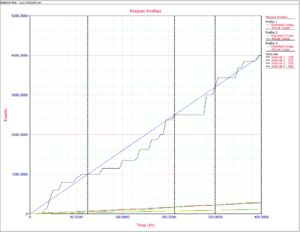
The objective of having the convergence points is to be able to apply the Crow Extended model directly in such a way that the projection and other key reliability growth parameters can be estimated in a valid fashion. To do this, grouped data is applied using the Crow Extended model. For reliability growth assessments using grouped data, only information between time points in the testing is used. In our application, these time points are the convergence points: 100, 250, 320, and 400. Figure Combinedission shows all three mission profiles plotted in the same graph, together with the convergence points.

Table 12.3 gives the grouped data input corresponding to the data in Table 12.1. The parameters of the Crow Extended model for grouped data are then estimated, as explained in Chapter 9, Section 6. Table 12.4 shows the effectiveness factors (EFs) for each of the BD modes.

Table 12.3 - Grouped data at convergence points 100, 250, 320 and 400 hours
Number at Event	Time to Event	Classification	Mode		Number at Event	Time to Event	Classification	Mode
3	100	BC	17		1	250	BC	26
1	100	BD	1		1	250	BD	11
1	100	BC	18		1	250	BD	12
1	100	BD	2		3	320	A
1	100	BD	3		1	320	BD	1
1	100	BD	4		1	320	BD	8
1	100	BC	19		1	320	BD	6
2	100	BD	5		1	320	BC	27
1	100	A			1	320	BD	13
1	100	BC	20		1	320	BD	9
1	100	BD	6		1	320	BD	4
1	250	BD	7		3	400	A
3	250	A			1	400	BD	12
1	250	BD	8		2	400	BD	10
1	250	BC	21		1	400	BD	5
1	250	BD	2		1	400	BD	3
1	250	BC	22		1	400	BC	28
2	250	BD	9		1	400	BD	2
2	250	BD	10		1	400	BD	8
1	250	BC	23		1	400	BD	14
1	250	BC	24		1	400	BD	15
1	250	BC	25		1	400	BD	16

Table 12.4 - Effectiveness Factors for delayed fixes
Mode	Effectiveness Factor
1	0.67
2	0.72
3	0.77
4	0.77
5	0.87
6	0.92
7	0.50
8	0.85
9	0.89
10	0.74
11	0.70
12	0.63
13	0.64
14	0.72
15	0.69
16	0.46

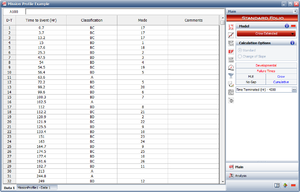
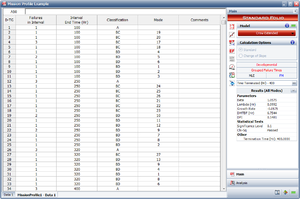
Using the Crow Extended failure times Data Sheet shown in Figure Failure times data, we can analyze this data set based on a mission profile by clicking the mission profile icon:

[math]\displaystyle{ }[/math]

Failure times data.

[math]\displaystyle{ }[/math]

Selecting a mission profile.

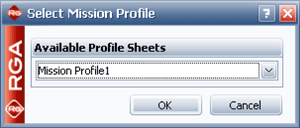
A specific mission profile can then be associated with the Data Sheet, as shown in Figure selecting. This will group the failure times data into groups based on the convergence points that have already been specified when constructing the mission profile.

[math]\displaystyle{ }[/math]

Grouped data set prepared based on the mission profile convergence points.

Instantaneous, demonstrated, projected and growth potential MTBF for grouped data.

A new data sheet with the grouped data is created, as shown in Figure groupedata. The calculated results based on the grouped data are as follows:

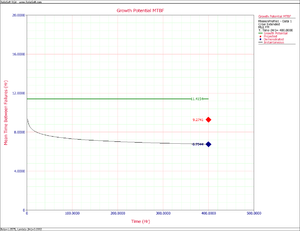
Figure growth potential shows the instantaneous, demonstrated, projected and growth potential MTBF for the grouped data, based the mission profile grouping with intervals at the specified convergence points of the mission profile.