Template:Example: Lognormal Distribution Likelihood Ratio Bound (Reliability): Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
For the data given in [[Lognormal Example 5 Data|Example 5]], determine the two-sided 75% confidence bounds on the reliability estimate for <math>t=65</math> . The ML estimate for the reliability at <math>t=65</math> is 64.261%. | For the data given in [[Lognormal Example 5 Data|Example 5]], determine the two-sided 75% confidence bounds on the reliability estimate for <math>t=65</math> . The ML estimate for the reliability at <math>t=65</math> is 64.261%. | ||
'''Solution''' | '''Solution''' | ||
In this example, we are trying to determine the two-sided 75% confidence bounds on the reliability estimate of 64.261%. This is accomplished by substituting <math>t=65</math> and <math>\alpha =0.75</math> into the likelihood function, and varying <math>{{\sigma'}}</math> until the maximum and minimum values of <math>R</math> are found. The following table gives the values of <math>R</math> based on given values of <math>{{\sigma' }}</math> . | In this example, we are trying to determine the two-sided 75% confidence bounds on the reliability estimate of 64.261%. This is accomplished by substituting <math>t=65</math> and <math>\alpha =0.75</math> into the likelihood function, and varying <math>{{\sigma'}}</math> until the maximum and minimum values of <math>R</math> are found. The following table gives the values of <math>R</math> based on given values of <math>{{\sigma' }}</math> . | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| Line 25: | Line 23: | ||
0.36 & 43.450% & 79.444% & {} & {} & {} \\ | 0.36 & 43.450% & 79.444% & {} & {} & {} \\ | ||
\end{matrix}</math></center> | \end{matrix}</math></center> | ||
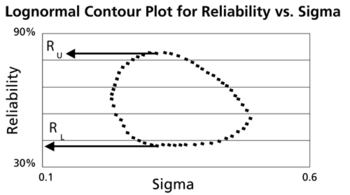
This data set is represented graphically in the following contour plot: | This data set is represented graphically in the following contour plot: | ||
[[Image:WB.10 reliability v sigma.png|center| | [[Image:WB.10 reliability v sigma.png|center|350px| ]] | ||
As can be determined from the table, the lowest calculated value for <math>R</math> is 43.444%, while the highest is 81.508%. These represent the two-sided 75% confidence limits on the reliability at <math>t=65</math> . | As can be determined from the table, the lowest calculated value for <math>R</math> is 43.444%, while the highest is 81.508%. These represent the two-sided 75% confidence limits on the reliability at <math>t=65</math> . | ||
Revision as of 05:02, 8 August 2012
Lognormal Distribution Likelihood Ratio Bound Example (Reliability)
For the data given in Example 5, determine the two-sided 75% confidence bounds on the reliability estimate for [math]\displaystyle{ t=65 }[/math] . The ML estimate for the reliability at [math]\displaystyle{ t=65 }[/math] is 64.261%.
Solution
In this example, we are trying to determine the two-sided 75% confidence bounds on the reliability estimate of 64.261%. This is accomplished by substituting [math]\displaystyle{ t=65 }[/math] and [math]\displaystyle{ \alpha =0.75 }[/math] into the likelihood function, and varying [math]\displaystyle{ {{\sigma'}} }[/math] until the maximum and minimum values of [math]\displaystyle{ R }[/math] are found. The following table gives the values of [math]\displaystyle{ R }[/math] based on given values of [math]\displaystyle{ {{\sigma' }} }[/math] .
This data set is represented graphically in the following contour plot:
As can be determined from the table, the lowest calculated value for [math]\displaystyle{ R }[/math] is 43.444%, while the highest is 81.508%. These represent the two-sided 75% confidence limits on the reliability at [math]\displaystyle{ t=65 }[/math] .