2P Exponential Example: Difference between revisions
Lisa Hacker (talk | contribs) No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
{{Banner Weibull Examples}} | {{Banner Weibull Examples}} | ||
'''2 Parameter Exponential Distribution RRY''' | |||
Fourteen units were being reliability tested and the following life test data were obtained: | Fourteen units were being reliability tested and the following life test data were obtained: | ||
Revision as of 11:54, 17 July 2012
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
2 Parameter Exponential Distribution RRY
Fourteen units were being reliability tested and the following life test data were obtained:
| Table - Life Test Data | |
| Data point index | Time-to-failure |
|---|---|
| 1 | 5 |
| 2 | 10 |
| 3 | 15 |
| 4 | 20 |
| 5 | 25 |
| 6 | 30 |
| 7 | 35 |
| 8 | 40 |
| 9 | 50 |
| 10 | 60 |
| 11 | 70 |
| 12 | 80 |
| 13 | 90 |
| 14 | 100 |
Assuming that the data follow a two-parameter exponential distribution, estimate the parameters and determine the correlation coefficient, [math]\displaystyle{ \rho }[/math], using rank regression on Y.
Solution
Construct the following Table, as shown next.
The median rank values ( [math]\displaystyle{ F({{t}_{i}}) }[/math] ) can be found in rank tables or they can be estimated using the Quick Statistical Reference in Weibull++.
Given the values in the table above, calculate [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math]:
- [math]\displaystyle{ \begin{align} \hat{b}= & \frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}}{{y}_{i}}-(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}})(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}})/14}{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,t_{i}^{2}-{{(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}})}^{2}}/14} \\ \\ \hat{b}= & \frac{-927.4899-(630)(-13.2315)/14}{40,600-{{(630)}^{2}}/14} \end{align} }[/math]
or:
- [math]\displaystyle{ \hat{b}=-0.02711 }[/math]
and:
- [math]\displaystyle{ \hat{a}=\overline{y}-\hat{b}\overline{t}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{t}_{i}}}{N} }[/math]
or:
- [math]\displaystyle{ \hat{a}=\frac{-13.2315}{14}-(-0.02711)\frac{630}{14}=0.2748 }[/math]
Therefore:
- [math]\displaystyle{ \hat{\lambda }=-\hat{b}=-(-0.02711)=0.02711\text{ failures/hour} }[/math]
and:
- [math]\displaystyle{ \hat{\gamma }=\frac{\hat{a}}{\hat{\lambda }}=\frac{0.2748}{0.02711} }[/math]
or:
- [math]\displaystyle{ \hat{\gamma }=10.1365\text{ hours} }[/math]
Then:
- [math]\displaystyle{ f(t)=(0.02711)\cdot {{e}^{-0.02711(T-10.136)}} }[/math]
The correlation coefficient can be estimated using equation for calculating the correlation coefficient:
- [math]\displaystyle{ \hat{\rho }=-0.9679 }[/math]
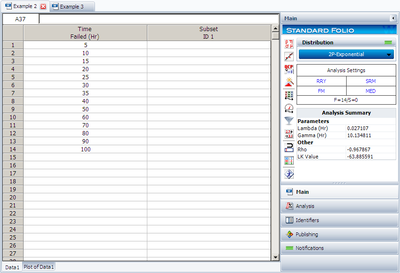
This example can be repeated using Weibull++, choosing two-parameter exponential and rank regression on Y (RRY), as shown in the figure on the following page.
The estimated parameters and the correlation coefficient using Weibull++ were found to be:
- [math]\displaystyle{ \hat{\lambda }=0.0271\text{ fr/hr },\hat{\gamma }=10.1348\text{ hr },\hat{\rho }=-0.9679 }[/math]
Please note that the user must deselect the Reset if Loc. Param > T1 on Exp RR option on the user setup page.
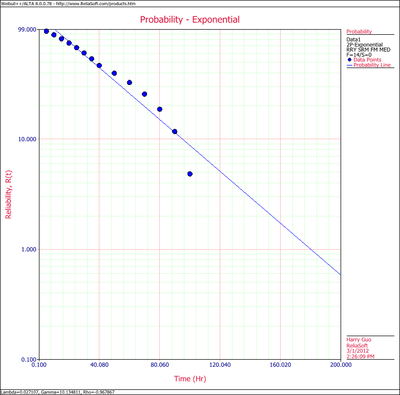
The probability plot can be obtained simply by clicking the Plot icon.