Stress-Strength Analysis in Design for Reliability: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
No edit summary
Line 1: Line 1:
'''Using Stress-Strength Analysis to Determine the Required Strength Distribution'''
'''Using Stress-Strength Analysis to Determine the Required Strength Distribution'''


Assume the stress distribution for a component is known and it is a Weibull distribution with beta=3 and eta=2000. For the current design, the strength distribution is also a Weibull distribution with beta =1.5 and eta=4000.
Assume that the stress distribution for a component is known and it is a Weibull distribution with beta=3 and eta=2000. For the current design, the strength distribution is also a Weibull distribution with beta =1.5 and eta=4000.


: •  Evaluate the current reliability.  
: •  Evaluate the current reliability.  
Line 9: Line 9:
'''Solution'''
'''Solution'''


First, we need to create two empty Weibull++ standard folios and enter the distribution parameters for the stress and strength distributions. For example, for the stress distribution, it is:
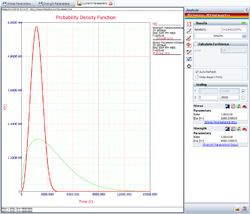
The following picture shows the stress-strength tool and the calculated reliability of the current design. 
 
[[Image: Stress Distribution Example 2.png|thumb|center|250px]]
 
 
Then, we use the Stress-Strength tool to compare the two data sheets. The following figure shows the reliability of the current design:


[[Image: Stress-strength example 2 current reliability.png|thumb|center|250px]]
[[Image: Stress-strength example 2 current reliability.png|thumb|center|250px]]


The above result shows that the current reliability is about 74.05%, which is below the target value of 90%. We need to use the '''Target Reliability Parameter Estimator''' to determine the parameters for the strength distribution that would be required to meet the target. Click the following icon:
The result shows that the current reliability is about 74.05%, which is below the target value of 90%. We need to use the '''Target Reliability Parameter Estimator''' to determine the parameters for the strength distribution that would be required to meet the target.  


[[Image:Stress-strength example 2 target R icon.png|center]]
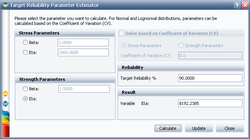
The following picture shows the Target Reliability Parameter Estimator window. In the '''Strength Parameters''' area, select '''eta'''. Set the Target Reliability to '''90%''' and click '''Calculate''':
 
 
Choose to calculate for eta under '''Strength Parameters''', set the Target Reliability to 90% and click '''Calculate''':


[[Image:Stress-strength example 2 Result.png|thumb|center|250px]]
[[Image:Stress-strength example 2 Result.png|thumb|center|250px]]
Line 30: Line 22:
The calculated eta is 8192.2385 hours. Click '''Update''' to perform the stress-strength analysis again using the altered parameters for the strength distribution.
The calculated eta is 8192.2385 hours. Click '''Update''' to perform the stress-strength analysis again using the altered parameters for the strength distribution.


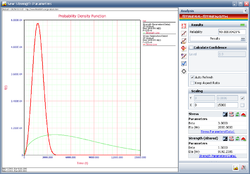
The plot shows the calculated reliability indeed is 90%.  
The following plot shows that the calculated reliability is 90%. Therefore, in order to meet the reliability requirement, the component must be redesigned such that the eta parameter of the strength distribution is at least 8192.2385 hours.


[[Image:Stress-strength example 2 Confirmed Result.png|thumb|center|250px]]
[[Image:Stress-strength example 2 Confirmed Result.png|thumb|center|250px]]
Therefore, in order to meet the reliability requirement, the component must be redesigned with the eta to be at least 8192.2385 hours.

Revision as of 16:24, 30 May 2012

Using Stress-Strength Analysis to Determine the Required Strength Distribution

Assume that the stress distribution for a component is known and it is a Weibull distribution with beta=3 and eta=2000. For the current design, the strength distribution is also a Weibull distribution with beta =1.5 and eta=4000.

• Evaluate the current reliability.
• If the reliability does not meet the target reliability of 90%, determine what parameters would be required for the strength distribution in order to meet the specified target.


Solution

The following picture shows the stress-strength tool and the calculated reliability of the current design.

Stress-strength example 2 current reliability.png

The result shows that the current reliability is about 74.05%, which is below the target value of 90%. We need to use the Target Reliability Parameter Estimator to determine the parameters for the strength distribution that would be required to meet the target.

The following picture shows the Target Reliability Parameter Estimator window. In the Strength Parameters area, select eta. Set the Target Reliability to 90% and click Calculate:

Stress-strength example 2 Result.png


The calculated eta is 8192.2385 hours. Click Update to perform the stress-strength analysis again using the altered parameters for the strength distribution.

The following plot shows that the calculated reliability is 90%. Therefore, in order to meet the reliability requirement, the component must be redesigned such that the eta parameter of the strength distribution is at least 8192.2385 hours.

Stress-strength example 2 Confirmed Result.png
Retrieved from "https://www.reliawiki.com/index.php?title=Stress-Strength_Analysis_in_Design_for_Reliability&oldid=25449"