Eyring Example: Difference between revisions
Jump to navigation
Jump to search
m (moved Eyring-Weibull Example to Eyring Example) |
Chris Kahn (talk | contribs) No edit summary |
||
| Line 26: | Line 26: | ||
<br> | <br> | ||
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of | Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K using: | ||
<br> | <br> | ||
Revision as of 15:24, 22 May 2012
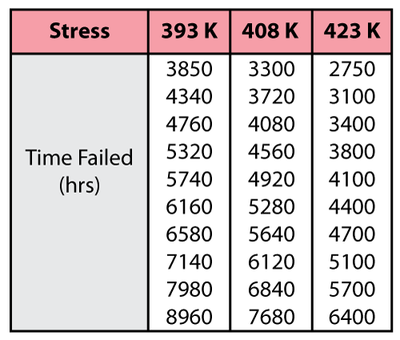
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set using ReliaSoft's ALTA yielding:
- [math]\displaystyle{ \widehat{\beta }=4.29186497 }[/math]
- [math]\displaystyle{ \widehat{A}=-11.08784624 }[/math]
- [math]\displaystyle{ \widehat{B}=1454.08635742 }[/math]
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K using:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right) }[/math]
or:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align} }[/math]