Monte Carlo Simulation Example: Difference between revisions
No edit summary |
No edit summary |
||
| Line 15: | Line 15: | ||
\end{matrix}</math> | \end{matrix}</math> | ||
[[Image:WB.23 lda26.1.png|center| | [[Image:WB.23 lda26.1.png|center|250px| ]] | ||
Determine the number of times (A+B+C) will be greater than D. | Determine the number of times (A+B+C) will be greater than D. | ||
| Line 37: | Line 37: | ||
[[Image:Rsik Analysis Example Monte Carlo Setting.png|thumb|center| | [[Image:Rsik Analysis Example Monte Carlo Setting.png|thumb|center|250px| ]] | ||
[[Image:Rsik Analysis Example Monte Carlo Number of Points.png|thumb|center| | [[Image:Rsik Analysis Example Monte Carlo Number of Points.png|thumb|center|250px| ]] | ||
| Line 44: | Line 44: | ||
[[Image:Rsik Analysis Example Monte Carlo D.png|thumb|center| | [[Image:Rsik Analysis Example Monte Carlo D.png|thumb|center|250px| ]] | ||
| Line 51: | Line 51: | ||
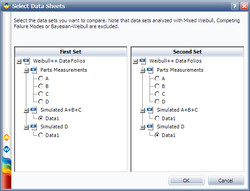
First select the two data sets: | First select the two data sets: | ||
[[Image:Rsik Analysis Example Selected Life Data.png|thumb|center| | [[Image:Rsik Analysis Example Selected Life Data.png|thumb|center|250px| ]] | ||
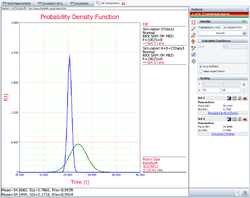
Then calculate them: | Then calculate them: | ||
[[Image:Rsik Analysis Example Selected Life Comparison Plot.png|thumb|center| | [[Image:Rsik Analysis Example Selected Life Comparison Plot.png|thumb|center|250px| ]] | ||
[[Image:Rsik Analysis Example Selected Life Comparison Result.png|thumb|center| | [[Image:Rsik Analysis Example Selected Life Comparison Result.png|thumb|center|250px| ]] | ||
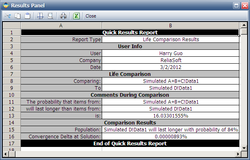
Therefore, the probability that (A+B+C) will be greater than D is <math>100-83.67=16.23%</math> (note that the results could vary because of the randomness in the simulation.) | Therefore, the probability that (A+B+C) will be greater than D is <math>100-83.67=16.23%</math> (note that the results could vary because of the randomness in the simulation.) | ||
Revision as of 23:56, 25 April 2012
Monte Carlo Simulation A Hinge Length Example
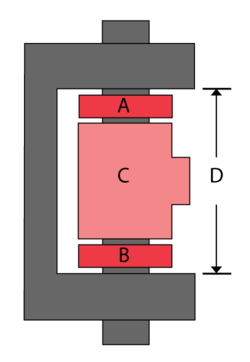
A hinge is made up of four components A, B, C, D. Seven units of each component were taken from the assembly line and the following measurements (in cm) were recorded:
- [math]\displaystyle{ \begin{matrix} \text{Dimensions for A} & \text{Dimensions for B} & \text{Dimensions for C} & \text{Dimensions for D} \\ \text{2}\text{.0187} & \text{1}\text{.9795} & \text{30}\text{.4216} & \text{33}\text{.6573} \\ \text{1}\text{.9996} & \text{2}\text{.0288} & \text{29}\text{.9818} & \text{34}\text{.5432} \\ \text{2}\text{.0167} & \text{1}\text{.9883} & \text{29}\text{.9724} & \text{34}\text{.6218} \\ \text{2}\text{.0329} & \text{2}\text{.0327} & \text{30}\text{.192} & \text{34}\text{.7538} \\ \text{2}\text{.0233} & \text{2}\text{.0119} & \text{29}\text{.9421} & \text{35}\text{.1508} \\ \text{2}\text{.0273} & \text{2}\text{.0354} & \text{30}\text{.1343} & \text{35}\text{.2666} \\ \text{1}\text{.984} & \text{1}\text{.9908} & \text{30}\text{.0423} & \text{35}\text{.7111} \\ \end{matrix} }[/math]
Determine the number of times (A+B+C) will be greater than D.
Solution
The parts dimensions measurements were entered into a Weibull++ standard folio as separate data sheets and were analyzed assuming normal distribution and RRX as the analysis method. The parameters are:
- [math]\displaystyle{ \begin{matrix} \text{A} & \text{B} & \text{C} & \text{D} \\ \hat{\mu }=2.0146 & \hat{\mu }=2.0096 & \hat{\mu }=30.0981 & \hat{\mu }=34.8149 \\ \hat{\sigma }=0.0181 & \hat{\sigma }=0.0249 & \hat{\sigma }=0.1762 & \hat{\sigma }=0.7121 \\ \end{matrix} }[/math]
Based on the above parameters, a Monte Carlo simulation can be performed to estimate the number of times (A+B+C) will be greater than D.
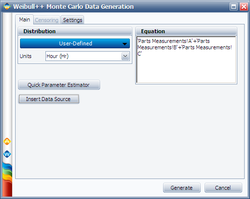
Select Generate Monte Carlo Data...from the Tools menu. Choose User Defined under Distribution and use the Insert Data Source... to use the A, B and C measurements data sheets to generate 100 data points that represent (A+B+C). The new created sheet is then renamed to Simulated A+B+C.
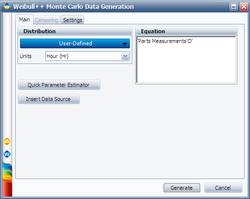
Following the same steps, use the D measurements data sheets to generate 100 data points that represent D. The new created sheet is then renamed to Simulated D.
The two data sets that represent A+B+C and D are modeled with a normal distribution using RRX as the analysis method. Using the Test of Comparison tool, which is under Insert, the two data sets can be compared.
First select the two data sets:
Then calculate them:
Therefore, the probability that (A+B+C) will be greater than D is [math]\displaystyle{ 100-83.67=16.23% }[/math] (note that the results could vary because of the randomness in the simulation.)