Template:Example: Weibull Distribution Interval Data Example: Difference between revisions
Jump to navigation
Jump to search
[math]\displaystyle{ \begin{align}
& \hat{\beta }=5.76 \\
& \hat{\eta }=44.68 \\
\end{align} }[/math]
[math]\displaystyle{ \begin{align}
& \hat{\beta }=5.70 \\
& \hat{\eta }=44.54 \\
\end{align} }[/math]
[math]\displaystyle{ \begin{align}
& \hat{\beta }=5.41 \\
& \hat{\eta }=44.76 \\
\end{align} }[/math]
No edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
Suppose that we have run an experiment with eight units being tested and the following is a table of their last inspection times and times-to-failure: | Suppose that we have run an experiment with eight units being tested and the following is a table of their last inspection times and times-to-failure: | ||
{| border="1" | {| border="1" align="center" | ||
| align="center" style="background:#f0f0f0;"|'''Data Point Index''' | | align="center" style="background:#f0f0f0;"|'''Data Point Index''' | ||
| align="center" style="background:#f0f0f0;"|'''Last Inspection''' | | align="center" style="background:#f0f0f0;"|'''Last Inspection''' | ||
| Line 61: | Line 61: | ||
The plot of the MLE solution with the two-sided 90% confidence bounds is: | The plot of the MLE solution with the two-sided 90% confidence bounds is: | ||
[[Image: MLE Plot.png|thumb|center| | [[Image: MLE Plot.png|thumb|center|250px]] | ||
Revision as of 18:29, 25 April 2012
Weibull Distribution Interval Data Example
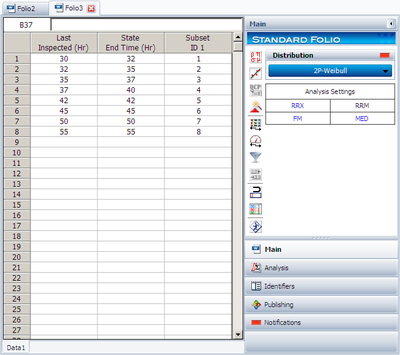
Suppose that we have run an experiment with eight units being tested and the following is a table of their last inspection times and times-to-failure:
| Data Point Index | Last Inspection | Time to Failure |
| 1 | 30 | 32 |
| 2 | 32 | 35 |
| 3 | 35 | 37 |
| 4 | 37 | 40 |
| 5 | 42 | 42 |
| 6 | 45 | 45 |
| 7 | 50 | 50 |
| 8 | 55 | 55 |
Analyze the data using several different parameter estimation techniques and compare the results.
Solution
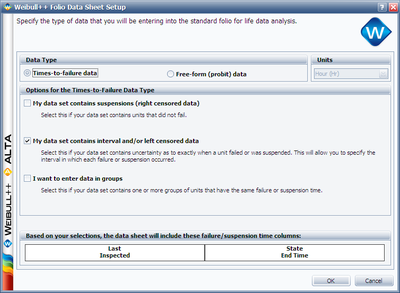
This data set can be entered into Weibull++ by opening a new Data Folio and choosing Times-to-failure and My data set contains interval and/or left censored data.
The data is entered as follows,
The computed parameters using maximum likelihood are:
using RRX or rank regression on X:
and using RRY or rank regression on Y:
The plot of the MLE solution with the two-sided 90% confidence bounds is: