Contour Plot Example: Difference between revisions
Lisa Hacker (talk | contribs) No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
'''Life Comparison - Compare Two Designs Using Contour Plot''' | '''Life Comparison - Compare Two Designs Using Contour Plot''' | ||
The following data | The following data set represents the times-to-failure for a product. Certain modifications were made to this product in order to improve its reliability. Reliability engineers are trying to determine whether the improvements were significant in improving the reliability. | ||
<center><math>\overset{\text{Old Design}}{\mathop{\begin{array}{*{35}{l}} | <center><math>\overset{\text{Old Design}}{\mathop{\begin{array}{*{35}{l}} | ||
| Line 17: | Line 17: | ||
\end{array}}}\,</math> </center> | \end{array}}}\,</math> </center> | ||
At what | At what significance level can the engineers claim that the two designs are different? | ||
'''Solution''' | '''Solution''' | ||
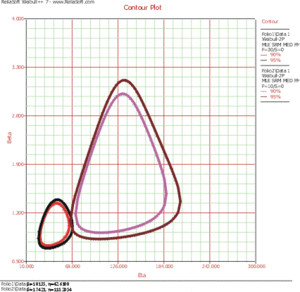
For both data sets the two-parameter Weibull distribution best fits the data. | For both data sets, the two-parameter Weibull distribution best fits the data. The contour plots were generated and plotted together on an overlay plot in Weibull++. | ||
| Line 28: | Line 28: | ||
[[Image:lda24.1.gif|thumb|center|300px| ]] | [[Image:lda24.1.gif|thumb|center|300px| ]] | ||
From this plot, it can be seen that there is an overlap at the 95% confidence level and that there is no overlap at the 90% confidence level. | From this plot, it can be seen that there is an overlap at the 95% confidence level and that there is no overlap at the 90% confidence level. It can then be concluded that the new design is better at the 90% confidence level. If an analyst wanted to know at exactly what confidence the two contour plots meet, she would have to incrementally raise the confidence level from 90% until the two plots met. In fact, this search process has been automated by the Confidence Level Detector utility. | ||
Revision as of 17:57, 30 March 2012
Life Comparison - Compare Two Designs Using Contour Plot
The following data set represents the times-to-failure for a product. Certain modifications were made to this product in order to improve its reliability. Reliability engineers are trying to determine whether the improvements were significant in improving the reliability.
At what significance level can the engineers claim that the two designs are different?
Solution
For both data sets, the two-parameter Weibull distribution best fits the data. The contour plots were generated and plotted together on an overlay plot in Weibull++.
[math]\displaystyle{ }[/math]
From this plot, it can be seen that there is an overlap at the 95% confidence level and that there is no overlap at the 90% confidence level. It can then be concluded that the new design is better at the 90% confidence level. If an analyst wanted to know at exactly what confidence the two contour plots meet, she would have to incrementally raise the confidence level from 90% until the two plots met. In fact, this search process has been automated by the Confidence Level Detector utility.