Template:One parameter exponential distribution example Probability Plot

One Parameter Exponential Probability Plot Example

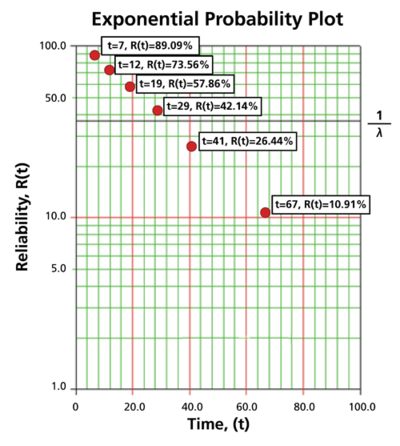
Six units are put on a life test and tested to failure. The failure times are 7, 12, 19, 29, 41, and 67 hours. Estimate the failure rate parameter for a one-parameter exponential distribution using the probability plotting method.

Solution

In order to plot the points for the probability plot, the appropriate reliability estimate values must be obtained. These will be equivalent to [math]\displaystyle{ 100%-MR }[/math], since the y-axis represents the reliability and the [math]\displaystyle{ MR }[/math] values represent unreliability estimates.

[math]\displaystyle{ \begin{matrix} \text{Time-to-} & \text{Reliability} \\ \text{failure, hr} & \text{Estimate, }% \\ 7 & 100-10.91=89.09% \\ 12 & 100-26.44=73.56% \\ 19 & 100-42.14=57.86% \\ 29 & 100-57.86=42.14% \\ 41 & 100-73.56=26.44% \\ 67 & 100-89.09=10.91% \\ \end{matrix} }[/math]

Next, these points are plotted on exponential probability plotting paper. A sample of this type of plotting paper is shown next, with the sample points in place. Notice how these points describe a line with a negative slope. Once the points are plotted, draw the best possible straight line through these points. The time value at which this line intersects with a horizontal line drawn at the 36.8% reliability mark is the mean life, and the reciprocal of this is the failure rate [math]\displaystyle{ \lambda }[/math]. This is because at [math]\displaystyle{ t=m=\tfrac{1}{\lambda } }[/math]:

[math]\displaystyle{ \begin{align} R(t)= & {{e}^{-\lambda \cdot t}} \\ R(t)= & {{e}^{-\lambda \cdot \tfrac{1}{\lambda }}} \\ R(t)= & {{e}^{-1}}=0.368=36.8%. \end{align} }[/math]

These steps are shown graphically in the next pages.

As can be seen in the plot below, the best-fit line through the data points crosses the [math]\displaystyle{ R=36.8% }[/math] line at [math]\displaystyle{ t=33 }[/math] hours.

Since [math]\displaystyle{ \tfrac{1}{\lambda }=33 }[/math] hours, [math]\displaystyle{ \lambda =0.0303 }[/math] failures/hour.