Template:Example: Recurrent Events Data Parameteric Air-Condition Example: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
No edit summary
Line 1: Line 1:
''' Recurrent Events Data Parameteric Air-Condition Example'''
'''Recurrent Events Data Parametric Air-Condition Example'''  
 
The following table gives the failure times of the air-condition unit of an aircraft. The observation is ended by the time of the last failure [[Appendix: Weibull References|[3]]].


The following table gives the failure times of the air-condition unit of an aircraft. The observation ended by the time of the failure occurred. [[Appendix: Weibull References|[3]]]
<center><math>\begin{matrix}
<center><math>\begin{matrix}
   \text{50} & \text{329} & \text{811} & \text{991} & \text{1489}  \\
   \text{50} & \text{329} & \text{811} & \text{991} & \text{1489}  \\
Line 10: Line 9:
   \text{290} & \text{732} & \text{955} & \text{1459} & {}  \\
   \text{290} & \text{732} & \text{955} & \text{1459} & {}  \\
\end{matrix}</math></center>
\end{matrix}</math></center>
:1. Estimate the GRP model parameters using the Type I virtual age option.
:1. Estimate the GRP model parameters using the Type I virtual age option.


Line 19: Line 17:
:4. Using the QCP, calculate the expected failure number and expected instantaneous failure intensity by time 1800.
:4. Using the QCP, calculate the expected failure number and expected instantaneous failure intensity by time 1800.


<br>'''Solution'''


'''Solution'''
Enter the data into a parametric RDA&nbsp;folio in Weibull++. Choose '''3''' under Parameters and '''Type I''' under Settings. Keep the default simulation settings.  
 
Enter the data into a Parametric RDA Specialized Folio in Weibull++. Choose 3 under Parameters and Type I under Settings. Keep the default simulation settings.


:1. The estimated parameters are <math>\hat{\beta }=1.1976,</math>   <math>\hat{\lambda }=4.94E-03,</math>   <math>\hat{q}=0.1344</math> .
:1. The estimated parameters are <math>\hat{\beta }=1.1976,</math> <math>\hat{\lambda }=4.94E-03,</math> <math>\hat{q}=0.1344</math> .


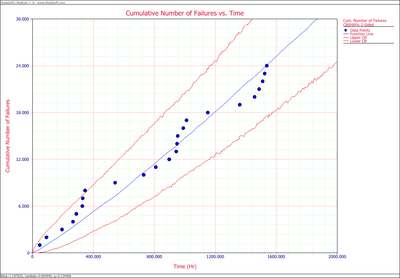
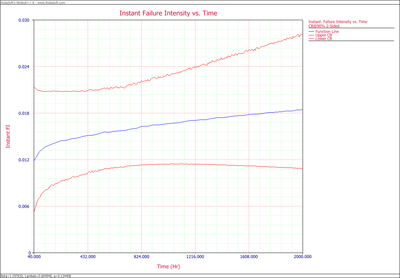
:2. The failure number and instantaneous failure intensity are given in the following plots.
:2. The failure number and instantaneous failure intensity are given in the following plots.


[[Image:Parametric RDA N(T) plot.png|thumb|center|400px| ]]  
[[Image:Parametric RDA N(T) plot.png|thumb|center|400px]]  


[[Image:Parametric RDA Lambda(T) plot.png|thumb|center|400px| ]]  
[[Image:Parametric RDA Lambda(T) plot.png|thumb|center|400px]]  


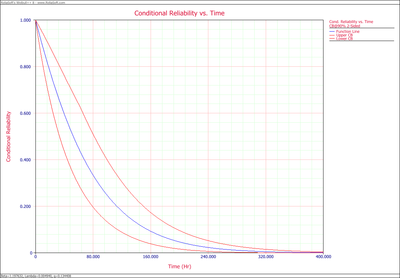
:3. The conditional reliability is plotted below.
:3. The conditional reliability is plotted below.


[[Image:Parametric RDA Cond R(T) plot.png|thumb|center|400px| ]]  
[[Image:Parametric RDA Cond R(T) plot.png|thumb|center|400px]]  


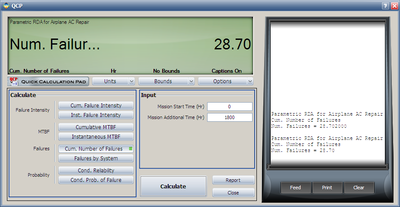
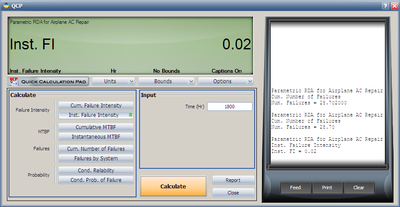
:4. Using QCP, the failure number and instantaneous failure intensity are:
:4. Using QCP, the failure number and instantaneous failure intensity are:


[[Image:QCP N(T).png|thumb|center|400px| ]]  
[[Image:QCP N(T).png|thumb|center|400px]]  


[[Image:QCP Lambda(T).png|thumb|center|400px| ]]
[[Image:QCP Lambda(T).png|thumb|center|400px]]

Revision as of 16:17, 8 March 2012

Recurrent Events Data Parametric Air-Condition Example

The following table gives the failure times of the air-condition unit of an aircraft. The observation ended by the time of the failure occurred. [3]

[math]\displaystyle{ \begin{matrix} \text{50} & \text{329} & \text{811} & \text{991} & \text{1489} \\ \text{94} & \text{332} & \text{899} & \text{1013} & \text{1512} \\ \text{196} & \text{347} & \text{945} & \text{1152} & \text{1525} \\ \text{268} & \text{544} & \text{950} & \text{1362} & \text{1539} \\ \text{290} & \text{732} & \text{955} & \text{1459} & {} \\ \end{matrix} }[/math]
1. Estimate the GRP model parameters using the Type I virtual age option.
2. Plot the failure number and instantaneous failure intensity vs. time with 90% two-sided confidence bounds.
3. Plot the conditional reliability vs. time with 90% two-sided confidence bounds. The mission start time is 40 and mission time is varying.
4. Using the QCP, calculate the expected failure number and expected instantaneous failure intensity by time 1800.


Solution

Enter the data into a parametric RDA folio in Weibull++. Choose 3 under Parameters and Type I under Settings. Keep the default simulation settings.

1. The estimated parameters are [math]\displaystyle{ \hat{\beta }=1.1976, }[/math] [math]\displaystyle{ \hat{\lambda }=4.94E-03, }[/math] [math]\displaystyle{ \hat{q}=0.1344 }[/math] .
2. The failure number and instantaneous failure intensity are given in the following plots.
Parametric RDA N(T) plot.png
Parametric RDA Lambda(T) plot.png
3. The conditional reliability is plotted below.
Parametric RDA Cond R(T) plot.png
4. Using QCP, the failure number and instantaneous failure intensity are:
QCP N(T).png
QCP Lambda(T).png
Retrieved from "https://www.reliawiki.com/index.php?title=Template:Example:_Recurrent_Events_Data_Parameteric_Air-Condition_Example&oldid=20053"