Template:Example:CD-GLL Weibull: Difference between revisions
| Line 21: | Line 21: | ||
<br> | <br> | ||
<br> | <br> | ||
: | [[Image:CD_GLL_Example_4.gif|thumb|center|300px|]] | ||
The estimated model parameters are shown next. | The estimated model parameters are shown next. | ||
| Line 27: | Line 27: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
\widehat{\beta }=\ & 3.507277 \\ | |||
\widehat{{{\alpha }_{0}}}=\ & -1.377671 \\ | |||
\widehat{{{\alpha }_{1}}}=\ & 450.488282 \\ | |||
\widehat{{{\alpha }_{2}}}=\ & 1.981082 | |||
\end{align}</math> | \end{align}</math> | ||
Revision as of 18:06, 22 February 2012
CD GLL-Weibull Example
A sample of 18 units of an electronic component was subjected to temperature and voltage stresses. The temperature was initially set 100K and was then continuously increased to 200K over a period of 20 hours. The temperature was again increased at 120 hours to 300K over a 20 hours period as shown in the next figure.
The voltage was initially set 4V and was then increased continuously to 8V over a period of 10 hours. The voltage was again increased at 110 hours to 12V over a 10 hours period as shown in the next figure.
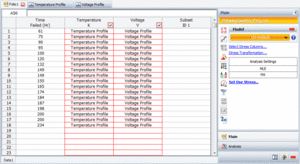
The failure times, as entered in ALTA, are shown in the next figure.
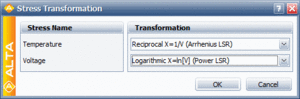
The stresses are transformed using an Arrhenius life-stress relationship for temperature, a Power Law life-stress reliationship for voltage and the Weibull distribution as the underlying distribution.
The estimated model parameters are shown next.
- [math]\displaystyle{ \begin{align} \widehat{\beta }=\ & 3.507277 \\ \widehat{{{\alpha }_{0}}}=\ & -1.377671 \\ \widehat{{{\alpha }_{1}}}=\ & 450.488282 \\ \widehat{{{\alpha }_{2}}}=\ & 1.981082 \end{align} }[/math]
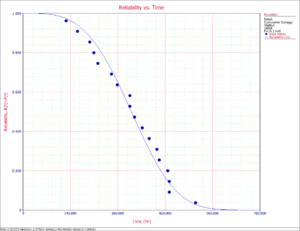
The use level (temperature = 100K, voltage = 4V) reliability plot is shown in the next figure.