ALTA ALTA Standard Folio Data IPL-Exponential: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Template:NoSkin}} | {{Template:NoSkin}} | ||
{| | {| class="FCK__ShowTableBorders" border="0" cellspacing="0" cellpadding="0" align="center"; style="width:100%;" | ||
|- | |- | ||
| valign="middle" align="left" bgcolor=EEEEEE|[[Image: Webnotes-alta.png |center|195px]] | |||
|} | |||
{| class="FCK__ShowTableBorders" border="0" cellspacing="1" cellpadding="1" | |||
|- | |- | ||
| | | valign="middle" |{{Font|Standard Folio Data IPL-Exponential|11|tahoma|bold|gray}} | ||
|- | |- | ||
| | | valign="middle" | {{Font|ALTA|10|tahoma|bold|gray}} | ||
|- | |- | ||
| | | valign="middle" | | ||
==IPL-Exponential== | ==IPL-Exponential== | ||
The IPL-exponential model can be derived by setting <math>m=L(V)</math> in Eqn. (inverse), yielding the following IPL-exponential <math>pdf</math> : | The IPL-exponential model can be derived by setting <math>m=L(V)</math> in Eqn. (inverse), yielding the following IPL-exponential <math>pdf</math> : | ||
<br> | <br> | ||
<math>f(t,V)=K{{V}^{n}}{{e}^{-K{{V}^{n}}t}}</math> | |||
<br> | <br> | ||
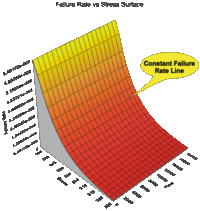
Note that this is a 2-parameter model. The failure rate (the parameter of the exponential distribution) of the model is simply <math>\lambda =K{{V}^{n}},</math> and is only a function of stress. | Note that this is a 2-parameter model. The failure rate (the parameter of the exponential distribution) of the model is simply <math>\lambda =K{{V}^{n}},</math> and is only a function of stress. | ||
<br> | <br> | ||
[[Image:ALTA8.4.gif| | [[Image:ALTA8.4.gif|200px|IPL-exponential failure rate function at different stress levels.]] | ||
|- | |- | ||
| | | valign="middle" | [http://reliawiki.com/index.php/Template:Ipl_exponential#IPL-Exponential IPL-Exponential] | ||
|} | |} | ||
Revision as of 21:57, 10 February 2012
| Standard Folio Data IPL-Exponential |
| ALTA |
IPL-ExponentialThe IPL-exponential model can be derived by setting [math]\displaystyle{ m=L(V) }[/math] in Eqn. (inverse), yielding the following IPL-exponential [math]\displaystyle{ pdf }[/math] :
|
| IPL-Exponential |